Identische Abbildung
Eine identische Abbildung oder Identität ist in der Mathematik eine Funktion, die genau ihr Argument zurückgibt. Obwohl sowohl die identische Abbildung als auch die Identitätsgleichung oft durch „Identität“ abgekürzt werden, handelt es sich um verschiedene Dinge.
Definition
Sei
eine Menge,
dann ist die identische Abbildung auf
definiert durch
das heißt, für jedes
aus
gilt
Die identische Abbildung ist somit eine Bijektion. Der Index wird oft
weggelassen, wenn die Definitionsmenge
aus dem Kontext hervorgeht. In diesem Fall wird auch
statt
geschrieben. Statt der Notation
wird manchmal die Schreibweise
,
mitunter auch nur
oder vor allem in der Funktionalanalysis
,
benutzt.
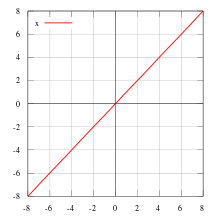
Der Graph der identischen Abbildung ist die Diagonale
Eigenschaften
Ist
eine beliebige Funktion, dann gilt für die Komposition
(Hintereinanderausführung) mit der Identität:
und
Daher ist in der Menge aller Funktionen von
nach
die Identität das neutrale
Element bezüglich der Komposition. Somit bilden diese Funktionen ein Monoid.
Insbesondere ist die Identität das neutrale Element in der Gruppe der Permutationen der Menge
.
Die Identität
auf der Menge der natürlichen
Zahlen ist eine multiplikative
Funktion, die in der Zahlentheorie
betrachtet wird.
Auf einem topologischen Raum ist die Identität eine stetige Funktion. Auf einem topologischen Vektorraum, zum Beispiel einem Banachraum, ist die Identität ein stetiger linearer Operator, der Einsoperator genannt wird. Ist der Banachraum zusätzlich endlichdimensional, so ist die Identität kompakt.
Die Matrizenmultiplikation mit der Einheitsmatrix (neutrales Element) ist eine Identitätsabbildung. In der linearen Algebra können Basiswechselmatrizen als Darstellungsmatrizen der identischen Abbildung bezüglich zweier unterschiedlicher Basen aufgefasst werden.
Die Existenz von Identitäten ist ein wesentlicher Bestandteil in der
Definition der Kategorie.
In den bekanntesten Fällen handelt es sich dabei um die identischen Abbildungen,
aber in der Kategorientheorie können die Identitäten auch abstraktere Objekte
sein. Aber auch dann werden die Bezeichnungen
oder
verwendet und es gelten die oben genannten Verknüpfungsregeln.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.07. 2021