Relation (Mathematik)
Eine Relation (lateinisch
relatio „Beziehung“,
„Verhältnis“) ist allgemein eine Beziehung, die zwischen Dingen bestehen kann.
Relationen im Sinne der Mathematik
sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob sie
bestehen oder nicht; Objekte können also nicht „bis zu einem gewissen Grade“ in
einer Relation zueinander stehen. Damit ist eine einfache mengentheoretische
Definition des Begriffs möglich: Eine Relation >
ist eine Menge von
-Tupeln.
In der Relation
zueinander stehende Dinge bilden
-Tupel,
die Element von
sind.
Wird nicht ausdrücklich etwas anderes angegeben, versteht man unter einer
Relation gemeinhin eine zweistellige oder binäre Relation. Bei
einer solchen Beziehung bilden dann jeweils zwei Elemente
und
ein geordnetes
Paar
Stammen dabei
und
aus verschiedenen Grundmengen
und
,
so heißt die Relation heterogen oder „Relation zwischen den Mengen
und
.“
Stimmen die Grundmengen überein (
),
dann heißt die Relation homogen oder „Relation in bzw. auf
der Menge
.“
Wichtige Spezialfälle, zum Beispiel Äquivalenzrelationen und Ordnungsrelationen, sind Relationen auf einer Menge.
Heute sehen manche Autoren den Begriff Relation nicht unbedingt als auf Mengen beschränkt an, sondern lassen jede aus geordneten Paaren bestehende Klasse als Relation gelten.
Definitionen
Zweistellige Relation
Eine zweistellige Relation
(auch binäre Relation genannt)
zwischen zwei Mengen
und
ist eine Teilmenge des kartesischen
Produkts
.
Die Menge
wird als Quellmenge (englisch: set of departure) der Relation
bezeichnet, die Menge
als Zielmenge (englisch: set of destination).
Manchmal ist diese Definition jedoch nicht präzise genug und man bezieht die
Quell- und Zielmenge in die Definition mit ein, obige Teilmenge wird dann der
Graph (seltener
Graf)
der Relation genannt. Eine zweistellige Relation
ist dann definiert als Tripel
mit
.
Die Kenntnis von Quelle und Zielmenge ist insbesondere dann von Bedeutung, wenn man Funktionen als spezielle (sogenannte funktionale) Relationen betrachtet.
Als Urbild-, Argument- oder Definitions- oder
Vorbereich
einer gegebenen zweistelligen Relation
wird der kleinstmögliche Vorbereich zum Graphen
verstanden, dessen Elemente alle in den geordneten Paaren von
tatsächlich auf der linken Seite auftreten, in Zeichen
.[1]
Der Wertevorrat, Werte- oder Bild- oder Nachbereich
bezeichnet in diesem Sinne den kleinsten Nachbereich zu
bei gegebenem
,
dessen Elemente also alle in den Paaren von
auf der rechten Seite auftreten, in Zeichen
.[2]
Gelegentlich wird für die Vereinigungsmenge die Bezeichnung Feld (oder Knotenmenge) benutzt, in Zeichen
.
Darüber hinaus finden sich folgende Bezeichnungen:
- Domäne (englisch domain)
entweder für die (im Prinzip beliebig große) Quellmenge oder für die (durch den Graphen festgelegte) Urbildmenge (Definitionsbereich),
- Co-Domäne (englisch codomain, range)
entweder für die Zielmenge oder für die Bildmenge,[3]
- Knotenmenge (
) für das Feld einer Relation.
Stimmen zwei Relationen in ihren Graphen überein, so sagt man auch, sie seien
im Wesentlichen gleich.
Beispiel: Jede Relation
ist im Wesentlichen gleich mit
und mit der homogenen
Relation
.
n-stellige Relation
Allgemeiner ist eine -stellige
Relation
eine Teilmenge des kartesischen Produkts von
Mengen
mit
.
Dabei bezeichnet
die endliche
Folge der Mengen, und
das kartesische Produkt.
Die ausführlichere Definition lässt sich auch auf -stellige
Relationen verallgemeinern und man erhält dann das
-Tupel
mit
.
Die Mengen
heißen Trägermengen der Relation mit den minimalen Trägermengen zum
Graphen
,
nämlich
.
Das Feld einer -stelligen
Relation ist gegeben durch
.
Wesentliche Gleichheit ist analog definiert wie für zweistellige Relationen
durch Übereinstimmung der Graphen, insbesondere ist jede -stellige
Relation
im Wesentlichen gleich mit
und mit der homogenen Relation
.
- Einstellige und nullstellige Relation
Eine einstellige Relation auf einer Menge
ist somit einfach eine Teilmenge
,
in der ausführlichen Definition
mit
.
Die nullstelligen Relationen sind demnach die Teilmengen des leeren
kartesischen Produkts
bzw.
,
also
und
,
ausführlich
und
.
Relationen zwischen oder auf echten Klassen
Häufig sind die Trägerbereiche
einer Relation keine Mengen, sondern echte Klassen, man spricht
dann von Klassenrelationen. Gelegentlich kann man mengentheoretische Probleme,
die sich daraus ergeben, vermeiden, indem man nur noch den Graph der
entsprechenden Relation betrachtet. Die (minimalen) Trägermengen (
,
im zweistelligen Fall Definitions- und Wertemenge
)
sind tatsächlich Mengen, aber es ist nicht nötig, sich von vornherein auf
Quellmenge, Zielmenge, … (
)
festzulegen, wenn die Relationen im Wesentlichen gleich sind. Nicht immer ist
das möglich, beispielsweise für die Äquivalenzrelation der Gleichmächtigkeit,
siehe auch: Kardinalzahlen
§Definition. Gleichheit von Relationen im Wesentlichen ist ein weiteres
Beispiel.
Eine zweistellige Klassenrelation
mit Quellklasse
und Zielklasse
heißt vorgängerklein,[4]
wenn für alle
die Klasse der Vorgänger
(Urbildfaser von
,
s.u.) eine Menge (d.h. keine echte Klasse) ist.
Die Relation heißt englisch right-narrow (deutsch in etwa
nachfolgerklein),
wenn für alle
die Klasse der Nachfolger
(Bildfaser von
)
eine Menge ist. Im Fall der Rechtseindeutigkeit (partielle Abbildungen,
Abbildungen, s.u.) ist eine Klassenrelation stets klein, da es zu jedem
Urbild (genau oder höchstens) einen Bildwert gibt, die Klasse der Nachfolger
also eine Einermenge
(oder die Leermenge)
ist. Jede injektive Klassenabbildung ist beides, klein und vorgängerklein. Die
Enthaltenseinsrelation
ist für jede Klasse
vorgängerklein, da die
keine echten Klassen sein können, sondern Mengen sind und damit
ebenfalls eine Menge ist.[5]
Die Begriffe Vorgänger und Nachfolger selbst werden üblicherweise
im Kontext von Ordnungsrelationen verwendet, siehe Ordnungsrelation
§Vorgänger und Nachfolger.
Erläuterungen und Schreibweisen
Das kartesische
Produkt zweier Mengen
und
ist die Menge aller geordneten
Paare von
und
wobei
irgendein Element aus der Menge
und
eines aus
darstellt. Bei dem geordneten Paar ist die Reihenfolge wichtig, d.h.
unterscheidet sich von
im Gegensatz zum ungeordneten
Paar
das identisch ist mit
Für
schreibt man auch
,
um zu verdeutlichen, dass jene Beziehung zwischen den Objekten besteht
(wie in
).
Die Leermenge als Teilmenge des
kartesischen Mengenprodukts als Relation aufgefasst heißt Nullrelation
,
das volle Produkt heißt Allrelation (auch Universalrelation)
(auch als
bezeichnet).[6]
Relationen und Funktionen
- Eine Funktion
ist eine spezielle, nämlich eine linkstotale und rechtseindeutige (zweistellige) Relation, näheres siehe unten.
- Eine Multifunktion
ist eine linkstotale Relation
.
- Eine partielle
Funktion
ist eine (im Allgemeinen nicht linkstotale) rechtseindeutige Relation
.
In allen Fällen ist
(beziehungsweise
wenn die ausführliche Definition zugrundegelegt wird).
Für Funktionen und Multifunktionen gilt:
- Bei der ausführlicheren Definition
kann, weil
durch
eindeutig bestimmt ist (linkstotal), auch
weggelassen und einfacher
genommen werden.
Für Funktionen und partielle Funktionen gilt:
- Für
bzw.
wird auch
(englisch: maplet), oder
geschrieben.
Allgemein gilt:
- Die nullstelligen Relationen
(als nullstellige Nullrelation) und
(als nullstellige Vollrelation) haben als charakteristische Funktionen die booleschen oder logischen Konstanten
und
, wie immer für Nullrelation und Allrelation.
- Der Fall einstelliger Relationen ist trivial.
- Eine Relation
(bzw.
) entspricht auf eindeutige Weise einer Wahrheitsfunktion
. Diese Funktion ist auch als Indikatorfunktion oder charakteristische Funktion der Teilmenge
(bzw.
) bekannt, wobei
durch
ersetzbar ist.
- Eine
-stellige Relation
(bzw.
) entspricht der charakteristischen Funktion
Es gilt:
.
.
.
.[7]
- Eine Relation
lässt sich ebenso als eine Abbildung
von
in die Potenzmenge von
auffassen,
man spricht dann oft von einer Korrespondenz, und für
von einer Transitionsrelation.
Verkettung von Relationen
Die Vorwärtsverkettung
zweier zweistelliger Relationen
ist wie folgt definiert:
Die Verkettung in der umgekehrten Reihenfolge wird als Rückwärtsverkettung bezeichnet:
.
Manche Autoren (W. v.O.Quine) verwenden hierfür alternativ
die Notation .
Die Reihenfolge ist bei der Rückwärtsverkettung dieselbe wie bei der Verkettung von Funktionen (die als spezielle Relationen aufgefasst werden können).
Die Verkettung zweistelliger Relationen wird auch als relatives
Produkt bezeichnet. Bei der Verkettung kann auch die einfachste Relation,
die in jedem kartesischen Produkt enthaltene leere Relation
(leere
Menge) auftreten, nämlich wenn
und
disjunkt
sind, in Zeichen:
.
Beispiel: Die Relation „Schwägerin sein von“ ist die Vereinigungsmenge
- des relativen Produktes der Relation „Bruder sein von“ und der Relation „Ehefrau sein von“ und
- des relativen Produktes der Relation „Ehepartner(in) sein von“ und der Relation „Schwester sein von“.
Umkehrrelation
Die Umkehrrelation (auch konverse Relation, Konverse
oder inverse Relation genannt) ist für eine zweistellige Relation
definiert als
.
Gelegentlich findet sich hierfür auch die Bezeichnung transponierte
Relation, in Zeichen .
- Beispiel 1: Die Umkehrrelation der Relation „ist Nachkomme von“ ist die Relation „ist Vorfahre von“.
- Beispiel 2: Die Umkehrrelation der Relation „ist kleiner als“ ist die Relation „ist größer als“.
- Beispiel 3: Die Umkehrrelation der Relation „liefert an“ ist die Relation „wird beliefert von“.
Die Verallgemeinerung der Umkehrrelation (Konverse) auf -stellige
Relationen ist die Permutation
der Koordinaten der in ihr enthaltenen
-Tupel,
speziell
- die Vertauschungen von lediglich 2 Koordinaten (Transpositionen) und
- die Umkehrung der Reihenfolge (Spiegelung),
beides Beispiele (zyklischer) selbstinverser Permutationen.
Sei
eine Permutation (d.h. eine bijektive Abbildung von
auf sich selbst),[9]
und sei
eine
-stellige
Relation, dann ist
die nach Anwenden der Permutation
sich ergebende Relation (man verstehe
als Familie).
Im Fall der Spiegelung
ist .
Bild und Urbild
Bei einer zweistelligen Relation
bezeichnet man als das Bild einer Menge oder Klasse
die Menge bzw. Klasse
.
Das Urbild einer Menge oder Klasse
ist die Menge bzw. Klasse
Gelegentlich findet sich hierfür auch die Bezeichnung
(sic!),
oft auch mit eckigen Klammern als
notiert. Bei Korrespondenzen
ist für die Bildfaser einer Einermenge
(Singleton)
auch die Schreibweise
im Gebrauch, wofür teilweise ebenfalls die Notation mit eckigen Klammern
verwendet wird, d.h.
;
im Fall symmetrischer Relationen, d.h. (ggf. partieller) Äquivalenz- bzw.
Verträglichkeitsrelationen ist die Notation
und spricht von Äquivalenz- bzw. Verträglichkeits- oder Toleranzklassen.
Einschränkung
Relationen lassen sich auf verschiedene Art und Weise auf Teilmengen der Trägermengen einschränken, Näheres siehe Einschränkung einer Relation.
Komplementäre Relation
Für zweistellige Relationen
bei festem Vor- und Nachbereich
ist die komplementäre Relation gegeben durch
,
analog für -stellige
Relationen
bei festen Trägerbereichen
.
Auf den reellen Zahlen
ist beispielsweise
die komplementäre Relation zu
.
Wird die komplexe Notation
zugrunde gelegt, so ist
,
wobei
jetzt keine äußeren Zugaben mehr sind, sondern Bestandteile der Relation; analog
für
-stellige
Relationen in dieser Notation.
Wie für alle Mengen ist das Komplement auch für Relationen involutiv:
.
Homogene Relationen
Ist ,
also
,
dann nennt man die Relation homogen. Manche Autoren definieren eine
allgemeine Relation bereits als homogene Relation, denn eine allgemeine Relation
kann immer auch als Einschränkung einer homogenen betrachtet werden:
.
Spezielle homogene Relationen und Operationen auf homogenen Relationen
Eine spezielle homogene Relation in einer Menge
ist die Gleichheits- oder Identitätsrelation oder Diagonale
Alternative Notationen für die Diagonale sind
oder
;
wenn
bereits bekannt ist, wird sie einfach mit
,
oder
bezeichnet.[12]
Eine weitere spezielle homogene Relation ist die Allrelation oder Universalrelation
(auch mit Nabla als
bezeichnet).
Wenn
bereits bekannt ist, wird wie bei der Identitätsrelation auch hier der Index
weggelassen.[13]
Die Allrelation spielt eine Rolle in der Graphentheorie (siehe unten). Ein Anwendungsbeispiel ist folgender Satz:
- Ist
ein gerichteter Graph mit einer Menge
von Ecken und einer (assoziierten) Relation
von Kanten, so ist
genau dann (stark) zusammenhängend, wenn die reflexiv-transitive Hülle von
die Universalrelation ist.
Die Bildung der Umkehrrelation (konversen Relation) einer homogenen zweistelligen Relation liefert wieder eine homogene zweistellige Relation (Abgeschlossenheit), zweimalige Ausführung ergibt wieder die Ausgangsrelation (Involutivität). Die Verknüpfung einer beliebigen (auch nicht-homogenen) Relation mit der dazu konversen Relation ist symmetrisch und reflexiv, also eine Äquivalenzrelation, aber im Allgemeinen nicht gleich der Identitätsrelation.
Im Fall einer homogenen Relation
ist die Verkettung
ebenfalls eine homogene Relation, sodass die homogenen Relationen in
ein Monoid mit
der multiplikativen
Verknüpfung
und dem neutralen
Element
bilden. Somit kann
und können allgemeiner Potenzen
für
definiert werden, wobei
ist.[14]
wird daher auch Einsrelation auf der Menge
genannt.
In Erweiterung der Notation
anstelle von
für die Umkehrrelation bezeichnet man deren Potenzen mit negativen
Exponenten:
.
Damit sind beliebige ganze Zahlen
als Exponent zulässig.
Zudem besitzt jedes Monoid homogener Relationen mit der leeren Relation (Nullrelation)
noch ein absorbierendes Element.
Durch Vereinigung der verschiedenen Potenzen entstehen die Relationen[15]
und
.
Algebraische Strukturen
Alles zusammengefasst, bilden die zweistelligen Relationen auf einer Menge
eine Relationsalgebra
Unter Verwendung der Notationen .[16]
Zusammen mit den Beschränkungen bilden die homogenen Relationen eine (heterogene) Peirce-Algebra.
Homogene mehrstellige Relationen
Homogene mehrstellige Relationen sind (mit ihrem Graphen) Teilmengen von
.
Für festes
sind die Allrelation
(auch
)
und die Identitätsrelation (Diagonale)
(auch
)
gegeben durch
.
Die als Verallgemeinerung der Konversenbildung beschriebene Anwendung von
Permutationen auf ihre -Tupel
sind hier von besonderer Bedeutung, da man auf diese Weise immer innerhalb der
Teilmengen von
bleibt (Abgeschlossenheit). M.a.W. sind diese Operationen
bijektive Abbildungen in
.
Auch weitere von zweistelligen Relationen bekannte Begriffe wie Reflexivität und
Symmetrie etc. lassen sich in kanonischer (natürlicher) Weise auf beliebig
mehrstellige Relationen ausdehnen.
Graphentheorie und Verallgemeinerungen
Die Graphentheorie beschreibt Mengen mit einer Relation darauf zusammen mit gewissen Verallgemeinerungen unter einem gemeinsamen Oberbegriff, dem Graphen.[17] Die in der Graphentheorie betrachteten Fälle sind (wenn nicht anders angegeben) üblicherweise endlich (finit).
1. Eine relationale
Struktur
bestehend aus einer Menge
zusammen mit einer Relation
darauf wird als gerichteter (auch orientierter) Graph
bezeichnet.
wird Knotenmenge des Graphen genannt, ihre Elemente heißen Knoten.
wird als Teilmenge von
als Kantenmenge bezeichnet, ihre Elemente (geordnete Paare aus
)
heißen gerichtete (d.h. orientierte) Kanten.
2. Symmetrische Graphen ,
d.h. Mengen
mit einer symmetrischen Relation
,
sind äquivalent einem ungerichteten Graphen
,
dessen Kantenmenge
aus (ungerichteten) Kanten, nämlch den (ungeordnete) Mengen
mit
(hier äquivalent zu
)
besteht.
3. Weitere Verallgemeinerungen betreffen sogenannte gerichtete Graphen mit
zusammengefassten Mehrfachkanten, bei denen jede Kante eine natürliche Zahl
als Multiplizität hat. Die Kanten solcher Graphen können durch eine Multimenge
dargestellt werden: eine Abbildung
mit einer Menge
und einer Abbildung
,
die jedem Knoten
eine Farbe genannte positive Zahl
zuordnet. Ähnlich sind Graphen mit gefärbte
Knoten und/oder Kanten.[18]
4. Von gewichteten
Knoten und/oder Kanten: Von Gewichten anstelle von Farben spricht man, wenn die
Abbildung
reellwertig ist. Bei
gewichteten Knoten entspricht dies einer Fuzzymenge
,
bei
ist
ein real valued multiset.
Entsprechendes gilt für gewichtete Kanten. Für orientierte Graphen bedeutet
dies insbesondere, dass die Kantenmenge (eine Relation, d.h. Menge
geordneter Knotenpaare) in einer Erweiterung des Relationsbegriffs zu einer
Multimenge oder Fuzzymenge wird.
Beispiele
-
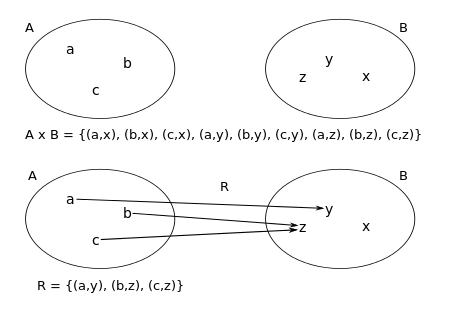 Alle möglichen geordneten Paare
Alle möglichen geordneten Paaremit
und
sowie eine zwischen
und
definierte Relation
-
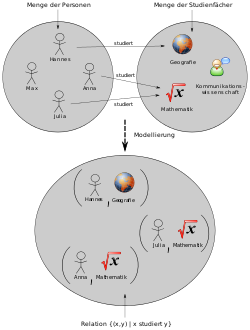 Beispiel einer Relation „Eine Person x studiert das Fach y“.
Beispiel einer Relation „Eine Person x studiert das Fach y“. -
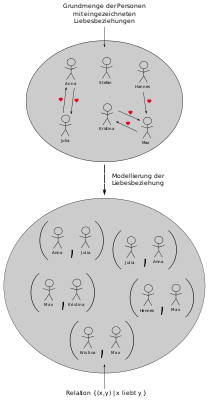 Beispiel einer Relation „Person x liebt Person y“. Diese zweistellige Relation wird über eine Menge von geordneten Paaren modelliert.
Beispiel einer Relation „Person x liebt Person y“. Diese zweistellige Relation wird über eine Menge von geordneten Paaren modelliert. -
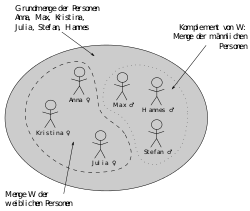 Die einstellige Relation „Person x ist weiblich“ wird als Teilmenge der Grundmenge modelliert.
Die einstellige Relation „Person x ist weiblich“ wird als Teilmenge der Grundmenge modelliert. -
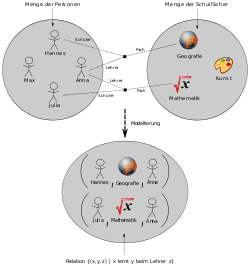 Die dreistellige Relation „Person x lernt das Fach y beim Lehrer z“ wird über eine Menge von 3-Tupeln realisiert.
Die dreistellige Relation „Person x lernt das Fach y beim Lehrer z“ wird über eine Menge von 3-Tupeln realisiert.
Eigenschaften zweistelliger Relationen
Allgemeine Relationen
Übersicht über die Eigenschafte
Die folgenden Relationen sind für Funktionen (dargestellt als spezielle
Relationen) wichtig. Im Allgemeinen besteht hier die Relation
zwischen zwei verschiedenen Mengen
der Fall
ist natürlich auch möglich.
| Die Relation |
genau dann, wenn (Prädikatenlogik) | oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| linkstotal bzw. definal (Multifunktion) |
Jedes Element aus | ||
| rechtstotal bzw. surjektiv | Jedes Element aus | ||
| linkseindeutig bzw. injektiv | Jedes Element aus | ||
| (rechts-) eindeutig (partielle Funktion) |
Jedes Element aus |
| Die Relation |
genau dann, wenn (Prädikatenlogik) | oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| bitotal | Jedes Element aus | ||
| eineindeutig | Jedes Element aus | ||
| bijektiv | Jedes Element aus | ||
| Abbildung bzw. Funktion | Jedes Element aus |
Alternative Sprechweisen
Man sagt auch
- linksvollständig an Stelle von linkstotal,
- rechtsvollständig an Stelle von rechtstotal,
- voreindeutig an Stelle von linkseindeutig,
- nacheindeutig an Stelle von rechtseindeutig,
Eine rechtseindeutige bzw. funktionale Relation nennt man auch partielle Funktion. Wenn diese auch linkstotal – also eine Funktion – ist, dann sagt man zur Verdeutlichung auch totale Funktion.
Funktionen
Übersicht über Funktionseigenschaften bei Relationen
Eine Relation ist also genau dann eine (totale) Funktion, wenn sie linkstotal
und rechtseindeutig ist. Das heißt, dass jedes Element in A genau einen Partner
in B hat. Die Eigenschaften surjektiv, injektiv und bijektiv werden in der Regel
für Funktionen gebraucht und spezifizieren bestimmte zusätzliche Eigenschaften.
Z.B. ist eine Funktion (und auch eine beliebige Relation)
genau dann bijektiv, wenn sie surjektiv und injektiv ist, also wenn ihre
Umkehrrelation
eine Funktion ist.
| Die Relation |
genau dann, wenn sie eine | ist oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| Surjektion | surjektive Funktion | Jedes Element aus | |
| Injektion | injektive Funktion | Jedes Element aus | |
| Bijektion | bijektive Funktion | Jedes Element aus |
Umkehrfunktion
Eine Abbildung bzw. Funktion nennt man auch
- umkehrbar eindeutig oder umkehrbar, falls sie bijektiv ist.
Eine Funktion ist als Relation immer umkehrbar, als Funktion ist sie dagegen genau dann umkehrbar, wenn ihre Umkehrrelation auch wieder eine Funktion ist, also wenn es eine Umkehrfunktion von ihr gibt.
Homogene Relationen
Die in den folgenden Tabellen gegebenen Beispiele beziehen sich bei Verwendung von Gleichheitszeichen „=“, Kleinerzeichen „<“ und Kleinergleich-Zeichen „≤“ auf die gewöhnliche Anordnung reeller Zahlen.
| Die Relation |
genau dann, wenn (Prädikatenlogik) | oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| rechtskomparativ bzw. drittengleich | Stehen zwei Elemente jeweils zu einem gleichen dritten Element in
Relation, dann stehen auch sie zueinander in Relation. Z.B. gilt mit
| ||
| linkskomparativ bzw. euklidisch | Steht ein erstes Element jeweils zu einem zweiten und zu einem dritten
Element in Relation, so stehen auch diese zueinander in Relation.
Z.B. gilt mit | ||
| transitiv | Steht ein erstes Element zu einem zweiten Element und dieses wiederum
zu einem dritten Element in Relation, so steht auch das erste Element zum
dritten Element in Relation. Z.B. folgt aus | ||
| intransitiv | Stehen zwei Elemente in Relation und zudem das zweite Element zu einem
dritten Element in Relation, dann steht das erste Element zum dritten
Element nicht in Relation. Z.B. ist jede natürliche
Zahl |
Nichttransitivität (d.h. die Relation ist nicht transitiv), Intransitivität und negative Transitivität sind jeweils voneinander verschieden.
| Die Relation |
genau dann, wenn (Prädikatenlogik) | oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| reflexiv | Jedes Element steht in Relation zu sich selbst, z.B.
ist stets | ||
| irreflexiv | Kein Element steht in Relation zu sich selbst, z.B. gilt |
| Die Relation |
genau dann, wenn (Prädikatenlogik) | oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| symmetrisch | Die Relation ist ungerichtet, z.B. folgt aus | ||
| antisymmetrisch bzw. identitiv | Es gibt keine zwei verschiedenen Elemente, die in beiden Richtungen in
Relation stehen, z.B. folgt aus | ||
| asymmetrisch | Es gibt keine zwei Elemente, die in beiden Richtungen in Relation
stehen, z.B. folgt aus |
| Die Relation |
genau dann, wenn (Prädikatenlogik) | oder gleichwertig (Mengenschreibweise) | und das bedeutet: |
|---|---|---|---|
| total bzw. vollständig | Je zwei Elemente stehen in Relation, z.B. wenn stets | ||
| konnex[19] bzw. verbunden | Je zwei verschiedene Elemente stehen in Relation, z.B. wenn
stets | ||
| trichotom | Je zwei verschiedene Elemente stehen stets auf genau eine Weise in
Relation, z.B. wenn stets entweder |
Zwischen den Eigenschaften gelten folgende Zusammenhänge:
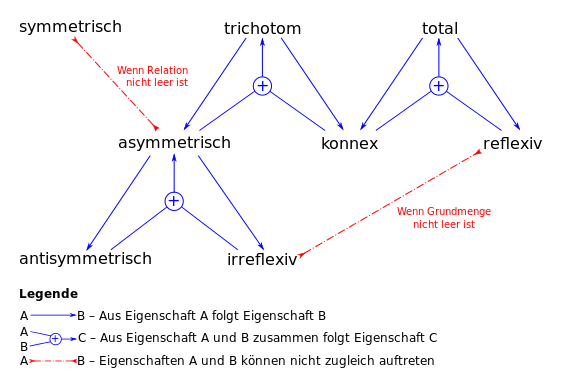
Zwischen den Eigenschaften einer Relation
und denen ihres Komplements
bestehen folgende Zusammenhänge:
ist reflexiv
ist irreflexiv (und umgekehrt).
ist symmetrisch
ist symmetrisch.
ist antisymmetrisch
ist konnex (und umgekehrt).
ist total
ist asymmetrisch (und umgekehrt).[20]
Klassen von Relationen
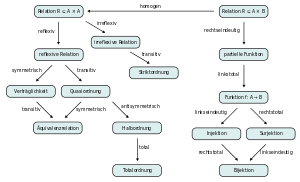
Weitere wichtige Klassen von Relationen und ihre Eigenschaften:
- Quasiordnung oder Präordnung: transitiv und reflexiv
- Verträglichkeitsrelation oder Toleranzrelation: verträglich (reflexiv und symmetrisch) (englisch: im finiten Fall dependency relation, im transfiniten Fall tolerance relation).
- Äquivalenzrelation: transitiv, reflexiv und symmetrisch
- Halbordnung/Teilordnung, partielle Ordnung oder Ordnung: transitiv, reflexiv und antisymmetrisch.
- Vollordnung/Totalordnung oder lineare Ordnung: transitiv, reflexiv, antisymmetrisch und total
- Wohlordnung: eine lineare Ordnung, in der jede nichtleere Teilmenge von A ein kleinstes Element besitzt
- Striktordnung oder strenge Halbordnung/Teilordnung: transitiv, irreflexiv und antisymmetrisch (d.h. asymmetrisch)
- Strenge Vollordnung/Totalordnung oder lineare Striktordnung: transitiv, irreflexiv, antisymmetrisch und konnex
Relationszeichen
In der elementaren Mathematik gibt es drei grundlegende Vergleichsrelationen:
(Beispiel:
„2 ist kleiner als 3“)
(Beispiel:
„3 ist gleich 3“)
(Beispiel:
„3 ist größer als 2“)
mit .
Zwei reelle Zahlen stehen immer in genau einer dieser Relationen zueinander. Mit diesen Relationszeichen lassen sich auch weitere bilden. Es gilt:
, falls
oder
(Beispiel:
„4 ist nicht größer als 5“)
, falls
oder
(Beispiel:
„5 ist nicht kleiner als 5“)
, falls
oder
(Beispiel:
„4 ist nicht gleich 5“)
für alle .
Für komplexe Zahlen existieren obige Ordnungsrelationen nicht.
Mathematiker verwenden das Zeichen ≤ auch für abstrakte Ordnungsrelationen (und ≥ für die zugehörige Umkehrrelation) während „<“ keine Ordnungsrelation im Sinne der mathematischen Definition ist.
Für Äquivalenzrelationen werden „symmetrische“ Symbole wie ≈, ~, ≡ bevorzugt.
Kategorientheorie
Für einen beliebigen Halbring
mit Nullelement
und Einselement
ist folgendes
eine Kategorie:
.
- Ein Morphismus
ist eine Funktion
.
- Für Objekte
gilt
.
- Das ist identisch mit dem Kronecker-Delta:
.
- Für Objekte
und Morphismen
gilt
.
Die Morphismen sind also mengenindizierte Matrizen und ihre Komposition
geschieht wie bei der Matrixmultiplikation,
entspricht der Einheitsmatrix
.
Im Sonderfall
gilt
,
d.h.,
ist die Kategorie der Relationen.
Anwendung
Operationen auf ganzen Relationen werden in der relationalen Algebra untersucht. In der Informatik sind Relationen bei der Arbeit mit relationalen Datenbanken wichtig.
Siehe auch
Literatur
- Stefan Brass: Mathematische Logik mit
Datenbank-Anwendungen. Martin-Luther-Universität Halle-Wittenberg,
Institut für Informatik, Halle 2005, S. 176
(
 informatik.uni-halle.de [PDF]).
informatik.uni-halle.de [PDF]). - Marcel Erné: Einführung in die Ordnungstheorie. Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8.
- H. König: Entwurf und Strukturtheorie von Steuerungen für Fertigungseinrichtungen (= ISW Forschung und Praxis. Band 13). Springer, Berlin/Heidelberg 1976, ISBN 3-540-07669-7.
- Ingmar Lehmann, Wolfgang Schulz: Mengen – Relationen – Funktionen. Eine anschauliche Einführung. 3., überarbeitete und erweiterte Auflage. Vieweg+Teubner, Wiesbaden 2007, ISBN 978-3-8351-0162-3.
- Willard van Orman Quine: Mengenlehre und ihre Logik (= Logik und Grundlagen der Mathematik. Band 10). Vieweg+Teubner, Wiesbaden 1973, ISBN 3-528-08294-1, S. 264 (amerikanisches Englisch: Set Theory And Its Logic. Cambridge, MA 1963. Ullstein 1978 als Taschenbuch).
- Fritz Reinhardt, Heinrich Soeder: dtv-Atlas Mathematik. 11. Auflage. Band 1: Grundlagen, Algebra und Geometrie. Deutscher Taschenbuchverlag, München 1998, ISBN 3-423-03007-0.
Anmerkungen
- ↑
Weitere Bezeichnungsweisen:
, in der englischsprachigen Literatur:
- ↑
Weitere Bezeichnungsweisen:
, in der englischsprachigen Literatur:
,
- ↑ In der Theorie algebraischer Strukturen benutzt man – besonders im Hinblick auf die Kategorientheorie die Begriffe domain und codomain meist im Sinn von Quell- und Zielmenge, während in einführenden Schriften zur Mengenlehre diese meist als Urbild- und Bildmenge definiert werden,
- ↑ auch mengenähnlich, mengenartig, auf engl.: left-narrow bzw. set-like genannt,
- ↑
Falls Urelemente
zugelassen sind: für Urelemente
ist
, ebenfalls eine Menge.
- ↑
Im allgemeinen Fall mit der Trägermengensequenz
ist die Allrelation
, im homogenen Fall mit der n-fachen Trägermenge
ist
.
- ↑ Die charakteristische Funktion als Wahrheitsfunktion entspricht daher einem logischen Prädikat, und in der Modelltheorie nennt man die Relationssymbole deswegen auch Prädikatsymbole, siehe Stefan Brass (2005) S. 16.
- ↑
Gelegentlich findet sich auch der Strichpunkt in
Konturdarstellung.
wird in Wikipedia aber hardware- und einstellungsabhängig nicht immer korrekt dargestellt.
- ↑
Als Bijektion auch mit
notiert.
- ↑
Zur Notation
siehe Gary Hardegree: Set Theory, Chapter 2: Relations, University of Massachusetts, Amherst, Department of Philosophy, Herbst 2015, S. 11: D16 und D17. Im Gegensatz zu den anderen Notationen referenzieren diese Symbole Abbildungen (Funktionen) zwischen den Potenzmengen
.
- ↑ Bei Ordnungsrelationen und ähnlichen sprechen manche Autoren auch von Vorgängermenge oder -klasse, siehe Heike Mildenberger 2015, S. 6, Definition 1.12.
- ↑
Der obigen ausführlichen Relationsdefinition
folgend wird man die Diagonale als den Graphen der Identität verstehen:
(Relation) mit
(Graph).
- ↑
Der obigen ausführlichen Relationsdefinition
folgend wird man in Analogie zur Diagonalen das Nabla als den Graphen der
Allrelation verstehen:
(Relation) mit
(Graph)
- ↑
Das kann zu Verwechslungen mit dem kartesischen
Produkt
mit
führen. Die Bedeutung ergibt sich jeweils aus dem Sinnzusammenhang.
- ↑ Siehe dazu auch: Kleenesche Hülle.
- ↑
Von den Verknüpfungen
(einstellig) sowie
(zweistellig) sind – genau genommen – die Einschränkungen auf
bzw.
gemeint.
- ↑ Der Begriff Graph im graphentheoretischen Sinn ist zu unterscheiden vom Begriff Graph einer Relation entsprechend der eingangs erwähnten ausführlichen Definition von Relationen (wie auch Abbildungen), welche in der Graphentheorie nicht verwendet wird.
- ↑
Der Begriff Farbe rührt daher, dass man die
entsprechend der Multimengentheorie als Multiplizität verstandene Zahl
in der bildlichen Darstellung als nummerncodierte Farbe der Kante
wiedergibt, analog bei gefärbten Knoten
.
Ein Beispiel für Farbnummern wären etwa die RAL-Farben. - ↑ Nicht selten wird konnex auch wie total definiert.
- ↑
Man erkennt dies leicht anhand der obigen
Tabellen (1. und 2. Spalte) unter Berücksichtigung von
, d.h.
und der prädikatenlogischen Regeln. Die Umkehrungen gelten wegen Involutivität
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.04. 2024