Reflexive Relation

Drei reflexive Relationen, als gerichtete Graphen dargestellt

Die Reflexivität einer zweistelligen Relation R auf einer Menge ist gegeben, wenn x R x für alle Elemente x der Menge gilt (also jedes Element in Relation zu sich selbst steht). Man nennt R dann reflexiv. Die Relation heißt irreflexiv, wenn die Beziehung x R x für kein Element x der Menge gilt (also kein Element in Relation zu sich selbst steht). Es gibt Relationen, die weder reflexiv noch irreflexiv sind.

Die Reflexivität ist eine der Voraussetzungen für eine Äquivalenzrelation oder eine Ordnungsrelation; die Irreflexivität ist eine der Voraussetzungen für eine strikte Ordnungsrelation.

Formale Definition

Ist eine Menge und $R\subseteq M\times M$ eine zweistellige Relation auf , dann definiert man (unter Verwendung der Infixnotation):

ist reflexiv : $\Longleftrightarrow \forall x\in M:xRx$

ist irreflexiv : $\Longleftrightarrow \forall x\in M:\neg \ xRx$

Beispiele

Reflexiv

Die Kleiner-Gleich-Relation $\leq \$ auf den reellen Zahlen ist reflexiv, da stets $x\leq x$ gilt. Sie ist darüber hinaus eine Totalordnung. Gleiches gilt für die Relation $\geq \$ .

Die gewöhnliche Gleichheit $=\$ auf den reellen Zahlen ist reflexiv, da stets gilt. Sie ist darüber hinaus eine Äquivalenzrelation.

Die Teilmengenbeziehung $\subseteq$ zwischen Mengen ist reflexiv, da stets $A\subseteq A$ gilt. Sie ist darüber hinaus eine Halbordnung.

Irreflexiv

Die Kleiner-Relation $<\$ auf den reellen Zahlen ist irreflexiv, da nie gilt. Sie ist darüber hinaus eine strenge Totalordnung. Gleiches gilt für die Relation $>\$ .

Die Ungleichheit $\neq$ auf den reellen Zahlen ist irreflexiv, da nie $x\neq x$ gilt.

Die echte Teilmengenbeziehung $\subset$ zwischen Mengen ist irreflexiv, da nie $A\subset A$ gilt. Sie ist darüber hinaus eine strenge Halbordnung.

Weder reflexiv noch irreflexiv

Die folgende Relation auf der Menge der reellen Zahlen ist weder reflexiv noch irreflexiv:
$xRy:\Longleftrightarrow y=x^{2}$
(Begründung: Für gilt , für gilt $\neg xRx$ .)

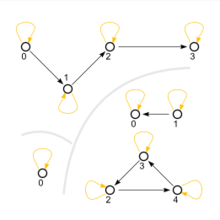
Darstellung als gerichteter Graph

Jede beliebige Relation auf einer Menge kann als gerichteter Graph aufgefasst werden (Beispiel siehe oben). Die Knoten des Graphen sind dabei die Elemente von . Vom Knoten zum Knoten wird genau dann eine gerichtete Kante (ein Pfeil $a\longrightarrow b$ ) gezogen, wenn $aRb\$ gilt.

Die Reflexivität von lässt sich im Graphen nun so charakterisieren: Für jeden Knoten gibt es eine Schleife ${\stackrel {a}\circlearrowright }$ . Entsprechend ist die Irreflexivität dadurch gegeben, dass es für keinen Knoten eine Schleife ${\stackrel {a}\circlearrowright }$ gibt.

Eigenschaften

Mit Hilfe der identischen Relation $Id_{M}$ (die aus allen Paaren besteht) kann man die Begriffe auch so charakterisieren:

ist reflexiv $\Longleftrightarrow Id_{M}\subseteq R$

ist irreflexiv $\Longleftrightarrow Id_{M}\cap R=\varnothing$

Ist die Relation reflexiv bzw. irreflexiv, dann gilt dies auch für die konverse Relation $R^{-1}$ . Beispiele: die zu $\leq$ konverse Relation ist $\geq$ , die zu $<\$ konverse ist $>\$ .

Ist die Relation reflexiv, dann ist die komplementäre Relation $R^{{{\rm {c}}}}$ irreflexiv. Ist irreflexiv, dann ist $R^{{{\rm {c}}}}$ reflexiv. Dabei ist die komplementäre Relation definiert durch

$xR^{{{\rm {c}}}}y:\Longleftrightarrow \neg xRy$ .

Die Relation auf der leeren Menge ist als einzige Relation sowohl reflexiv als auch irreflexiv.

Basierend auf einem Artikel in:

Wikipedia.de