Selbstinverse Permutation

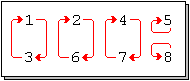
Graph einer selbstinversen Permutation der Zahlen von 1 bis 8. Die Permutation besteht nur aus Zyklen der Länge 1 oder 2.

Eine selbstinverse oder involutorische Permutation ist in der Kombinatorik und der Gruppentheorie eine Permutation, die gleich ihrer Inversen ist. Eine Permutation ist genau dann selbstinvers, wenn ihre Zyklendarstellung ausschließlich aus Zyklen der Länge eins oder zwei besteht. Die Ordnung einer selbstinversen Permutation ist damit maximal zwei. Weiterhin ist die Permutationsmatrix einer selbstinversen Permutation immer symmetrisch. Selbstinverse Permutationen spielen eine wichtige Rolle in der Kryptographie.

Definition

Ist $S_{n}$ die symmetrische Gruppe aller Permutationen der Menge $\{1,\ldots ,n\}$ , dann heißt eine Permutation $\pi \in S_{n}$ selbstinvers oder involutorisch, wenn sie gleich ihrer inversen Permutation $\pi ^{-1}$ ist, wenn also

$\pi = \pi^{-1}$

gilt. Eine dazu äquivalente Forderung ist

$\pi^2 = \operatorname{id}$ ,

wobei $\pi^2 = \pi \circ \pi$ die Hintereinanderausführung von $\pi$ mit sich selbst und $\operatorname {id}$ die identische Permutation sind. Eine selbstinverse Permutation stellt damit eine Involution auf der Menge $\{1,\dotsc ,n\}$ dar. Hat eine selbstinverse Permutation zudem keine Fixpunkte, gilt also $\pi(i) \neq i$ für alle $i=1,\dotsc ,n$ , so spricht man von einer echt selbstinversen Permutation. Man nennt sie auch eine echt involutorische Permutation.

Allgemeiner können auch Permutationen beliebiger endlicher Mengen, beispielsweise Alphabete, betrachtet werden, zur Analyse der mathematischen Eigenschaften kann man sich jedoch auf die ersten natürlichen Zahlen beschränken.

Beispiele

	Selbstinverse Permutationen			Anzahl
1	id			1
2	id	(1 2)		2
3	id	(1 2), (1 3), (2 3)		4
4	id	(1 2), (1 3), (1 4), (2 3), (2 4), (3 4)	(1 2) (3 4), (1 3) (2 4), (1 4) (2 3)	10

Die identische Permutation $\operatorname {id}$ ist trivialerweise selbstinvers, denn es gilt per definitionem

$\operatorname{id}^2 = \operatorname{id} \circ \operatorname{id} = \operatorname{id}$ .

Weiter ist jede Vertauschung (Transposition) $\tau_{ij} = ( i ~ j )$ zweier Zahlen und selbstinvers, denn die zweimalige Anwendung einer solchen Vertauschung tauscht die beiden Zahlen wieder zurück und es gilt damit

$(\tau_{ij})^2 = ( i ~ j )( i ~ j ) = \operatorname{id}$ .

Auch die mehrfache Vertauschung $(i_1 ~ i_2) \ldots (i_{2k-1} ~ i_{2k})$ paarweise verschiedener Zahlen $i_{1},\dotsc ,i_{2k}$ stellt eine selbstinverse Permutation dar, denn aufgrund der Disjunktheit der Zyklen gilt entsprechend

$\left( \tau_{i_1i_2} \circ \ldots \circ \tau_{i_{2k-1}i_{2k}} \right)^2 = (\tau_{i_1i_2})^2 \circ \ldots \circ (\tau_{i_{2k-1}i_{2k}})^2 = \operatorname{id} \circ \ldots \circ \operatorname{id} = \operatorname{id}$ .

Die nebenstehende Tabelle führt alle selbstinversen Permutationen der symmetrischen Gruppen bis zum Grad vier auf. Echt selbstinvers sind davon nur die Permutation $(1~2) \in S_2$ und die drei Permutationen in $S_{4}$ , die je zwei Zahlenpaare vertauschen.

Ein weiteres Beispiel für eine selbstinverse Permutation ist die Spiegelung von n-Tupeln

$\sigma _{n}={\begin{pmatrix}1&2&\dotsb &n\\n&n-1&\dotsb &1\end{pmatrix}}=(1~n)(2~(n-1))(3~(n-2))\cdots$ ,

siehe auch Wort (Theoretische Informatik) §Spiegelung und Palindrom.

Eigenschaften

Nachdem ein Zyklus der Länge erst nach -maliger Hintereinanderausführung zur Identität zurückführen kann und die Zyklendarstellung einer Permutation (bis auf die Reihenfolge der Zyklen und die Anordnung der Zahlen innerhalb der Zyklen) eindeutig ist, ist eine Permutation genau dann selbstinvers, wenn ihre Zyklendarstellung ausschließlich aus Zyklen der Länge eins oder zwei besteht. Eine selbstinverse Permutation $\pi \in S_{n}$ hat also die Zyklendarstellung

$\pi = (i_1 ~ i_2) \ldots (i_{2k-1} ~ i_{2k}) (i_{2k+1}) \ldots (i_n)$ ,

wobei $k \leq n/2$ die Anzahl der Zweier- und n-2k die Anzahl der Einerzyklen bezeichnet. Der Zyklentyp einer selbstinversen Permutation $\pi$ ist demnach von der Form

$\operatorname{typ}(\pi) = 1^{n-2k}2^k$ .

Die selbstinversen Permutationen sind damit genau die Permutationen der Ordnung eins oder zwei, wobei die identische Permutation die einzige Permutation erster Ordnung ist. Die Permutationsmatrix $P_{\pi }$ einer selbstinversen Permutation $\pi$ ist immer symmetrisch, denn es gilt mit der Orthogonalität von Permutationsmatrizen

$P_\pi^T = P_\pi^{-1} = P_{\pi^{-1}} = P_\pi$ .

Umgekehrt entspricht jede symmetrische Permutationsmatrix einer selbstinversen Permutation.

Anzahl

Rekursive Darstellung

${\begin{pmatrix}1&2&3&\dotsb &n\\1&\ast &\ast &\dotsb &\ast \end{pmatrix}}$

${\begin{pmatrix}1&2&3&\dotsb &n\\2&1&\ast &\dotsb &\ast \end{pmatrix}}$

Bei der Herleitung der Rekurrenz sind zwei Fälle zu unterscheiden: Entweder ist $\pi(1) = 1$ oder es sind $\pi(1) = j \neq 1$ und $\pi(j) = 1$ . Im Beispiel ist j=2

Um die Anzahl I_n der selbstinversen Permutationen in der symmetrischen Gruppe $S_{n}$ zu bestimmen, werden die folgenden zwei Fälle unterschieden:

Gilt $\pi(1) = 1$ , dann müssen die übrigen Zahlen eine selbstinverse Permutation der Menge $\{2,\dotsc ,n\}$ bilden, was es $I_{n-1}$ Möglichkeiten gibt.
Ist ansonsten $\pi(1) = j \neq 1$ , dann muss $\pi(j) = 1$ gelten und die übrigen Zahlen müssen eine selbstinverse Permutation der Menge $\{2,\dotsc ,n\}\setminus \{j\}$ bilden, was auf $I_{n-2}$ Arten geschehen kann.

Nachdem es n-1 Möglichkeiten für die Wahl von gibt, folgt daraus für die Anzahl der selbstinversen Permutationen die lineare Rekurrenz

$I_n = I_{n-1} + (n-1) I_{n-2}$

mit den Anfangswerten I_1=1 und I_2=2 . Die Anzahl der selbstinversen Permutationen ergibt für wachsendes die Folge

$1,2,4,10,26,76,232,764,2620,9496,\dotsc$ (Folge A000085 in OEIS)

und ist gleich der Anzahl möglicher Young-Tableaus der Ordnung .

Summendarstellung

Anzahl der Permutationen von Zahlen, die aus disjunkten Transpositionen bestehen
${}_{n}\!\diagdown \!\!{}^{k}$	0	1	2	3	4	5	Summe
1	1						1
2	1	1					2
3	1	3					4
4	1	6	3				10
5	1	10	15				26
6	1	15	45	15			76
7	1	21	105	105			232
8	1	28	210	420	105		764
9	1	36	378	1260	945		2620
10	1	45	630	3150	4725	945	9496

Bezeichnet $I_{n,k}$ die Anzahl der Permutationen in $S_{n}$ , die aus genau disjunkten Transpositionen bestehen, dann gilt für die Anzahl der selbstinversen Permutationen

$I_n = \sum_{k=0}^{\lfloor n/2 \rfloor} I_{n,k}$ ,

wobei $\lfloor ~ \rfloor$ die Gaußklammer darstellt und $I_{n,0}=1$ für alle gilt. Die Zahlen $I_{n,k}$ genügen dabei der linearen Rekurrenz

$I_{n,k} = I_{n-1,k} + (n-2k+1) I_{n-1,k-1}$ (Folge A100861 in OEIS).

Nachdem eine Permutation $\pi \in S_{n}$ , die aus genau disjunkten Transpositionen besteht, den Zyklentyp $\operatorname{typ}(\pi) = 1^{n-2k}2^k$ besitzt, erhält man so die Summendarstellung

$I_n = \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{n!}{(n-2k)! \, k! \, 2^k} = \sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k}(2k-1)!!$ ,

wobei

$(2k-1)!! = 1 \cdot 3 \cdot \ldots \cdot (2k-1) = \frac{(2k)!}{k! \, 2^k}$

die Doppelfakultät ist. Die Zahl (2k-1)!! entspricht gerade der Anzahl $I_{2k,k}$ der echt selbstinversen Permutationen in $S_{2k}$ , also derjenigen Permutationen, die aus genau disjunkten Transpositionen bestehen und somit den Zyklentyp $\operatorname{typ}(\pi) = 2^k$ aufweisen (Folge A001147 in OEIS).

Erzeugende Funktionen

Die exponentiell erzeugende Funktion der Folge I_n der Anzahl der selbstinversen Permutationen ergibt sich als

$f(x) = \sum_{n=0}^\infty I_n \frac{x^n}{n!} = e^{x+x^2/2}$ .

Entsprechend ist die exponentiell erzeugende Funktion der Folge $I_{2k,k}$ der Anzahl der echt selbstinversen Permutationen gleich

$f(x) = \sum_{k=0}^\infty I_{2k,k} \frac{x^{2k}}{(2k)!} = e^{x^2/2}$ .

Anwendungen

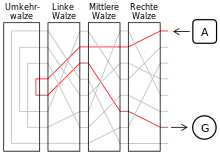
Vertauschung von Buchstaben durch die Verschlüsselungsmaschine Enigma

In der Kryptographie spielen selbstinverse Permutationen eine wichtige Rolle. Wird eine Nachricht mit Hilfe einer selbstinversen Permutation verschlüsselt, dann lässt sich die Nachricht mittels der gleichen Permutation auch wieder entschlüsseln. Ein einfaches Beispiel ist die Caesar-Verschlüsselung ROT13, bei der zur Verschlüsselung jeder Buchstabe durch den um Stellen im Alphabet verschobenen Buchstaben ersetzt wird. Die wiederholte Anwendung ergibt dann eine Verschiebung um Buchstaben und damit wieder die ursprüngliche Nachricht. Eine weitere Möglichkeit einer solchen Verschlüsselung besteht in der Verwendung der bitweisen XOR-Operation, die beispielsweise beim One-Time-Pad verwendet wird. Sehr viel komplexere echt selbstinverse Permutationen führte die deutsche Verschlüsselungsmaschine Enigma durch, die während des Zweiten Weltkriegs zum Einsatz kam.

Die echt selbstinversen Permutationen werden auch zur Berechnung der pfaffschen Determinante einer alternierenden Matrix benötigt. Eine spezielle selbstinverse Permutation wird zur Bitumkehrung bei der effizienten Implementierung der schnellen Fourier-Transformation (FFT) verwendet.

Basierend auf einem Artikel in:

Wikipedia.de