Zykeltyp

Der Zykeltyp, kurz Typ, ist in der Kombinatorik und der Gruppentheorie eine wichtige Eigenschaft von Permutationen. Der Zykeltyp beschreibt die Anzahl und Längen der Zyklen in der Zykeldarstellung einer Permutation. Die Anzahl der möglichen Typen -stelliger Permutationen entspricht gerade der Anzahl der Partitionen der Zahl . Die Anzahl der Permutationen pro Zykeltyp kann aus der Typbeschreibung errechnet werden, wobei die Permutationen mit gleicher Zyklenzahl durch die Stirling-Zahlen erster Art gezählt werden.

Die inverse Permutation weist immer den Typ der Ausgangspermutation auf. Auch das Ergebnis der Komposition zweier Permutationen besitzt unabhängig von der Reihenfolge der Operanden immer den gleichen Zykeltyp. Weiter sind zwei Permutationen genau dann zueinander konjugiert, wenn sie vom gleichen Typ sind. Die Permutationen gleichen Zykeltyps bilden demnach die Konjugationsklassen der symmetrischen Gruppe vom Grad .

Definition

Jede Permutation der symmetrischen Gruppe $S_{n}$ lässt sich eindeutig (bis auf Vertauschung der Faktoren) als Komposition von höchstens paarweise disjunkten Zyklen darstellen. Bezeichnet nun $b_{j}$ für $j=1,\ldots ,n$ die Anzahl der Zyklen der Länge einer Permutation $\pi \in S_{n}$ , dann ist der Zykeltyp dieser Permutation der formale Ausdruck

$\operatorname {typ} (\pi )=1^{b_{1}}2^{b_{2}}\ldots n^{b_{n}}$ ,

wobei die Terme mit $b_{j}=0$ nicht aufgeführt werden müssen. Formal heißt hier, dass das Produkt und die Potenzen nicht tatsächlich ausgerechnet werden. Teilweise wird der Ausdruck auch mit eckigen Klammern versehen. Eine alternative Darstellung des Typs einer Permutation ist das -Tupel

$\operatorname {typ}(\pi )=\left(k_{1},k_{2},\ldots ,k_{s}\right)$ ,

wobei $s \leq n$ und $k_{1}\geq \ldots \geq k_{s}\in \mathbb{N}$ die Längen der Zyklen in der Zykeldarstellung der Permutation in absteigender Reihenfolge sind. Gelegentlich werden die Zyklenlängen auch in aufsteigender Reihenfolge notiert. Beide Darstellungen beinhalten die gleichen Informationen über eine Permutation und können einfach ineinander umgewandelt werden.

Beispiele

Konkrete Beispiele

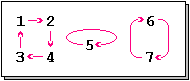
Graph einer Permutation vom Typ $1^{1}2^{1}4^{1}$ oder $(4,2,1)$ .

Die Permutation

$\pi ={\begin{pmatrix}1&2&3&4&5&6&7\\2&4&1&3&5&7&6\end{pmatrix}}=(1243)(5)(67)\in S_{7}$

weist den Zykeltyp

$\operatorname {typ}(\pi )=1^{1}2^{1}3^{0}4^{1}5^{0}6^{0}7^{0}=1^{1}2^{1}4^{1}$ oder $\operatorname {typ}(\pi )=\left(4,2,1\right)$

auf, denn ihre Zykeldarstellung besteht aus je einem Zyklus der Länge eins, zwei und vier. Den gleichen Zykeltyp besitzt etwa auch die Permutation $\pi =(1457)(36)(2)\in S_{7}$ .

Allgemeinere Beispiele>

Die folgenden Arten -stelliger Permutationen $\pi \in S_{n}$ mit $n\geq 2$ besitzen jeweils den zugehörigen Zykeltyp:

identische Permutation:

$\operatorname {typ}(\pi )=1^{n}$ oder $\operatorname {typ}(\pi )=(1,\ldots ,1)$

Transpositionen (Vertauschungen):

$\operatorname {typ}(\pi )=1^{{n-2}}2^{1}$ oder $\operatorname {typ}(\pi )=(2,1,\ldots ,1)$

zyklische Permutationen der Länge $r\geq 2$ :

$\operatorname {typ}(\pi )=1^{{n-r}}r^{1}$ oder $\operatorname {typ}(\pi )=(r,1,\ldots ,1)$

fixpunktfreie Permutationen:

$\operatorname {typ}(\pi )=2^{{b_{2}}}\ldots n^{{b_{n}}}$ oder $\operatorname {typ}(\pi )=\left(k_{1},\ldots ,k_{s}\right)$ mit $k_{j}\geq 2$ für alle

selbstinverse Permutationen:

$\operatorname {typ}(\pi )=1^{{b_{1}}}2^{{b_{2}}}$ oder $\operatorname {typ}(\pi )=\left(k_{1},\ldots ,k_{s}\right)$ mit $k_{j}\leq 2$ für alle

Anzahlen

	Zykeltyp		Zykelstruktur	Anzahl
1	1¹	(1)	( • )	1
2	1²	(1,1)	( • ) ( • )	1
2	2¹	(2)	( • • )	1
3	1³	(1,1,1)	( • ) ( • ) ( • )	1
	1¹ 2¹	(2,1)	( • • ) ( • )	3
	3¹	(3)	( • • • )	2
4	1⁴	(1,1,1,1)	( • ) ( • ) ( • ) ( • )	1
	1² 2¹	(2,1,1)	( • • ) ( • ) ( • )	6
	2²	(2,2)	( • • ) ( • • )	3
	1¹ 3¹	(3,1)	( • • • ) ( • )	8
	4¹	(4)	( • • • • )	6
5	1⁵	(1,1,1,1,1)	( • ) ( • ) ( • ) ( • ) ( • )	1
	1³ 2¹	(2,1,1,1)	( • • ) ( • ) ( • ) ( • )	10
	1¹ 2²	(2,2,1)	( • • ) ( • • ) ( • )	15
	1² 3¹	(3,1,1)	( • • • ) ( • ) ( • )	20
	2¹ 3¹	(3,2)	( • • • ) ( • • )	20
	1¹ 4¹	(4,1)	( • • • • ) ( • )	30
	5¹	(5)	( • • • • • )	24

Zahl der Typen

Für die Anzahl und Längen der Zyklen einer -stelligen Permutation gilt stets

$1\cdot b_{1}+2\cdot b_{2}+\ldots +n\cdot b_{n}=n$ ,

demnach müssen für $n\geq 2$ manche der Zahlen $b_{j}$ gleich null sein. Für die Summe aller Zykellängen gilt entsprechend

$k_{1}+k_{2}+\ldots +k_{s}=n$ .

Daher entspricht die Anzahl der Zykeltypen in $S_{n}$ gerade der Anzahl der Partitionen der Zahl , die durch die Folge

$1,2,3,5,7,11,\ldots$ (Folge A000041 in OEIS)

gegeben ist. In der nebenstehenden Tabelle ist die Anzahl der Zykeltypen in $S_{n}$ die Zahl der Zeilen zu dem gegebenen .

Zahl der Permutationen pro Typ

Die Anzahl der Permutationen $\pi \in S_{n}$ mit $\operatorname {typ} (\pi )=1^{b_{1}}2^{b_{2}}\ldots n^{b_{n}}$ beträgt

${\frac {n!}{b_{1}!\cdot b_{2}!\cdot \ldots \cdot b_{n}!\cdot 1^{{b_{1}}}\cdot 2^{{b_{2}}}\cdot \ldots \cdot n^{{b_{n}}}}}$ (Folge A036039 in OEIS),

denn die Zyklen der Länge können auf $b_{j}!$ verschiedene Weisen angeordnet werden, wobei jeder dieser Zyklen auf verschiedene Weisen geschrieben werden kann. In der nebenstehenden Tabelle finden sich diese Anzahlen in der letzten Spalte. Unter Zuhilfenahme der Tupeldarstellung lässt sich die Anzahl der möglichen Permutationen eines gegebenen Zykeltyps auch durch

${\frac {n!}{b_{1}!\cdot \ldots \cdot b_{n}!\cdot k_{1}\cdot \ldots \cdot k_{s}}}$ ,

angeben. Verwandt dazu sind die Stirling-Zahlen erster Art $s_{n,k}$ , die die Anzahl der -stelligen Permutationen angeben, die genau Zyklen aufweisen. Die Stirling-Zahlen entstehen aus der Summe der Anzahlen der Permutationen mit gleicher Zyklenzahl. Beispielsweise ist die Stirling-Zahl $s_{{5,2}}=30+20=50$ , siehe die zweit- und drittletzte Zeile in der Tabelle.

Zykelklassen

Die Permutationen gleichen Zykeltyps bilden Äquivalenzklassen und man schreibt $\pi \sim \sigma$ , wenn zwei Permutationen $\pi, \sigma \in S_n$ den gleichen Typ besitzen, das heißt

$\pi \sim \sigma \Leftrightarrow \operatorname {typ}(\pi )=\operatorname {typ}(\sigma )$ .

Für die inverse Permutation $\pi ^{-1}$ einer Permutation $\pi$ gilt immer

$\pi ^{{-1}}\sim \pi$ ,

denn durch die Invertierung drehen sich nur die Reihenfolgen der Zahlen innerhalb der einzelnen Zyklen um. Zwar ist die Hintereinanderausführung zweier Permutationen $\pi ,\sigma$ im Allgemeinen nicht kommutativ, aber es gilt stets

$\pi \circ \sigma \sim \sigma \circ \pi$ ,

das Resultat einer Komposition weist also unabhängig von der Reihenfolge der Operanden den gleichen Zykeltyp auf. Auch durch Konjugation mit einer beliebigen Permutation $\sigma$ ändert sich der Typ einer Permutation $\pi$ nicht, das heißt, es gilt

$\sigma \circ \pi \circ \sigma ^{{-1}}\sim \pi$ .

Allgemein sind zwei Permutationen sogar genau dann konjugiert, wenn sie vom gleichen Typ sind. Die -stelligen Permutationen gleichen Zykeltyps bilden daher die Konjugationsklassen der symmetrischen Gruppe $S_{n}$ .

Literatur

Martin Aigner: Diskrete Mathematik. Vieweg, 2006, ISBN 3-8348-9039-1.
Michael Artin: Algebra. Springer, 1998, ISBN 3-7643-5938-2.
Konrad Jacobs, Dieter Jungnickel: Einführung in die Kombinatorik. de Gruyter, 2003, ISBN 3-11-016727-1.
Hans Kurzweil, Bernd Stellmacher: Theorie der endlichen Gruppen: eine Einführung. Springer, 1998, ISBN 3-540-60331-X.
Kristina Reiss, Gernot Stroth: Endliche Strukturen. Springer, 2011, ISBN 3-642-17181-8.

Basierend auf einem Artikel in:

Wikipedia.de