
Zyklische Permutation
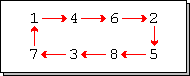
Eine zyklische Permutation, kurz Zyklus oder Zykel (von griechisch κύκλος Kreis), ist in der Kombinatorik und der Gruppentheorie eine Permutation, die bestimmte Elemente einer Menge im Kreis vertauscht und die übrigen festhält. Das erste Element des Zyklus wird dabei auf das zweite abgebildet, das zweite Element auf das dritte, und so weiter bis hin zum letzten Element, das wieder auf das erste abgebildet wird.
Zyklische Permutationen weisen eine Reihe besonderer Eigenschaften auf. So ist die Verkettung zweier zyklischer Permutationen kommutativ, wenn diese disjunkte Träger besitzen. Die inverse Permutation einer zyklischen Permutation ist immer ebenfalls zyklisch. Weiter ergeben beliebige Potenzen einer zyklischen Permutation, deren Länge eine Primzahl ist, wieder zyklische Permutationen. Die zyklischen Permutationen fester Länge bilden zudem Konjugationsklassen der symmetrischen Gruppe aller Permutationen.
Jede zyklische Permutation kann in einzelne Transpositionen zerlegt werden und weist daher genau dann ein gerades Vorzeichen auf, wenn ihre Länge ungerade ist. Jede Permutation kann wiederum als Verkettung paarweise disjunkter Zyklen geschrieben werden, was in der Zykelschreibweise von Permutationen genutzt wird. Die Ordnung einer Permutation entspricht dann dem kleinsten gemeinsamen Vielfachen der Längen dieser Zyklen. Zyklische Permutationen mit großer Zykellänge spielen eine wichtige Rolle bei der Konstruktion von Pseudozufallszahlengeneratoren.
Definition
Ist
die symmetrische
Gruppe aller Permutationen
der Menge
,
dann heißt eine Permutation
zyklisch mit der Länge
oder
-Zyklus,
wenn sie eine Liste von
paarweise verschiedenen Zahlen
im Kreis vertauscht, das heißt
,
und alle anderen Zahlen festhält. Es muss also gelten
und
sowie
für
.
Die Menge
heißt der Träger oder die Bahn von
.
Allgemeiner können auch Permutationen beliebiger endlicher
Mengen, beispielsweise Alphabete,
betrachtet werden, zur Analyse der mathematischen Eigenschaften kann man sich
jedoch auf die ersten
natürlichen Zahlen beschränken.
Notation
Neben der obigen Funktionsnotation, bei der die Abbildung
vollständig angegeben wird, kann eine zyklische Permutation auch dadurch notiert
werden, dass lediglich die Zahlen, die zyklisch vertauscht werden, als Indizes mittels
angegeben werden. Häufig wird eine zyklische Permutation auch in Zykelschreibweise notiert, indem diese Zahlen ohne Trennzeichen in Klammern gesetzt werden:
In beiden Schreibweisen wird davon ausgegangen, dass die Gesamtzahl
der Zahlen bekannt ist. Die Index- und Zykelschreibweisen sind allerdings nicht
eindeutig, denn die Startzahl kann innerhalb des Zyklus beliebig gewählt werden.
Jeder
-Zyklus
kann so auf
verschiedene Weisen
oder
beschrieben werden. Oft gesetzte Konvention ist aber, für
die kleinste oder die größte Zahl des Zyklus zu wählen.
Beispiele
| Länge | Zyklische Permutationen | Anzahl |
|---|---|---|
| 1 | id | 1 |
| 2 | (1 2), (1 3), (1 4), (2 3), (2 4), (3 4) |
6 |
| 3 | (1 2 3), (1 2 4), (1 3 2), (1 3 4), (1 4 2), (1 4 3), (2 3 4), (2 4 3) |
8 |
| 4 | (1 2 3 4), (1 2 4 3), (1 3 2 4), (1 3 4 2), (1 4 2 3), (1 4 3 2) |
6 |
Eine einfache zyklische Permutation der Länge drei ist
.
Hierbei wird die Zahl
auf die Zahl
,
die Zahl
auf die Zahl
und die Zahl
wieder auf die Zahl
abgebildet. Die Permutation
ist eine zyklische Permutation der Länge zwei, bei der die Zahlen
und
vertauscht werden und die Zahlen
und
festgehalten werden. Jede zyklische Permutation der Länge eins
entspricht gerade der identischen
Permutation ,
die alle Zahlen unverändert lässt. In der symmetrischen Gruppe
finden sich die in der nebenstehenden Tabelle aufgeführten zyklischen
Permutationen. Von den
Permutationen in
sind demnach nur drei Permutationen nichtzyklisch, nämlich diejenigen, die
jeweils zwei Paare von Zahlen vertauschen.
Spezialfälle
Bei zyklischen Permutationen werden folgende Spezialfälle betrachtet:
- Vertauschung oder Transposition: Eine zyklische Permutation, die genau zwei Elemente miteinander vertauscht, also
-
für
.
- Nachbarvertauschung oder Nachbartransposition: Eine zyklische Permutation, die zwei aufeinander folgende Elemente miteinander vertauscht, also
-
für
.
- Zyklischer Rechtsshift: Eine zyklische Permutation, die alle Elemente der Reihe nach aufsteigend im Kreis vertauscht, also
-
.
- Zyklischer Linksshift: Eine zyklische Permutation, die alle Elemente der Reihe nach absteigend im Kreis vertauscht, also
-
.
Eigenschaften
Anzahl
| 1 | 2 | 3 | 4 | 5 | 6 | Summe | |
| 1 | 1 | 1 | |||||
| 2 | 1 | 1 | 2 | ||||
| 3 | 1 | 3 | 2 | 6 | |||
| 4 | 1 | 6 | 8 | 6 | 21 | ||
| 5 | 1 | 10 | 20 | 30 | 24 | 85 | |
| 6 | 1 | 15 | 40 | 90 | 144 | 120 | 410 |
In der Menge der
verschiedenen Permutationen der Zahlen
gibt es genau
viele
-Zyklen.
Jeder Permutation in Tupelschreibweise
entspricht nämlich ein
-Zyklus
,
der wiederum auf
verschiedene Weisen geschrieben werden kann. Bezeichnet nun allgemein
die Menge der
-Zyklen
in
,
dann gilt für
denn es gibt
Möglichkeiten,
von
Zahlen auszuwählen. Für die Gesamtmenge
aller zyklischen Permutationen in
inklusive der identischen Permutation gilt damit:
Kommutativität
Im Allgemeinen ist die Hintereinanderausführung
zweier zyklischer Permutationen nicht kommutativ.
Besitzen allerdings zwei zyklische Permutationen
und
disjunkte
Träger, gilt also
,
dann lässt sich ihre Reihenfolge bei der Hintereinanderausführung vertauschen, das heißt, es gilt
.
Zyklische Permutationen mit disjunkten Trägern werden auch disjunkte Zyklen genannt.
Abgeschlossenheit und Inverse
Die Hintereinanderausführung zweier zyklischer Permutationen ist nicht notwendigerweise wieder zyklisch, wie das Beispiel
zeigt. Daher bildet die Menge der zyklischen Permutationen
für
keine Untergruppe der
symmetrischen Gruppe
.
Allerdings ist die inverse
Permutation einer zyklischen Permutation
stets ebenfalls eine zyklische Permutation, nämlich diejenige, die die Zahlen
in umgekehrter Reihenfolge zyklisch vertauscht, also
.
Die inverse Permutation einer Transposition ist damit wieder die gleiche Transposition.
Potenzen
Wird eine zyklische Permutation zweimal hintereinander angewandt, so
verschieben sich alle Indizes zyklisch um ,
das heißt
wird auf
abgebildet,
auf
und so weiter bis hin zu
auf
und
auf
.
Allgemein verschieben sich durch die
-malige
Anwendung einer zyklischen Permutation alle Indizes zyklisch um
.
Die
-te
Potenz einer zyklischen Permutation der Länge
ist genau dann selbst wieder zyklisch, wenn
und
teilerfremd
sind. Speziell ergibt die
-malige
Anwendung einer zyklischen Permutation
die identische Permutation, also
,
und die -malige
Anwendung ergibt wieder die Ausgangspermutation, also
.
Daher bildet die Menge
mit der Hintereinanderausführung eine Untergruppe der symmetrischen Gruppe
,
wobei
das inverse
Element zu
ist. Diese Untergruppe ist isomorph
zur zyklischen
Gruppe
und besteht genau dann ausschließlich aus zyklischen Permutationen, wenn
eine Primzahl ist.
Konjugation
Für eine zyklische Permutation
berechnet sich die Konjugation
mit einer beliebigen Permutation
zu
,
sie ergibt also wiederum einen -Zyklus.
Die Menge
bildet dabei für jedes
eine Konjugationsklasse
der Gruppe
.
Allgemein sind zwei Permutationen
genau dann zueinander konjugiert, wenn ihr Zykeltyp
übereinstimmt.
Zerlegungen
Zerlegung von Zyklen in Teilzyklen
Jede zyklische Permutation der Länge
lässt sich an einer beliebigen Stelle
mittels
in zwei Teilzyklen zerlegen. Wendet man diese Zerlegung wiederholt mit
an, ergibt sich, dass jede zyklische Permutation der Länge
mittels
.
als Verkettung von
Transpositionen geschrieben werden kann. Für das Vorzeichen
einer zyklischen Permutation der Länge
gilt damit
,
da Transpositionen immer ein ungerades Vorzeichen haben. Eine zyklische Permutation ist also genau dann gerade, wenn ihre Länge ungerade ist.
Beispiel
Die zyklische Permutation
der Länge vier lässt sich durch
in drei Transpositionen zerlegen und ist demnach ungerade.
Zerlegung von Permutationen in Zyklen
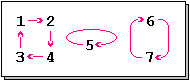
Jede Permutation
lässt sich eindeutig (bis auf Vertauschung der Faktoren) als Verkettung von
paarweise disjunkten Zyklen darstellen. Das heißt, es gilt
mit paarweise disjunkten Trägern
für
,
wobei
ist. Die Stirling-Zahlen
erster Art
geben dabei an, wie viele Permutationen in
als Verkettung von genau
zyklischen Permutationen geschrieben werden können. Die Ordnung einer
Permutation entspricht der Ordnung der zugehörigen
zyklischen Gruppe und ist damit das kleinste
gemeinsame Vielfache der Längen
dieser Zyklen. Weiter ergibt sich das Vorzeichen einer Permutation aus der Zahl
der Zyklen gerader Länge.
Beispiel
Die Permutation
zerfällt in die drei disjunkten Zyklen
und hat damit die Ordnung .
Da nur einer der drei Zyklen eine gerade Länge hat, ist die Permutation
ungerade.
Anwendungen
Zyklische Permutationen mit großer Zykellänge spielen eine wichtige Rolle bei der Konstruktion von Pseudozufallszahlengeneratoren. Die maximale Periode eines solchen Zufallszahlengenerators entspricht der Anzahl der möglichen Zustände des Generators. Bei einfachen rekursiven Generatoren der Form
mit
ist die Zahl der möglichen Zustände gerade
.
Die Periode eines solchen Generators ist genau dann maximal, wenn die Funktion
eine zyklische Permutation der Länge
der Menge
darstellt. Im Fall von linearen
Kongruenzgeneratoren der Art
gibt der Satz
von Knuth hinreichende und notwendige Bedingungen an die Parameter
und
für die Maximalität der Periodenlänge.
Siehe auch


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 16.11. 2021