Website durchsuchen

Zusammenhang (Graphentheorie)

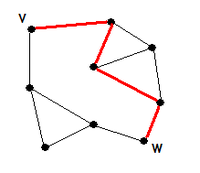
Ein zusammenhängender Graph: Je zwei Knoten lassen sich durch eine Kantenfolge verbinden. Exemplarisch ist eine Kantenfolge zwischen den Knoten v und w rot hervorgehoben.

Der Zusammenhang ist ein mathematischer Begriff aus der Graphentheorie. Ein Graph heißt zusammenhängend, wenn die Knoten paarweise durch eine Kantenfolge des Graphen verbunden sind.

Definition

Ungerichtete Graphen

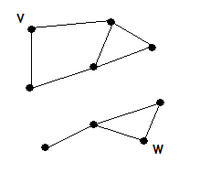
Dieser unzusammenhängende Graph hat zwei Komponenten, die Knoten v und w können nicht verbunden werden.

Ein ungerichteter Graph G=(V,E) heißt zusammenhängend, falls es zu je zwei beliebigen Knoten v und w aus V einen ungerichteten Weg in G mit v als Startknoten und w als Endknoten gibt.

Einen maximalen zusammenhängenden Teilgraphen eines beliebigen Graphen nennt man eine Komponente oder Zusammenhangskomponente. Ein nicht zusammenhängender Graph zerfällt in seine Zusammenhangskomponenten.

Gerichtete Graphen

Ein gerichteter Graph G=(V,E) heißt (stark) zusammenhängend von einem Knoten v aus, falls es zu jedem Knoten w aus V einen gerichteten Weg in G von v nach w gibt. G heißt stark zusammenhängend, falls G von jedem Knoten aus stark zusammenhängend ist. Anders formuliert heißt G stark zusammenhängend, falls es zwischen zwei beliebigen Knoten u und v aus G sowohl einen gerichteten Weg von u nach v wie auch einen gerichteten Weg von v nach u in G gibt.

Ein gerichteter Graph heißt (schwach) zusammenhängend, falls der zugehörige ungerichtete Graph (also der Graph, der entsteht, wenn man jede gerichtete Kante durch eine ungerichtete Kante ersetzt) zusammenhängend ist.

Ein induzierter Teilgraph G[U] für eine Teilmenge U\subset V heißt starke Zusammenhangskomponente von G, falls G[U] stark zusammenhängend ist und nicht zu einem größeren stark zusammenhängenden Teilgraphen von G erweitert werden kann.

Wichtige Aussagen und Sätze

Relativ leicht zeigt man folgende Aussagen:

  1. Jeder zusammenhängende ungerichtete Graph mit n Knoten enthält mindestens n-1 Kanten.
  2. Jeder stark zusammenhängende gerichtete Graph mit n Knoten enthält mindestens n Kanten.
  3. Ein ungerichteter Graph ist genau dann zusammenhängend, wenn er einen Spannbaum enthält.
  4. Ein gerichteter Graph ist genau dann stark zusammenhängend, wenn seine Adjazenzmatrix irreduzibel ist. Damit ist auch ein ungerichteter Graph genau dann zusammenhängend, wenn seine Adjazenzmatrix irreduzibel ist.

Wichtige Algorithmen

Mittels Tiefensuche lässt sich leicht ein linearer Algorithmus implementieren, der die Zusammenhangskomponenten eines Graphen berechnet und so einen einfachen Test impliziert, ob der Graph zusammenhängend ist. Der Test, ob ein gerichteter Graph von einem Knoten v aus zusammenhängend ist, funktioniert analog. Von Tarjan (1972) stammt ein linearer Algorithmus zur Bestimmung starker Zusammenhangskomponenten, der ebenfalls auf Tiefensuche basiert und in gerichteten Graphen die starken Zusammenhangskomponenten und leicht modifiziert in ungerichteten Graphen die Blöcke und Artikulationen berechnet.

Verallgemeinerungen

Eine wesentliche Verallgemeinerung des Begriffs stellt der Begriff des k-fachen Knotenzusammenhangs, der Kantenzusammenhang und der Bogenzusammenhang dar.

Trenner
Basierend auf einem Artikel in: Wikipedia.de
Seitenende
Seite zurück
©  biancahoegel.de
Datum der letzten Änderung:  Jena, den: 20.10. 2019