
k-Zusammenhang
Der k-Zusammenhang eines Graphen ist ein wichtiger Begriff in der Graphentheorie und eine Verallgemeinerung des Zusammenhangs. Anschaulich ist der k-Zusammenhang ein Maß dafür, wie schwierig es ist, einen Graphen durch Löschen von Knoten in zwei Komponenten zu zerlegen. Ist der k-Zusammenhang groß, so müssen viele Knoten gelöscht werden.
Definition
Ungerichtete Graphen
Ein ungerichteter Graph
(welcher auch ein Multigraph
sein kann) heißt k-fach knotenzusammenhängend (oder auch einfach
k-fach zusammenhängend oder k-zusammenhängend), wenn es keinen Trenner
in
mit einer maximal
-elementigen
Knotenmenge
und leerer Kantenmenge
gibt. Äquivalent dazu ist, dass für alle Knotenmengen
mit Mächtigkeit
der von
induzierte
Teilgraph zusammenhängend ist.
Ist
eine Teilmenge der Knotenmenge
mit der Eigenschaft, dass der von
induzierte
Teilgraph
-zusammenhängend
ist und
für jede Knotenmenge
nicht
-zusammenhängend
ist, so nennt man
eine k-Zusammenhangskomponente von
.
Eine 2-Zusammenhangskomponente nennt man auch einen Block.
Als Knotenzusammenhangszahl
(oft kurz Zusammenhangszahl oder Zusammenhang genannt) eines Graphen
bezeichnet man das größte
,
sodass
-zusammenhängend
ist. Eine dazu äquivalente Definition ist, dass die Knotenzusammenhangszahl die
kleinste Mächtigkeit eines Trenners von
mit leerer Kantenmenge ist. Graphen, die k-zusammenhängend sind, haben
Zusammenhangszahlen
,
die größer gleich
sind:
.
Gerichtete Graphen
Ein gerichteter
Graph
(welcher auch Mehrfachkanten enthalten kann) heißt k-fach stark
zusammenhängend, wenn für jede Knotenmenge
der Mächtigkeit
der von
induzierte
Teilgraph
stark
zusammenhängend ist.
Das größte ,
so dass
-fach
stark zusammenhängend ist, wird starke Zusammenhangszahl genannt und mit
bezeichnet.
Beispiel
K-facher Zusammenhang
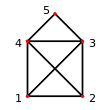
Betrachte als Beispiel das rechts dargestellte Haus vom Nikolaus. Es
ist 2-zusammenhängend, da keine Trenner existieren, die nur aus einem Knoten
bestehen. Äquivalent dazu ist, dass keine Artikulation
existiert. Betrachtet man aber nun z.B. die Knoten 3 und 4, so trennen
diese das Haus in die Knotenmengen 5 sowie 1 und 2, da jeder Weg von 5 nach 1
oder 2 durch einen der Knoten 3 oder 4 gehen muss. Das Haus ist also einfach und
zweifach knotenzusammenhängend und seine Knotenzusammenhangszahl ist .
K-fach starker Zusammenhang
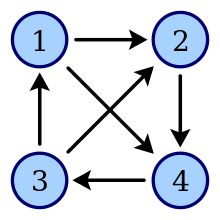
Betrachte als Beispielgraph den rechts dargestellten Turniergraph. Der Graph
ist stark zusammenhängend, also auf jeden Fall einfach stark zusammenhängend.
Beginnt man mit dem Löschen von einelementigen Knotenmengen, so wird der starke
Zusammenhang jedoch bald zerstört. Entfernt man z.B. den Knoten 3, so ist
der Knoten 2 von Knoten 4 aus nicht mehr erreichbar. Somit ist der Digraph
einfach stark zusammenhängend und .
Eigenschaften
- Jeder
-zusammenhängende Graph ist auch
-zusammenhängend (da es keine
-elementige Knotenmenge gibt, die
trennt, gibt es natürlich auch keine
-elementige).
- Ein einfacher Graph ist genau dann 2-zusammenhängend, wenn er keine Artikulation besitzt.
- Eine 1-Zusammenhangskomponente ist genau die klassische Zusammenhangskomponente.
- Ist
, so gilt
, wobei
die Kantenzusammenhangszahl und
der Minimalgrad des Graphen
ist. Hoher Zusammenhang setzt also hohen Minimalgrad voraus. Der Umkehrschluss gilt jedoch nicht.
ist genau dann
-zusammenhängend, wenn
zwischen je zwei Knoten
disjunkte Wege enthält. Diese Aussage ist auch als die globale Version des Satzes von Menger bekannt.
Algorithmen
Bestimmung der Knotenzusammenhangszahl
Zur Berechnung der Knotenzusammenhangszahl gibt es polynomielle
Algorithmen. Dazu kann man beispielsweise Flussalgorithmen
verwenden. Hierfür berechnet man für alle Knotenpaare
einen maximalen
-
-Fluss.
Der kleinste Wert, den der Fluss annimmt, ist dann nach dem Satz von Menger die
Knotenzusammenhangszahl. Ist also
der benötigte Aufwand, einen
-
-Fluss
in einem Graphen mit n Knoten und m Kanten zu bestimmen, so liefert dieser naive
Ansatz immerhin einen Aufwand von
.
Allerdings gibt es auch effizientere Algorithmen.
Ein sehr guter, aber komplizierter Algorithmus zur Berechnung des Kantenzusammenhangs eines gerichteten (und damit auch ungerichteten) Graphen mit rationalen Gewichten wurde von H. Gabow entwickelt (basierend auf der Matroid-Theorie, also einer Menge von Teilbäumen).
Ein leichter und auch für reelle Gewichte geeigneter Algorithmus existiert, entdeckt von Stoer/Wagner und zeitgleich Nagamotchi/Ibaraki. Dieser funktioniert mittels Knotenkontraktion und nur für ungerichtete Graphen.
Ein auf Flussalgorithmen basierender Algorithmus für gerichtete Graphen wurde von Hao/Orlin vorgestellt.
Test auf k-Zusammenhang
Ist man nicht an der Knotenzusammenhangszahl interessiert, sondern will man
nur wissen, ob ein Graph k-zusammenhängend ist für vorgegebenes k, so gibt es
schnelle Algorithmen. So kann der 2-Zusammenhang in linearer Zeit bestimmt
werden. Für ungerichtete Graphen gibt es lineare Algorithmen, die einen
3-Zusammenhang überprüfen. Für 4-Zusammenhang in ungerichteten Graphen
existieren Algorithmen mit Aufwand
Verwandte Begriffsbildungen
Der Kantenzusammenhang ist ein zum k-Zusammenhang ähnlicher Begriff, bloß dass nur Trenner mit leerer Knotenmenge und einer beliebigen Kantenmenge betrachtet werden. Der Kantenzusammenhang gibt also ein Maß dafür an, wie viele Kanten aus einem Graphen entfernt werden müssen, so dass dieser in verschiedene Komponenten zerfällt. Einen zum Kantenzusammenhang analogen Begriff für gerichtete Graphen bildet der Bogenzusammenhang, welcher anstelle von ungerichteten Kanten gerichtete Kanten betrachtet.
Anzahl einfacher nicht-isomorpher unbenannter Graphen
Anzahl der verschiedenen nicht-isomorphen
einfachen unbenannten
-zusammenhängenden
Graphen mit
Knoten für
von 1 bis 9, inklusive der Referenz OEIS
(einfache Graphen umfassen sowohl zusammenhängende, wie auch nicht
zusammenhängende):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | OEIS | |
|---|---|---|---|---|---|---|---|---|---|---|
| einfach | 1 | 2 | 4 | 11 | 34 | 156 | 1044 | 12346 | 274668 | A000088 |
| 1 | 1 | 1 | 2 | 6 | 21 | 112 | 853 | 11117 | 261080 | A001349 |
| 2 | 0 | 1 | 1 | 3 | 10 | 56 | 468 | 7123 | 194066 | A002218 |
| 3 | 0 | 0 | 1 | 1 | 3 | 17 | 136 | 2388 | 80890 | A006290 |
| 4 | 0 | 0 | 0 | 1 | 1 | 4 | 25 | 384 | 14480 | A086216 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 4 | 39 | 1051 | A086217 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 5 | 59 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 5 |
Anzahl der verschiedenen nicht-isomorphen einfachen unbenannten Graphen mit
Knoten und der Knotenzusammenhangszahl
:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | OEIS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 5 | 13 | 44 | 191 | 1229 | 13588 | |
| 1 | 1 | 0 | 1 | 3 | 11 | 56 | 385 | 3994 | 67014 | A052442 |
| 2 | 0 | 1 | 0 | 2 | 7 | 39 | 332 | 4735 | 113176 | A052443 |
| 3 | 0 | 0 | 1 | 0 | 2 | 13 | 111 | 2004 | 66410 | A052444 |
| 4 | 0 | 0 | 0 | 1 | 0 | 3 | 21 | 345 | 13429 | A052445 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 34 | 992 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 4 | 54 |
Literatur
- Reinhard Diestel: Graphentheorie. Springer, Berlin 2010, ISBN 978-3-642-14911-5.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.12. 2025