Teilgraph
Der Begriff Teilgraph beschreibt in der Graphentheorie eine
Beziehung zwischen zwei Graphen.
Ein anderes Wort für Teilgraph ist Untergraph. Ein Graph
ist Teilgraph des Graphen
,
wenn alle Knoten und Kanten von
auch in
enthalten sind. Anders gesagt: Ein Teilgraph
entsteht aus einem Graphen
,
indem einige Knoten und Kanten aus
entfernt werden. Dabei müssen beim Entfernen eines Knotens auch alle inzidenten
Kanten mit entfernt werden.
Definitionen
Ein Graph
heißt Teilgraph oder Untergraph oder Subgraph von
,
wenn seine Knotenmenge
Teilmenge von
und seine Kantenmenge
Teilmenge von
ist, also
und
gilt.
Umgekehrt heißt
dann Supergraph oder Obergraph von
.
Diese Bezeichnungen sind nicht einheitlich. Im unten angegebenen Lehrbuch von Klaus Wagner
wird in dieser Allgemeinheit nur der Begriff Teilgraph verwendet und ein
Untergraph als Teilgraph definiert, der zusätzlich die Eigenschaft hat,
dass jede Kante aus ,
die zwei Knoten aus
verbindet, auch eine Kante in
ist. Im Lehrbuch von Claude Berge
bedeutet Teilgraph zusätzlich, dass
ist, und Untergraph, dass
und jede Kante aus
,
die zwei Knoten aus
verbindet, auch eine Kante in
ist, der allgemeine Fall heißt dann dort Teil-Untergraph. Es empfiehlt
sich daher, bei jedem Autor, die verwendete Definition zu prüfen.
Bei einem knotengewichteten
bzw. kantengewichteten
Graphen
wird von einem Teilgraphen
zudem verlangt, dass die Gewichtsfunktion
von
kompatibel zu der Gewichtsfunktion
von
sein muss, d.h. für jeden Knoten
gilt
bzw. für jede Kante
gilt
.
Gilt für einen Teilgraphen
zusätzlich, dass
alle Kanten zwischen den Knoten in
enthält, die auch in
vorhanden sind, so bezeichnet man
als den durch
induzierten Teilgraphen von
und notiert diesen auch mit
.
Ein induzierter Teilgraph ist also immer eindeutig durch den Obergraphen und
die gewählte Knotenmenge bestimmt. Für eine Knotenmenge
bezeichnet man mit
den induzierten Teilgraphen, der aus
durch Weglassen der Knoten aus
und aller mit diesen Knoten inzidenten Kanten entsteht, also
.
Ein Teilgraph
von
,
der alle Knoten seines Obergraphen enthält, wird aufspannender Teilgraph
oder Faktor genannt.
Beispiele
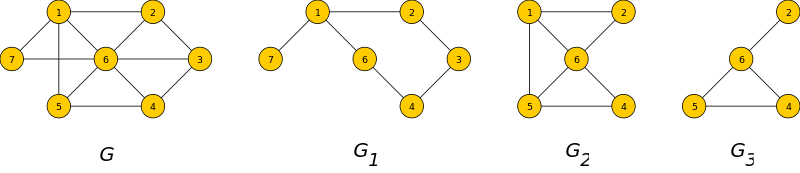
In der folgenden Abbildung sind die Graphen ,
und
Teilgraphen von
,
aber nur
und
sind induzierte Teilgraphen.
entsteht dabei aus
durch Weglassen der Knoten
und ihrer inzidenten Kanten, also ist
.
Gleichzeitig ist
auch ein induzierter Teilgraph von
.
Siehe auch
Literatur
- Klaus Wagner: Graphentheorie, BI-Hochschultaschenbücher (1969), Band 248
- Claude Berge: Programme, Spiele, Transportnetze, Teubner-Verlag 1969


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.03. 2019