Minor (Graphentheorie)
In der Graphentheorie sind Minoren gewisse Graphen, die sich durch Kantenkontraktion und durch Weglassen von Kanten oder Knoten aus einem anderen Graphen gewinnen lassen. Die Minorenrelation ist neben der Teilgraphenrelation und der Unterteilungsrelation eine der wichtigsten Relationen der Graphentheorie und erlaubt viele tiefgehende Sätze wie z.B. den Satz von Kuratowski oder den Satz von Robertson-Seymour.
Definition
Alle genannten Graphen seien stets als einfach angenommen.
Minor
Ersetzt man die Knoten
eines Graphen
durch disjunkte zusammenhängende
Graphen
sowie Kanten
durch
-
-Kanten,
so erhält man einen neuen Graphen, der
genannt wird (
für inflated, auf Deutsch aufgeblasen. Diese Benennung leitet sich
daraus her, dass durch die Ersetzung der Knoten durch Graphen der ursprüngliche
Graph „größer“ wird). Enthält nun ein Graph
ein
,
so nennt man
einen Minor von
.
Topologischer Minor
Ist
ein Graph, so heißt ein Graph
Unterteilungsgraph
von
,
falls er durch Unterteilung von Kanten aus
hervorgegangen ist. Die Knoten von
,
die auch in
enthalten sind, werden dann Verzweigungsknoten genannt, alle anderen
Knoten heißen Unterteilungsknoten. Verzweigungsknoten erben ihren Grad
aus
,
Unterteilungsknoten sind alle von Grad zwei. Enthält ein Graph
einen Unterteilungsgraphen
eines Graphen
,
so nennt man
einen topologischen Minor von
.
Äquivalente Definitionen
Folgende Definitionen finden sich auch gelegentlich in der Literatur:
- Minor
Ein Graph
heißt ein Minor von
,
wenn
einen Teilgraph enthält, aus dem
durch Kantenkontraktion
hervorgeht.
- Topologischer Minor
Ein Graph
heißt topologischer Minor von
,
wenn
einen Unterteilungsgraphen von
enthält.
Beispiel
Minor
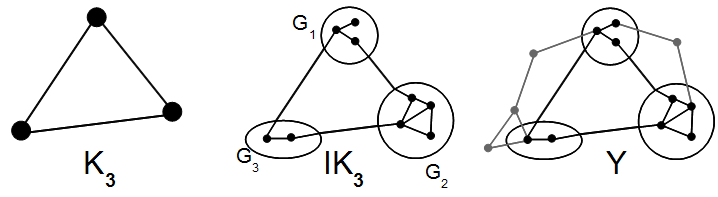
Links außen ist der vollständige
Graph mit drei Knoten
abgebildet. Dieser entsteht durch Kantenkontraktion aus dem Graph
,
der wiederum in
enthalten ist.
ist also ein Minor von
.
Topologischer Minor
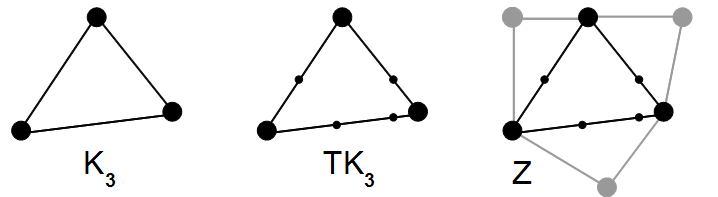
Links außen ist der vollständige Graph mit drei Knoten, mittig ein
Unterteilungsgraph abgebildet. Der Unterteilungsgraph ist aber im Graphen
enthalten,
ist also topologischer Minor von
.
Eigenschaften
- Die Minorenrelation
definiert eine Ordnungsrelation auf den endlichen Graphen, das heißt, sie ist reflexiv, transitiv und antisymmetrisch (dasselbe gilt auch für die topologische Minorenrelation).
- Jeder Teilgraph eines Graphen ist auch ein Minor dieses Graphen.
- Jedes
ist auch ein
. Damit ist jeder topologische Minor auch ein gewöhnlicher Minor.
- Nicht jeder Minor ist auch ein topologischer Minor. Ein Beispiel dafür ist
der Petersen-Graph
und dessen Minor
.
- Die Minorenrelation definiert eine Wohlquasiordnung auf den endlichen Graphen. Dieser Satz ist auch als Minorentheorem bekannt.
- Die Determinante der Adjazenzmatrix eines Minors ist gerade der dem Untergraphen entsprechende Minor im Sinne der Matrizenrechnung der Adjazenzmatrix des ursprünglichen Graphen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.03. 2019