Vollständiger Graph
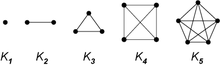
Ein vollständiger Graph ist ein Begriff aus der Graphentheorie und
bezeichnet einen einfachen
Graphen, in dem jeder Knoten
mit jedem anderen Knoten durch eine Kante
verbunden ist. Der vollständige Graph mit
Knoten ist (bis auf Isomorphie)
eindeutig bestimmt und wird mit
bezeichnet.
Ist
die Knotenmenge des vollständigen Graphen
,
so ist die Kantenmenge
genau die Menge von Kanten zwischen paarweise verschiedenen Knoten
.
Ein vollständiger Graph ist gleichzeitig seine maximale Clique.
Eigenschaften
Die vollständigen Graphen
bis
sind planar.
Alle anderen vollständigen Graphen sind nach dem Satz von Kuratowski
nicht planar, da sie
als Teilgraph enthalten.
Die Anzahl der Kanten des vollständigen Graphen
entspricht der Dreieckszahl
.
Der vollständige Graph
ist ein
-regulärer
Graph: jeder Knoten hat
Nachbarn.
Aufgrund dessen hat jede Knotenfärbung
des Graphen
Farben. Des Weiteren folgt daraus, dass die vollständigen Graphen für ungerade
eulersch
sind und für gerade
nicht.
Vollständige Graphen sind für
hamiltonsche
Graphen. Der vollständige Graph
enthält dabei
verschiedene Hamiltonkreise.
Verallgemeinerung
Die Idee des vollständigen Graphen lässt sich auf -partite
Graphen übertragen. Diese sind vollständig, falls jeder Knoten einer
Partition mit allen Knoten aller anderen Partitionen verbunden ist. Den
vollständigen multipartiten Graphen mit
Partitionsmengen, welche
Knoten enthalten, bezeichnet man mit
.
Versieht man einen vollständigen Graphen mit einer Orientierung, so erhält man einen Turniergraphen.
Software
Mit Hilfe der freien Python-Bibliothek NetworkX lassen sich vollständige Graphen erzeugen. Beispiel:
import networkx as nx
import matplotlib.pyplot as plt
G = nx.complete_graph(15)
nx.draw_circular(G, with_labels=True, font_weight='bold')
plt.show()


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.06. 2021