
Weg (Graphentheorie)
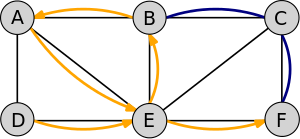
In der Graphentheorie bezeichnet Weg, Pfad, Kantenzug oder Kantenfolge eine Folge von Knoten, in welcher jeweils zwei aufeinander folgende Knoten durch eine Kante verbunden sind.
Definitionen
Weg
Ein nicht-leerer Graph
,
mit der Knotenmenge
und der Kantenmenge
,
heißt Weg, wenn die Knoten
paarweise verschieden sind. Oft wird ein Weg der Einfachheit halber durch die
Folge seiner Knoten
angegeben. Hierbei gilt es, zu beachten, dass auch die gespiegelte Folge
diesen Weg benennt. Nach dieser Definition besitzen Wege keine ausgezeichnete
Richtung. Die Knoten
und
nennt man die Endknoten des Weges. Knoten, die keine Endknoten sind,
nennt man auch innere Knoten.
Im sprachlichen Gebrauch sagt man oft, ein Graph enthalte einen Weg. Das soll
bedeuten, dass dieser Weg ein Teilgraph
des Graphen ist. Je nach Kontext kann man den Begriff Weg anpassen. Bei gerichteten Graphen
müssen zum Beispiel alle aufeinander folgenden Knoten
und
durch eine gerichtete Kante
verbunden sein, sodass der Weg auch eine Richtung angibt.
Der Begriff des Weges wird in der Literatur nicht einheitlich verwendet. Die angegebene Definition folgt im Wesentlichen den Büchern von Reinhard Diestel und László Lovász. In unmissverständlichen Zusammenhängen - und vor Allem im Falle der schlichten Graphen - wird in der graphentheoretischen Fachliteratur ein Weg auch direkt über die Folge der benachbarten Knoten angegeben, so etwa bei Martin Aigner und Dénes Kőnig. Gelegentlich wird auch der Begriff Pfad für einen Weg verwendet (Steger), wohl deshalb, weil in der englischsprachigen Literatur Weg als path, teilweise aber auch als simple path bezeichnet wird.
Ein Weg, bei dem der Start- mit dem Endknoten identisch ist, nennt man Zyklus und wenn dies der einzige wiederholte Knoten in der Knotenfolge ist, heißt dieser Kreis.
Kantenzug, Kantenfolge, Bahn
In einem (gerichteten) Graphen nennt man eine Folge ,
in der sich Knoten und Kanten des Graphen abwechseln und für die gilt, dass für
die Kante
die Form
hat, einen Kantenzug des Graphen. Des Weiteren können sich Kanten und
Knoten innerhalb eines Kantenzuges wiederholen. Ein Kantenzug von
nach
impliziert die Existenz eines Pfades mit den Endknoten
und
.
Kantenzüge bei denen der erste und der letzte Knoten übereinstimmen heißen
geschlossen.
Ein besonderes Interesse gilt solchen Kantenzügen, die geschlossenen sind und in denen jede Kante des Graphen genau einmal auftritt. Einen solchen Kantenzug nennt man nach Leonhard Euler eulersch oder einfach einen Eulerzug oder auch eine eulersche Linie. Die Existenz solcher wurde von Euler im Zusammenhang mit der Lösung des Königsberger Brückenproblems (1736) untersucht, welches als eines der Initialprobleme der Graphentheorie gilt.
Auch der Begriff des Kantenzuges wird in der Fachliteratur nicht einheitlich verwendet. Die hier angegebene Definition orientiert sich an den Büchern von Diestel und Lovász u.a. Aigner und Kőnig sprechen in ihren Büchern hingegen von Kantenfolgen. Kőnig benutzt den Begriff Kantenzug, um deutlich zu machen, dass sich keine Kanten wiederholen. Mitunter wird auch der Begriff Weg für Kantenzug benutzt (Steger). Auch in der englischsprachigen Literatur wird der Begriff nicht einheitlich benutzt, er wird gelegentlich mit walk bezeichnet, mitunter aber auch als path bezeichnet.
A-B-Weg, v-w-Weg, a-B-Fächer
Sind
und
Teilmengen von der
Knotenmenge
eines Graphen, so bezeichnet man einen Weg als
-
-Weg,
falls einer seiner Endknoten in
und der andere in
liegt. Statt von einem
-
-Weg
spricht man auch von einem
-
-Weg.
Eine Menge von
-
-Wegen
nennt man einen
-
-Fächer,
wenn die Wege paarweise nur den Knoten
gemeinsam haben.
Disjunkte Wege
Zwei Wege
und
in einem Graphen heißen kreuzungsfrei, knotendisjunkt oder einfach
nur disjunkt, wenn es kein Paar
mit
aus
und
aus
gibt, für das
ist, sie also keine inneren Knoten gemeinsam haben.
Eine Menge von Wegen nennt man kreuzungsfrei, knotendisjunkt oder disjunkt, wenn die Wege paarweise disjunkt sind.
Eine Menge disjunkter Wege in einem Graphen mit der Eigenschaft, dass jeder Knoten des Graphen auf einem dieser Wege liegt, heißt Wegüberdeckung des Graphen.
Länge und Abstand
In Graphen ohne Gewichte auf den Kanten bezeichnet man mit der Länge eines Weges oder Kantenzuges die Anzahl seiner Kanten. In kantengewichteten Graphen bezeichnet man als Länge eines Weges die Summe der Kantengewichte aller zugehörigen Kanten. Die Länge des längsten Weges in einem Graphen nennt man Umfang des Graphen.
Als einen kürzesten
Weg von einem Knoten
zu einem Knoten
in einem Graphen bezeichnet man einen Weg von
nach
,
dessen Länge minimal ist. Die Länge eines kürzesten Weges nennt man dann
Abstand oder Distanz von
nach
.
Die Exzentrizität eines Knotens
ist der maximale Abstand zu allen anderen Knoten
des Graphen. Der Rand eines Graphens ist die Menge der Knoten mit
maximaler Exzentrizität. Man beachte, dass in gerichteten Graphen der Abstand
von der Richtung des Weges abhängt. Insbesondere kann es sein, dass nur in eine
Richtung ein gerichteter Weg existiert.
Den größten Abstand zwischen zwei Knoten in einem Graphen
nennt man den Durchmesser
des Graphen. Der Durchmesser ist damit das Maximum aller Exzentrizitäten der
Knoten in
.
Der Radius
eines Graphen ist das Minimum der Exzentrizitäten seiner Knoten. Für alle
Graphen
gilt
.
Die Knoten, deren Exzentrizität dem Radius entsprechen, bilden das Zentrum des Graphen.
Distanzgraph
Der Distanzgraph zu einem Graphen
bezeichnet den vollständigen
(das heißt je zwei Knoten sind durch eine Kante verbunden, ggf. in gerichteten
Graphen in beide Richtungen, wobei es aber keine Schleifen gibt)
kantengewichteten Graphen auf der Knotenmenge
,
der jeder Kante als Kantengewicht den Abstand zwischen den beiden Knoten in
zuordnet.
Literatur
- Reinhard Diestel: Graphentheorie, 3. neu bearb. und erw. Auflage, Springer, Berlin, 2006, ISBN 3-540-21391-0
- László Lovász, Jósef Pelikán, Katalin Vesztergombi: Diskrete Mathematik, Springer, Berlin, 2003, ISBN 0-387-95584-4
- Dénes Kőnig: Theorie der endlichen undunendlichen Graphen. Akademische Verlagsgesellschaft, Leipzig 1936
- Angelika Steger: Diskrete Strukturen, 2. Auflage, Band 1: Kombinatorik, Graphentheorie, Algebra, Springer, Berlin, 2007, ISBN 978-3-540-46660-4


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.06. 2021