
Basiswechsel (Vektorraum)
Der Basiswechsel oder die Basistransformation ist ein Begriff
aus dem mathematischen
Teilgebiet der linearen
Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen
eines endlichdimensionalen Vektorraums
über einem Körper
.
Dadurch ändern sich im Allgemeinen die Koordinaten der Vektoren und die Abbildungsmatrizen von
linearen
Abbildungen. Ein Basiswechsel ist somit ein Spezialfall einer Koordinatentransformation.
Der Basiswechsel kann durch eine Matrix beschrieben werden, die Basiswechselmatrix, Transformationsmatrix oder Übergangsmatrix genannt wird. Mit dieser lassen sich auch die Koordinaten bezüglich der neuen Basis ausrechnen. Stellt man die Basisvektoren der alten Basis als Linearkombinationen der Vektoren der neuen Basis dar, so bilden die Koeffizienten dieser Linearkombinationen die Einträge der Basiswechselmatrix.
Basiswechselmatrix
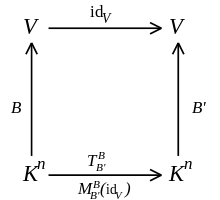
Es sei
ein
-dimensionaler
Vektorraum über dem Körper
(zum Beispiel dem Körper
der reellen Zahlen). In
seien zwei geordnete Basen gegeben,
und
.
Die Basiswechselmatrix
für den Basiswechsel von
nach
ist eine
-Matrix.
Es handelt sich um die Abbildungsmatrix
der Identitätsabbildung
auf
bezüglich der Basen
im Urbild und
im Bild:
Man erhält sie, indem man die Vektoren der alten Basis
als Linearkombinationen der Vektoren der neuen Basis
darstellt:
Die Koeffizienten
bilden die
-te
Spalte der Basiswechselmatrix
Diese Matrix ist quadratisch und invertierbar
und somit ein Element der allgemeinen
linearen Gruppe .
Ihre Inverse
beschreibt den Basiswechsel von
zurück nach
.
Spezialfälle
Ein wichtiger Spezialfall ist der Fall ,
der Vektorraum stimmt also mit dem Koordinatenraum
überein. In diesem Fall sind die Basisvektoren Spaltenvektoren
die sich zu Matrizen
zusammenfassen lassen, die hier der Einfachheit halber mit den gleichen Buchstaben wie die zugehörigen Basen bezeichnet werden. Die Bedingung
übersetzt sich dann zu
das heißt,
Die Transformationsmatrix
lässt sich somit durch
berechnen, wobei
die inverse
Matrix der Matrix
ist.
Insbesondere gilt: Ist
die Standardbasis, so gilt
.
Ist
die Standardbasis, so gilt
.
Wie im Vorangehenden wird hier die Basis
mit der Matrix identifiziert, die man erhält, indem man die Basisvektoren als
Spaltenvektoren schreibt und diese zu einer Matrix zusammenfasst.
Koordinatentransformation
Ein Vektor
habe bezüglich der Basis
die Koordinaten
,
d.h.
und bezüglich der neuen Basis
die Koordinaten
,
also
Stellt man wie oben die Vektoren
der alten Basis als Linearkombination der neuen Basis dar, so erhält man
Dabei sind die
die oben definierten Einträge der Basiswechselmatrix
.
Durch Koeffizientenvergleich erhält man
bzw. in Matrizenschreibweise:
oder kurz:
Basiswechsel bei Abbildungsmatrizen
Die Darstellungsmatrix einer linearen Abbildung hängt von der Wahl der Basen im Urbild- und im Zielraum ab. Wählt man andere Basen, so erhält man auch andere Abbildungsmatrizen.
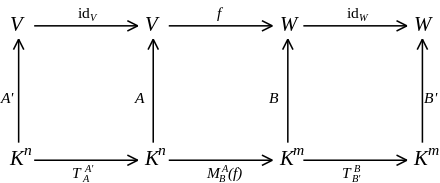
Seien
ein
-dimensionaler
und
ein
-dimensionaler
Vektorraum über
und
eine lineare Abbildung. In
seien die geordneten Basen
und
gegeben, in
die geordneten Basen
und
.
Dann gilt für die Darstellungsmatrizen von
bezüglich
und
bzw. bezüglich
und
:
Man erhält diese Darstellung, indem man
schreibt. Die Abbildungsmatrix der Verkettung ist dann das Matrizenprodukt der
einzelnen Abbildungsmatrizen, wenn die Basen passend gewählt sind, das heißt:
die Basis
im Urbild von
,
die Basis
im Bild von
und im Urbild von
,
die Basis
im Bild von
und im Urbild von
,
und die Basis
im Bild von
.
Man erhält also:
Ein wichtiger Spezialfall ist, wenn
ein Endomorphismus
ist und im Urbild und Bild jeweils dieselbe Basis
bzw.
benutzt wird. Dann gilt:
Setzt man ,
so gilt also
Die Abbildungsmatrizen
und
sind also ähnlich.
Beispiel
Wir betrachten zwei Basen
und
des
mit
und
wobei die Koordinatendarstellung der Vektoren die Vektoren bezüglich der Standardbasis beschreibt.
Die Transformation der Koordinaten eines Vektors
ergibt sich durch die Darstellung der alten Basisvektoren
bezüglich der neuen Basis
und deren Gewichtung mit
.
Um die Matrix der Basistransformation
von
nach
zu berechnen, müssen wir die drei linearen
Gleichungssysteme
nach den 9 Unbekannten
auflösen.
Dies kann mit dem Gauß-Jordan-Algorithmus für alle drei Gleichungssysteme simultan erfolgen. Dazu wird folgendes lineares Gleichungssystem aufgestellt:
Durch Umformen mit elementaren Zeilenoperationen lässt sich die linke Seite auf die Einheitsmatrix bringen und auf der rechten Seite erhält man als Lösung des Systems die Transformationsmatrix
.
Wir betrachten den Vektor ,
also den Vektor der bezüglich der Basis
die Koordinaten
besitzt. Um nun die Koordinaten bezüglich
zu berechnen, müssen wir die Transformationsmatrix
mit diesem Spaltenvektor multiplizieren:
.
Also ist .
In der Tat rechnet man als Probe leicht nach, dass
gilt.
Basiswechsel mit Hilfe der dualen Basis
Im wichtigen und anschaulichen Spezialfall des euklidischen
Vektorraums (V, ·) kann der Basiswechsel elegant mit der dualen Basis
einer Basis
durchgeführt werden. Für die Basisvektoren gilt dann
mit dem Kronecker-Delta
.
Skalare Multiplikation eines Vektors
mit den Basisvektoren
,
Multiplikation dieser Skalarprodukte mit den Basisvektoren
und Addition aller Gleichungen ergibt einen Vektor
Hier wie im Folgenden ist die Einsteinsche
Summenkonvention anzuwenden, der zufolge über in einem Produkt doppelt
vorkommende Indizes, im vorhergehenden Satz beispielsweise nur
,
von eins bis
zu summieren ist. Skalare Multiplikation von
mit irgendeinem Basisvektor
ergibt wegen
dasselbe Ergebnis wie die skalare Multiplikation von
mit diesem Basisvektor, weswegen die beiden Vektoren identisch sind:
Analog zeigt sich:
Dieser Zusammenhang zwischen den Basisvektoren und einem Vektor, seinen Komponenten und Koordinaten, gilt für jeden Vektor im gegebenen Vektorraum.
Wechsel zur dualen Basis
Skalare Multiplikation beider Gleichungen mit
liefert
oder
Die Umkehroperation mit
ist
Für die oben benutzten Skalarprodukte
und
gilt:
Wechsel zu einer anderen Basis
Gegeben sei ein Vektor ,
der von einer Basis
zur Basis
wechseln soll. Das gelingt, indem jeder Basisvektor gemäß
durch die neue Basis ausgedrückt wird:
mit
Die Umkehrung davon ist
Der Basiswechsel bei Tensoren zweiter Stufe wird analog durchgeführt:
mit
was sich ohne weiteres auf Tensoren höherer Stufe verallgemeinern lässt. Das
Rechenzeichen „“
bildet das dyadische
Produkt.
Der Zusammenhang zwischen den Koordinaten
und
kann kompakt mit Basiswechselmatrizen
mit den Komponenten
bei einem Basiswechsel von
nach
und ihren dualen Partnern dargestellt werden. Die Inverse der
Basiswechselmatrix hat, wie oben angedeutet, die Komponenten
denn bei der Matrizenmultiplikation ergibt sich für Komponenten
:
Anwendungen
Basiswechselmatrizen besitzen vielfältige Anwendungsmöglichkeiten in der Mathematik und Physik.
In der Mathematik
Eine Anwendung von Basiswechselmatrizen in der Mathematik ist die Veränderung der Gestalt der Abbildungsmatrix einer linearen Abbildung, um die Rechnung zu vereinfachen.
Möchte man zum Beispiel die Potenz
einer
-Matrix
mit einem Exponenten
berechnen, so ist die Zahl der benötigten Matrizenmultiplikationen von der
Größenordnung
.
Ist
diagonalisierbar, so existieren eine Diagonalmatrix
und eine Basiswechselmatrix
,
sodass
und somit
Die Zahl der für die Berechnung der rechten Seite benötigten Multiplikationen ist nur von der Größenordnung:
zur Berechnung von
,
zur Berechnung des Produkts
- sowie einer Matrixmultiplikation für das Produkt
Da die Matrixmultiplikation
von der Größenordnung
ist, erhalten wir eine Komplexität von
anstelle von
.
In der Physik
Eine Anwendung von Basiswechselmatrizen in der Physik findet bspw. in der Ähnlichkeitstheorie statt, um dimensionslose Kennzahlen zu ermitteln. Hierbei werden durch einen Basiswechsel einer physikalischen Größe neue Basisdimensionen zugeordnet. Die dimensionslosen Kennzahlen stellen dann genau das Verhältnis der physikalischen Größe zu seiner Dimensionsvorschrift dar.
Literatur
- Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen. Springer Spektrum, Berlin/Heidelberg 2013, ISBN 978-3-642-32185-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.10. 2021