Quasikörper

Ein Quasikörper, nach Oswald Veblen und Joseph Wedderburn auch Veblen-Wedderburn-System genannt, ist eine algebraische Struktur, die in der synthetischen Geometrie als Koordinatenbereich für bestimmte affine Ebenen, die affinen Translationsebenen dient. Quasikörper sind stets kartesische Gruppen und jeder Alternativkörper ist ein Quasikörper.

Definitionen

Bei der geometrischen Definition wird auf einer affinen Translationsebene durch Wahl einer Punktbasis (O,E_1,E_2) ein affines Koordinatensystem eingeführt. Dabei dienen die Punkte auf der ersten Achse $OE_{1}$ dieses Koordinatensystems als Koordinaten. Auf dem Koordinatenbereich $K=OE_{1}$ werden eine Addition und Multiplikation durch geometrische Konstruktion eingeführt.

Bei der algebraischen Definition wird der Quasikörper $(K,+,\cdot)$ durch seine algebraischen Eigenschaften charakterisiert und auf der Menge der Paare $K^{2}$ als Punktkoordinaten eine affine Translationsebene durch algebraische Gleichungen, die die Geraden beschreiben, aufgebaut.

Geometrische Definition

Eine affine Ebene heißt affine Translationsebene, wenn es zu jedem Paar von Punkten $(P,Q)\in A^{2}$ eine Translation $\tau =\overrightarrow {PQ}$ gibt, also eine Kollineation $\tau :A\rightarrow A$ mit den Eigenschaften

$\tau (P)=Q$ ,
für jede Gerade der Ebene ist $\tau (g)\parallel g$ ,
$\tau$ ist die Identität oder fixpunktfrei.

Eine affine Ebene ist genau dann eine Translationsebene, wenn in ihr der kleine affine Satz von Desargues gilt.

In der affinen Translationsebene werden drei verschiedene Punkte $O,E_{1},E_{2}$ gewählt, die nicht auf einer gemeinsamen Gerade liegen. Die Punkte der ersten Koordinatenachse $K=OE_{1}$ dienen als Koordinaten. Jedem Punkt der Ebene kann durch die Koordinatenkonstruktion ein Paar $(x_{1},x_{2})\in K^{2}$ umkehrbar eindeutig zugeordnet werden.

Addition

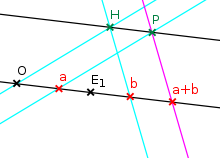
Addition von zwei Elementen $a,b\in K=OE_{1}$ . Die Summe

ist unabhängig von der Lage des Hilfspunktes

Seien $a,b\in K$ zwei Punkte auf der ersten Koordinatenachse $OE_{1}$ . Deren Summe a+b erhält man wieder als Punkt auf dieser Achse durch folgende Konstruktion, vergleiche dazu die Abbildung rechts:

Wähle einen Hilfspunkt außerhalb der ersten Koordinatenachse.
Die Parallele zu $OE_{1}$ durch schneidet die Parallele zu durch in .
Die Parallele zu durch schneidet die erste Koordinatenachse $OE_{1}$ im Punkt . Dieser Punkt ist die gesuchte Summe.

Das Ergebnis der Konstruktion ist unabhängig davon, welchen Hilfspunkt außerhalb der ersten Koordinatenachse man verwendet. Vom zugrundegelegten Koordinatensystem gehen nur der Ursprung und die erste Koordinatenachse als Gerade in die Konstruktion ein. Das heißt: Wählt man ein anderes Koordinatensystem mit demselben Ursprung und derselben ersten Koordinatenachse, aber einen anderen ersten Einheitspunkt auf dieser Achse und einen beliebigen zweiten Einheitspunkt außerhalb der ersten Achse, dann ändert sich dadurch die Addition nicht.

Durch die so konstruierte Addition wird (K,+) zu einer kommutativen Gruppe. Ihr neutrales Element ist der Ursprung des Koordinatensystems. Sie ist zur Gruppe der Parallelverschiebungen in Richtung der ersten Koordinatenachse isomorph – und damit zu jeder Gruppe von Parallelverschiebungen der Ebene in eine feste Richtung.

Multiplikation

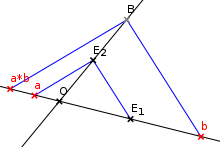
Multiplikation von zwei Elementen $a,b\in K$ .

Seien $a,b\in K$ zwei Punkte auf der ersten Koordinatenachse $OE_{1}$ . Deren Produkt $a\cdot b$ erhält man wieder als Punkt auf dieser Achse durch folgende Konstruktion, vergleiche dazu die Abbildung rechts:

Die Parallele zu $E_{1}E_{2}$ durch schneidet die zweite Koordinatenachse $OE_{2}$ in .
Die Parallele zu $aE_{2}$ durch schneidet die erste Koordinatenachse $OE_{1}$ im Punkt $a\cdot b$ . In der Zeichnung ist dieser Punkt aus technischen Gründen mit beschriftet.

Mit den beiden Verknüpfungen Addition und Multiplikation erfüllt die erste Koordinatenachse $K=OE_{1}$ die nachfolgend genannten algebraischen Eigenschaften eines Quasikörpers. Das neutrale Element der Multiplikation ist der erste Einheitspunkt $1=E_{1}$ .

Algebraische Definition

Eine Menge mit den zweistelligen Verknüpfungen $+,\;\cdot$ und zwei verschiedenen Strukturkonstanten $0,1\in K$ heißt (Links-)Quasikörper, wenn die folgenden Axiome gelten:

ist eine abelsche Gruppe mit neutralem Element 0.
$(K\setminus \lbrace 0\rbrace ,\cdot )$ ist eine Loop mit dem neutralen Element 1, also eine Quasigruppe mit einem zugleich links- und rechtsneutralen Element 1.
$a\cdot 0=0\cdot a=0$ gilt für alle $a\in K$ .
Es gilt das Linksdistributivgesetz: $a\cdot (b+c)=a\cdot b+a\cdot c$ für alle $a,b,c\in K$ .
Zu $a,b,c\in K$ mit $a\neq b$ gibt es genau ein $y\in K$ mit $a\cdot y-b\cdot y=c$ .

Erfüllt die Struktur $(K,+,\cdot)$ diese Eigenschaften eines Quasikörpers, dann können auf der durch die Menge der Paare $A=K^{2}$ gegebenen Punktmenge durch Koordinatengleichungen Geraden definiert werden. Die Struktur aus Punkten und Geraden bildet dann eine affine Translationsebene. → Die Geradengleichungen sind im Artikel Ternärkörper im Abschnitt Geometrie der Ebene beschrieben.

Kern eines Quasikörpers

Die Menge

$\operatorname {Kern}(K)=\lbrace x\in K:\;\forall a,b\in K\left((a+b)x=ax+bx\land (ab)x=a(bx)\right)\rbrace$

wird als Kern des Quasikörpers bezeichnet. Dieser Kern ist ein Schiefkörper. Der Quasikörper ist ein Modul über seinem Kern.

Eigenschaften und Bemerkungen

Der durch die Axiome definierte Quasikörper ist genauer ein Linksquasikörper, denn in ihm gilt das Linksdistributivgesetz. Auch Rechtsquasikörper – mit Rechtsdistributivgesetz statt 4. und entsprechend mit umgekehrter Multiplikation formuliertem 5. Axiom – werden in der Literatur einfach als Quasikörper gezeichnet, hier kommen aber auch die qualifizierten Begriffe vor.^[1]
Ein Quasikörper, in dem beide Distributivgesetze gelten, wird in der Geometrie als Halbkörper bezeichnet. Man beachte aber, dass diese Bezeichnung in der Mathematik nicht einheitlich gebraucht wird und vergleiche dazu Halbkörper.
Offensichtlich wird ein Linksquasikörper durch Umkehrung der Multiplikation zu einem Rechtsquasikörper und umgekehrt.
Gilt in einem Halbkörper im Sinne der synthetischen Geometrie zusätzlich zu beiden Distributivgesetzen die Alternativität, eine abgeschwächte Form des Assoziativgesetzes der Multiplikation, dann ist dieser Halbkörper sogar ein Alternativkörper.
Durch die Definition $T(a,b,c)=a\cdot b+c$ kann auf jedem Quasikörper eine Ternärverknüpfung eingeführt werden, mit der der Quasikörper zu einem linearen Ternärkörper wird.
Zum 5. Axiom des Quasikörpers in der algebraischen Definition ist zu bemerken:

Gilt in auch das Rechtsdistributivgesetz, dann folgt das 5. Axiom aus den ersten drei Axiomen, es ist eine echte Abschwächung des Rechtsdistributivgesetzes.
Es ist entbehrlich, das heißt, es folgt ohne weitere Voraussetzungen aus den übrigen Axiomen, falls endlich ist.

Quasikörper wurden bis 1975 in der Literatur als Veblen-Wedderburn-System bezeichnet.
Jeder Quasikörper ist eine kartesische Gruppe.
Jeder Fastkörper ist ein Quasikörper. Ein Quasikörper ist genau dann ein Fastkörper, wenn seine Multiplikation assoziativ ist.

Quasikörper als Koordinatenbereiche projektiver Ebenen

Quasikörper treten auch als Koordinatenbereiche von speziellen projektiven Ebenen auf. Dies sind in der Klassifikation projektiver Ebenen nach Hanfried Lenz die Ebenen der Klassen IV, V und VII.

Genauer gilt: Eine projektive Ebene der Klasse IVa bzw. IVb lässt sich durch Wahl einer geeigneten Punktbasis durch einen Linksquasikörper bzw. einen Rechtsquasikörper koordinatisieren. Jeder Ternärkörper, der der Ebene bei Wahl einer beliebigen Punktbasis zugeordnet wird, ist isotop zu einem Links- bzw. Rechtsquasikörper.
Alle Koordinatenbereiche einer projektiven Ebene der Klasse V sind zueinander isotope Halbkörper, also zugleich Rechts- und Linksquasikörper. Im Allgemeinen sind diese Halbkörper aber nicht zueinander isomorph.
Alle Koordinatenbereiche einer projektiven Ebene der Klasse VII sind zueinander isomorphe Alternativkörper.

Beispiele

Jede stärkere algebraische Struktur, also jeder Fastkörper, Alternativkörper, Schiefkörper oder Körper liefert ein Beispiel für einen Quasikörper.
Der Artikel Ternärkörper enthält einige Beispiele für Quasikörper, insbesondere auch ein ausführlich dargestelltes Beispiel eines endlichen, nichtkommutativen Quasikörpers (→ im Unterabschnitt Beispiele der Ordnung 9).
Quasikörper endlicher Moulton-Ebenen

Die endlichen Moulton-Ebenen haben als Koordinatenbereich „echte“ Quasikörper. Zur Konstruktion geht man von einem endlichen Körper aus, dessen Charakteristik eine ungerade Primzahl ist. In der zyklischen, multiplikativen Gruppe $F^{\ast }=F\setminus \lbrace 0\rbrace$ existiert dann genau eine Untergruppe vom Index 2, das ist die Untergruppe der Quadrate $Q_{1}=(F^{\ast })^{2}=\lbrace x^{2}:x\in F^{\ast }\rbrace$ . Sei $\varphi$ ein Körperautomorphismus von . Nun wird eine neue Multiplikation $\odot :F\times F\rightarrow F$ eingeführt:

$a\odot b={\begin{cases}a\cdot b\quad {\mathrm {falls}}\;a\in Q_{1}\\a\cdot \varphi (b)\quad {\mathrm {falls}}\;a\not \in Q_{1}.\end{cases}}$

Damit wird $(F,+,\odot ,0,1)$ zu einem Linksquasikörper, denn das Linksdistributivgesetz ist erfüllt. Wenn der gewählte Körperautomorphismus $\varphi$ nicht die Identität ist, dann ist
1. das Kommutativgesetz für die Verknüpfung $\odot$ nicht erfüllt,
2. das Assoziativgesetz für die Verknüpfung $\odot$ genau dann erfüllt, wenn $\varphi$ involutorisch ist, also $\varphi ^{2}={\mathrm {Id_{F}}}$ gilt (genau dann ist F mit der neuen Multiplikation ein Linksfastkörper),
3. das Rechtsdistributivgesetz nicht erfüllt, da stets Elemente $a,b\in Q_{1}$ mit $a+b\not \in Q_{1}$ existieren.
4. Das 5. Axiom für Quasikörper folgt aus den übrigen Axiomen, da endlich ist.
5. $(F\setminus \{0\},\odot ,1)$ ist eine Loop: Die Neutralität des Einselementes der „gewöhnlichen“ Körpermultiplikation auch bezüglich $\odot$ ist offensichtlich. Die Lösungen der Gleichungen $a\odot x=b$ und $y\odot a=b$ , $(a,b\in F\setminus \{0\})$ lauten
$x=a\operatorname {\setminus }b={\begin{cases}a^{{-1}}\cdot b\,&(a\in Q_{1})\\\varphi ^{{-1}}(a^{{-1}}\cdot b)\,&(a\not \in Q_{1})\end{cases}}\quad {\mathrm {bzw.}}\;y=b/a={\begin{cases}b\cdot a^{{-1}}\,&(a\cdot b\in Q_{1})\\b\cdot \varphi (a^{{-1}})\,&(a\cdot b\not \in Q_{1})\end{cases}}$

Der Kern des Quasikörpers $(F,+,\odot ,0,1)$ ist der vom Körperautomorphismus $\varphi$ fixierte endliche Teilkörper $S=\{x\in F:\varphi (x)=x\}$ von .

Literatur
- Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. In: Mathematik für das Lehramt an Gymnasien. 1. Auflage. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.
- Charles Weibel: Survey of Non-Desarguesian Planes. In: Notices of the American Mathematical Society. Band 54. American Mathematical Society, November 2007, S. 1294–1303
Anmerkungen
1. ↑ Weibel (2007) formuliert explizit Axiome „(for) a (right) quasi-field “, nennt diesen ansonsten einfach „quasi-field“. Er erwähnt (S. 1300), dass „(for) a left quasi-field ... $R^{{op}}$ is a a right quasi-field“. Degen (1976) kennt nur eine Sorte „Quasikörper“, der das Linksdistributivgesetz erfüllt, also „left quasi-field“.
Basierend auf einem Artikel in: Wikipedia.de
Seite zurück
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2021