Kollineation

Der Begriff Kollineation bezeichnet in den mathematischen Gebieten Geometrie und lineare Algebra eine bijektive Abbildung eines affinen oder projektiven Raumes auf sich selbst, bei der jede Gerade auf eine Gerade abgebildet wird, die also geradentreu ist. Die Menge der Kollineationen eines Raumes bildet eine Gruppe, insbesondere sind die Umkehrungen von Kollineationen stets Kollineationen.

Das Bild zeigt eine Kollineation der affinen Ebene über dem Quadratischen Zahlkörper $K=\Q(\sqrt{2})$ . Obwohl eine affine Punktbasis (blaue Punkte $O,E_{1},E_{2}$ ) der Ebene durch die Kollineation fixiert wird, werden unendlich viele Punkte nicht fixiert sondern am Ursprung gespiegelt: die Punkte

und alle rationalen Linearkombinationen $(a\cdot {\sqrt {2}},b\cdot {\sqrt {2}}),a,b\in \mathbb{Q} \setminus \{0\}$ !

Damit fällt der Begriff für eindimensionale Räume mit dem Begriff der Bijektion der betreffenden Geraden zusammen. Daher werden meist nur Kollineationen auf mindestens zweidimensionalen Räumen studiert.

Gelegentlich wird der Begriff Kollineation auch für eine bijektive oder auch nur injektive geradentreue Abbildung eines affinen oder projektiven Raumes in einen anderen Raum benutzt. Der vorliegende Artikel befasst sich ausschließlich mit Kollineationen, die geradentreue, bijektive Selbstabbildungen eines Raumes sind.

→ In einem allgemeineren Sinn werden auch die Automorphismen endlicher Inzidenzstrukturen als Kollineationen bezeichnet. Siehe dazu Endliche Geometrie#Automorphismen.

Kollineationen in der synthetischen Geometrie

In der synthetischen Geometrie werden in der Regel Kollineationen auf zweidimensionalen Räumen (Ebenen) untersucht. Da für die nichtdesargueschen Ebenen die Gruppe der Affinitäten bzw. Projektivitäten oft nicht reichhaltig genug ist, um die Struktur der Ebene zu untersuchen, tritt hier die Gruppe der Kollineationen an deren Stelle. In einer abstrakten Inzidenzgeometrie bildet diese Gruppe die charakteristische Automorphismengruppe, da hier die „Lage von Punkten auf einer gemeinsamen Geraden (Kollinearität)“ die einzige Struktur auf dem Raum und damit - im Sinne des Erlanger Programms - die einzige den Raum, also hier die Ebene, charakterisierende Invariante ist.

Ebenentreue Kollineationen und geometrische Automorphismen

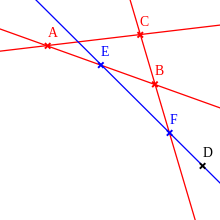
Ein Punkt D in einem Raum mit mehr als 2 Punkten auf jeder Geraden liegt genau dann in der Ebene, die durch ein Dreieck ABC bestimmt ist, wenn die Verbindungsgerade DE von D mit einem Punkt E auf der Geraden AB, der aber weder gleich A noch gleich B ist, wenigstens eine der Dreiecksseiten (Geraden!) BC oder AC in einem Punkt $F\neq E$ schneidet. Damit lässt sich für affine und projektive Geometrien mit mehr als 2 Punkten auf jeder Geraden „Ebenentreue“ auf „Geradentreue“ zurückführen.

Jede Kollineation $\kappa$ einer affinen Ebene ist parallelentreu, das heißt, für zwei Geraden der Ebene gilt $g\parallel h\Leftrightarrow \kappa (g)\parallel \kappa (h)$ .
Eine Kollineation einer mindestens dreidimensionalen affinen Geometrie ist genau dann parallelentreu, wenn sie ebenentreu ist, das heißt, wenn die Bilder von vier beliebigen komplanaren Punkten stets komplanar sind.
Eine Kollineation einer affinen Geometrie mit mehr als 2 Punkten auf jeder Geraden oder einer beliebigen projektiven Geometrie ist stets ebenentreu. Vergleiche die Abbildung rechts und das Beispiel der Ordnung 2 weiter unten.
Eine ebenentreue Kollineation ist stets ein geometrischer Automorphismus des Raumes, das heißt, sie bildet jeden Unterraum auf einen Unterraum der gleichen Dimension ab. Umgekehrt ist natürlich jeder geometrische Automorphismus eine ebenentreue Kollineation.
Eine „Bijektion durch Basiswechsel bei gleichen Koordinaten“, d. h. eine Abbildung des mindestens zweidimensionalen Punktraumes, bei der jeder Punkt auf einen Punkt mit den gleichen Koordinaten (aus einem Ternärkörper im Fall einer Ebene, aus einem Schiefkörper im Fall eines mindestens dreidimensionalen Raumes), jeder Unterraum auf einen Unterraum mit den gleichen Koordinatengleichungen abgebildet wird, aber Koordinaten und Gleichungen auf eine andere Punktbasis bezogen werden, ist eine ebenentreue Kollineation und damit ein geometrischer Automorphismus

im Falle einer mindestens zweidimensionalen affinen Geometrie,
im Falle einer mindestens dreidimensionalen projektiven Geometrie und
im Falle einer Moufangebene.

Umgekehrt existieren aber im Allgemeinen ebenentreue Kollineationen, die sich nicht durch einen Basiswechsel bei „Koordinatenidentität“ darstellen lassen.
Jede ebenentreue Kollineation einer mindestens zweidimensionalen affinen Geometrie lässt sich eindeutig zu einer Kollineation in ihrem projektiven Abschluss fortsetzen. Dort ist dann die Fernhyperebene eine Fixhyperebene der projektiven Kollineation.
Umgekehrt entspricht einer Kollineation in einer mindestens zweidimensionalen projektiven Geometrie genau dann eine ebenentreue Kollineation der affinen Geometrie, die durch Schlitzen der projektiven Geometrie entsteht, wenn längs einer Fixhyperebene der Kollineation geschlitzt wird.
Wichtig für die synthetische Geometrie, insbesondere für das Studium der nichtdesarguesschen projektiven Ebenen, sind die zentralen oder axialen Kollineationen, die ebenen Perspektivitäten. Diese Kollineationen erzeugen die Untergruppe der Projektivitäten innerhalb der Kollineationsgruppe einer projektiven Ebene. Die Projektivitäten bilden sogar einen Normalteiler dieser Kollineationsgruppe.

Kollineationen verallgemeinern geometrische Abbildungen

In der synthetischen wie in der analytischen Geometrie verallgemeinert Kollineation Abbildungsbegriffe, bei denen zusätzliche Invarianten gefordert werden:

Eine Kollineation eines beliebigen affinen Raumes endlicher Dimension , in dem jede Gerade mehr als zwei Punkte hat,^[1] ist genau dann eine Affinität, wenn sie zusätzlich teilverhältnistreu ist.
Eine Kollineation einer desargueschen affinen Ebene ist genau dann eine Affinität, wenn sie zusätzlich teilverhältnistreu ist.
Eine Kollineation einer beliebigen affinen Ebene ist genau dann eine Affinität, wenn jede ihrer Einschränkungen auf eine Gerade der Ebene sich als Komposition von endlich vielen bijektiven Parallelprojektionen darstellen lässt.
Eine Kollineation eines mindestens dreidimensionalen projektiven Raumes endlicher Dimension ist genau dann eine Projektivität, wenn sie zusätzlich doppelverhältnistreu ist.
Eine Kollineation einer desargueschen projektiven Ebene ist genau dann eine Projektivität, wenn sie zusätzlich doppelverhältnistreu ist.
Eine Kollineation einer beliebigen projektiven Ebene ist genau dann eine Projektivität, wenn sie sich als Komposition von endlich vielen projektiven Perspektivitäten darstellen lässt.

Affinitäten und Projektivitäten sind immer spezielle Kollineationen. Sie bilden in allen Fällen eine Untergruppe und sogar einen Normalteiler der Gruppe aller (ebenentreuen^[1]) Kollineationen des Raumes, sofern dieser mindestens zweidimensional ist.

Kollineationen in der linearen Algebra, Koordinatendarstellung

Kollineationen auf affinen und projektiven Räumen endlicher Dimension n>1 über einem Körper, allgemeiner sogar über einem Schiefkörper, können durch Affinitäten bzw. Projektivitäten und einen (Schief-)Körperautomorphismus $\sigma$ des Koordinatenbereiches ausgedrückt werden. In der linearen Algebra beschränkt man sich in der Regel auf kommutative Schiefkörper, also Körper als Koordinatenbereiche. Sei ein Körper oder Schiefkörper, dann gilt:

Jede Kollineation > $\kappa$ eines endlich- aber mindestens 2-dimensionalen affinen Raumes über ^[1] besitzt bezüglich eines fest gewählten affinen Koordinatensystems eine eindeutige Darstellung als Komposition $\kappa =\alpha \circ \sigma$ . Dabei wird zunächst der Automorphismus $\sigma$ auf die Koordinaten eines Punktes angewandt und anschließend die Affinität $\alpha$ auf den neuen Koordinatenvektor.
Jede Kollineation $\kappa$ eines endlich- aber mindestens 2-dimensionalen projektiven Raumes über besitzt bezüglich eines fest gewählten projektiven Koordinatensystems eine eindeutige Darstellung als Komposition $\kappa =\pi \circ \sigma$ . Dabei wird zunächst der Automorphismus $\sigma$ auf die Koordinaten eines Punktes angewandt und anschließend die Projektivität $\pi$ auf den neuen Koordinatenvektor.
Insbesondere induziert jeder nichtidentische (Schief-)Körperautomorphismus $\sigma$ von eine affine bzw. projektive Kollineation ${\mathrm {id}}_{R}\circ \sigma$ des Raumes , die vom gewählten Koordinatensystem abhängt und keine Affinität bzw. Projektivität ist.

In beiden Darstellungen ist der Automorphismus $\sigma$ unabhängig von der Wahl des Koordinatensystems. Das Teil- bzw. Doppelverhältnis von Punkten, das koordinatenunabhängig ist, wird zu $\sigma (t)$ , wenn auf die Punkte die Kollineation $\kappa$ angewendet wird.

Folgerungen

Eine Kollineation $\kappa$ eines endlichdimensionalen desarguesschen Raumes ist bereits dann eine Affinität bzw. Projektivität,

wenn die Kollineation die Teil- bzw. Doppelverhältnisse bei allen Punkten auf einer Geraden des Raumes unverändert lässt oder
wenn die Kollineation eine Fixpunktgerade hat.

Jede Kollineation $\kappa$ auf einem mindestens zweidimensionalen, desarguesschen affinen Raum A induziert eine durch $\kappa$ eindeutig bestimmte bijektive semilineare Selbstabbildung des Raumes V der Verbindungsvektoren, eines endlichdimensionalen Linksvektorraums. Daraus folgt dann, dass die Kollineation bezüglich einer fest gewählten Punktbasis von A eindeutig als $\kappa (\overrightarrow {x})=T\cdot \sigma (\overrightarrow {x})+\overrightarrow {v_{0}}$ durch eine reguläre Matrix T, den Automorphismus $\sigma$ und den Verschiebungsanteil $\overrightarrow {v_{0}}=\kappa (O)$ dargestellt werden kann.
Jede Kollineation $\kappa$ auf einem mindestens zweidimensionalen, desarguesschen projektiven Raum P induziert eine durch $\kappa$ eindeutig bestimmte bijektive semilineare Selbstabbildung des Koordinatenvektorraums V, eines endlichdimensionalen Linksvektorraums. Daraus folgt dann, dass die Kollineation bezüglich einer fest gewählten Punktbasis von P als $\kappa (\overrightarrow {x})=T\cdot \sigma (\overrightarrow {x})$ durch eine reguläre, bis auf skarare Vielfache eindeutige Matrix T und den Automorphismus $\sigma$ dargestellt werden kann.

Auch für diese Folgerungen müssen die affinen Räume über dem Körper $\mathbb{Z } /2\mathbb{Z }$ ausgenommen werden: Ist die Dimension des Raumes größer oder gleich drei, dann treffen diese Aussagen im Allgemeinen hier nicht zu!

Kollineationen in der projektiven Geometrie

Jede Kollineation eines projektiven Raumes der Dimension $\geq 2$ ist eine semilineare Abbildung. Man hat also für $dimP(V)\geq 2$

$Coll(P(V))=P\Gamma L(V)$

für die Gruppe der Kollineationen Coll(P(V)) und die projektive semilineare Gruppe $P\Gamma L(V)$ .

Beispiele

Räume mit mindestens 3 Punkten auf jeder Geraden

Die in den folgenden Beispielen betrachteten Räume sind immer affine Räume über einem Körper mit mehr als zwei Elementen^[1] bzw. projektive Räume über einem beliebigen Körper, die Dimension der Räume ist endlich, aber mindestens 2, Verhältnis bezeichnet das Teil- bzw. Doppelverhältnis:

Die Komposition der Konjugation und einer Projektivität eines komplexen projektiven Raumes wird als Antiprojektivität bezeichnet. Alle Kollineationen in den projektiven Räumen $\mathbb{C} P^{{n}}$ sind entweder Projektivitäten oder Antiprojektivitäten.
Kollineationen auf affinen oder projektiven Räumen über einem Körper , dessen einziger Automorphismus die Identität ist, sind stets Affinitäten bzw. Projektivitäten. Solche Körper sind alle Primkörper, also die Rationalen Zahlen $\mathbb {Q}$ und alle Restklassenkörper $\mathbb {Z} /p\mathbb {Z}$ mit Primzahl.

Gleiches gilt für die Kollineationen auf Räumen über den reellen Zahlen und allgemeiner für Räume über beliebigen euklidischen Körpern, denn diese Körper besitzen wie die Primkörper keine nichtidentischen Automorphismen. – Durch die Gleichwertigkeit der Aussagen „ $a\geq 0$ “ und „ $a=x^{2}$ ist lösbar“ ist ihre natürliche Anordnung eine algebraische Invariante!

Obwohl Kollineationen im Allgemeinen nicht verhältnistreu sind, bleiben Verhältnisse erhalten, die im Primkörper eines Körpers liegen. Ist die Charakteristik eines Körpers nicht 2, dann gilt zum Beispiel:

In affinen Räumen über wird die Mitte einer Strecke (im Sinne eines geordneten Punktepaars) bei jeder Kollineation auf die Mitte der Bildstrecke abgebildet,
in projektiven Räumen über bleibt die Harmonische Lage von vier kollinearen Punkten erhalten.

Räume mit zwei Punkten auf jeder Geraden

Der dreidimensionale affine Raum über dem zweielementigen Körper K. Es sind alle 8 Punkte, aber nur 14 der 28 Geraden dieses Raumes dargestellt. Die Abbildung, die die Punkte C und F (grün) vertauscht und alle 6 anderen Punkte fest lässt, ist eine Kollineation, die weder parallelentreu noch ebenentreu ist. Die Geraden CH und FH werden vertauscht (rot), während 2 der 3 anderen Parallelen ihrer jeweiligen Schar fix bleiben. Die Ebene $\{A,C,H,E\}$ wird auf die Menge $\{A,F,H,E\}$ abgebildet, die keine Ebene ist.

Jede -dimensionale affine Geometrie ( $n\geq 1$ ) mit genau zwei Punkten auf jeder Geraden ist ein affiner Raum über dem Restklassenkörper $K=\mathbb{Z } /2\mathbb{Z }$ . Dies sind für $n\geq 2$ durchweg desarguesche affine Geometrien, aber das übliche Teilverhältnis ist degeneriert, da es ja gar keine Tripel von verschiedenen kollinearen Punkten gibt. In diesen speziellen Fällen gilt:

Die Gruppe der geradentreuen Bijektionen der Punktmenge (also der Kollineationen) ist gleich der Gruppe aller Bijektionen der Punktmenge, also isomorph zur symmetrischen Gruppe $S_{{2^{n}}}$ , denn die Geradenmenge besteht genau aus allen zweielementigen Punktmengen.
Für trifft dies auch für die Gruppe der Affinitäten zu.
Für $n\geq 3$ fordert man häufig für Kollineationen zusätzlich Ebenentreue, also dass jeder zweidimensionale Unterraum der Geometrie auf einen zweidimensionalen Unterraum abgebildet werde.
Mit diesem eingeschränkten Kollineationsbegriff gilt dann:

Jede ebenentreue Kollineation ist eine Affinität im Sinne der linearen Algebra und umgekehrt.

Dagegen ist die Gruppe der Affinitäten (sie hat $2^{n}\cdot (2^{n}-2^{0})\cdot (2^{n}-2^{1})\cdots (2^{n}-2^{{n-1}})$ Elemente,Lineare Gruppe) für $n\geq 3$ eine echte Untergruppe der $S_{{2^{n}}}$ .

Einzelnachweise

↑ ^a ^b ^c ^d Die Aussagen bleiben auch im Sonderfall des Körpers $K=\mathbb{Z } /2\mathbb{Z }$ gültig, wenn man von einer „Kollineation“ in diesem Fall zusätzlich Ebenentreue verlangt, siehe die Abschnitte #Ebenentreue Kollineationen und geometrische Automorphismen und #Räume mit zwei Punkten auf jeder Geraden.

Basierend auf einem Artikel in:

Wikipedia.de