Harmonische Teilung

Harmonische Teilung: Definition

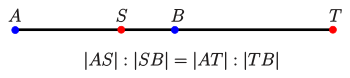
Die harmonische Teilung bezeichnet in der Geometrie ein besonderes Lageverhältnis von vier Punkten auf einer Geraden. So liegen vier Punkte A,B,S,T harmonisch, wenn die Strecke [AB] durch zwei Punkte S,T innen und außen (s. Bild) so geteilt wird, dass für die Teilstrecken die Beziehung

erfüllt ist.

Die rechte Seite kann nie 1 werden. Also darf nie der Mittelpunkt von A,B sein.
Liegt rechts von , so liegt rechts von .
Liegt links von , so liegt links von .

Die obige Gleichung und die Voraussetzung, dass die Strecke [A,B] innen und außen teilen, bedeutet, dass die beiden Teilverhältnisse (A,B;S) und (A,B;T) den gleichen Betrag haben und das Doppelverhältnis (A,B;S,T) gleich −1 ist.

Da die obige Gleichung sich auch so

schreiben lässt, teilen auch die Punkte A,B die Strecke [S,T] harmonisch. Die harmonische Teilung beschreibt also eine symmetrische Relation zwischen Punktepaaren auf einer Gerade.

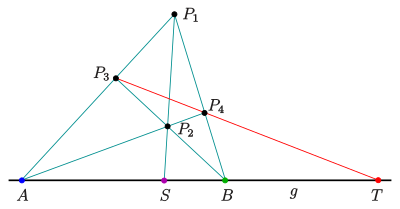
Zeichnerische Bestimmung der Teilpunkte

Mit den Strahlensätzen

Harmonische Teilung: Konstruktion mit Strahlensätzen

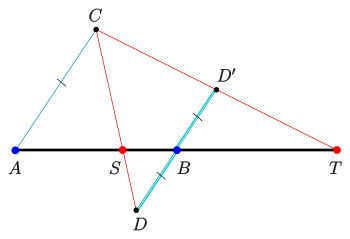
Sind die Strecke [A,B] und der Teilpunkt gegeben, so findet man den vierten harmonische Punkt (genauer: den 4. Punkt, der mit diesen 3 Punkten zusammen eine harmonische Teilung ergibt) mit Hilfe der Strahlensätze gemäß der nebenstehenden Zeichnung:

Der Punkt wird beliebig gewählt, die Geraden und sind parallel.
Der Punkt ergibt sich durch die Verbindung von mit dem gegebenen Teilpunkt .
wird nach übertragen. Die Strecken und sind gleich lang.
Der Teilpunkt ergibt sich durch den Schnitt der Geraden mit der Geraden .

Ist der Teilpunkt gegeben, verfährt man analog in umgekehrter Reihenfolge.

Ist das Teilverhältnis $\lambda$ vorgegeben, muss man den Punkt so wählen, dass $|AC|:|DB|=\lambda$ erfüllt ist. ergibt sich dann als Schnittpunkt der Gerade mit .

Mit Winkelhalbierenden eines Dreiecks

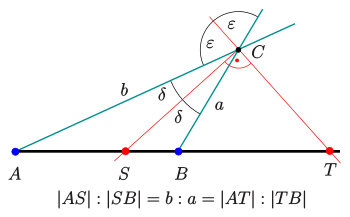
Harmonische Teilung: Konstruktion mit Winkelhalbierender eines Dreiecks

Sind A,B,C die Punkte eines nicht gleichschenkligen Dreiecks, so schneiden die Innenwinkelhalbierende und Außenwinkelhalbierende im Punkt zwei Punkte S,T aus der Geraden aus, sodass die Punkte S,T die Strecke [A,B] harmonisch im Verhältnis b:a der an anliegenden Dreiecksseiten teilen (s. Bild). Der Beweis benutzt den Satz über den Kreis des Apollonios. Man beachte, dass $a\neq b$ sein muss, s. oben.

Weitere zeichnerische Verfahren zur Bestimmungen des 4. harmonischen Punktes findet man hier.

Rechnerische Bestimmung der Teilpunkte

Rechnerisch ergibt sich die Länge der Strecke [AT] , wenn A,B und der Teilpunkt gegeben sind, aus der Formel:

$|AT|={\frac {|AS||AB|}{2|AS|-|AB|}}$ , falls der Nenner ist ( liegt rechts von )

$|AT|=-{\frac {|AS||AB|}{2|AS|-|AB|}}$ , falls der Nenner

ist ( liegt links von )

Führt man auf der Geraden durch A,B Koordinaten so ein, dass A=0,B=1,S=s,T=t ist, so ergibt sich die einheitliche Formel

$t={\frac {s}{2s-1}}.$

Beispiele harmonisch liegender Zahlen:

${\text{1)}}\ {\color {blue}0},{\color {red}{\tfrac {3}{4}}},{\color {blue}1},{\color {red}{\tfrac {3}{2}}}\ ,\quad {\text{2)}}\ {\color {blue}0},{\color {red}{\tfrac {2}{3}}},{\color {blue}1},{\color {red}2}\ ,\quad {\text{3)}}\ {\color {blue}0},{\color {red}{\tfrac {3}{5}}},{\color {blue}1},{\color {red}3}\ ,\quad {\text{4)}}\ {\color {red}-{\tfrac {1}{2}}},{\color {blue}0},{\color {red}{\tfrac {1}{4}}},{\color {blue}1}$

Beziehung zum harmonischen Mittel zweier Zahlen

Die letzte Gleichung lässt sich so umformen:

${\frac {1}{2}}\left({\frac {1}{s}}+{\frac {1}{t}}\right)=1$

D.h., das harmonische Mittel der beiden Koordinaten s,t ist gleich 1.

Verallgemeinerung

Vier Punkte einer affinen oder projektiven Gerade über einem Körper der Charakteristik $\neq 2$ liegen harmonisch, falls das Doppelverhältnis ist.

Begriffe wie zwischen, innen, außen, Längen, Abstände, die typisch für einen angeordneten Körper mit einer Metrik sind, werden bei dieser Definition nicht benötigt. Die harmonische Lage ist insbesondere also auch für die affine/projektive Gerade über den komplexen Zahlen oder einem endlichen Körper definiert.

Die obige Koordinatisierung ( A=0,B=1,S=s,T=t ) ist im affinen Fall auch über einem beliebigen Körper möglich, sodass die Beziehung $t={\tfrac {s}{2s-1}}\$ weiterhin gilt.

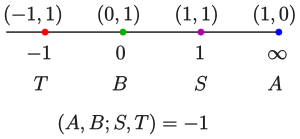
Schließt man die affine Gerade projektiv durch das Symbol $\infty$ ab und rechnet mit $\infty$ in „üblicher“ Weise, so gilt auch in diesem Fall die Formel zwischen s,t und die vier Punkte ${\color {blue}0},{\color {red}{\tfrac {1}{2}}},{\color {blue}1},{\color {red}\infty }$ liegen harmonisch, d.h. $({\color {blue}0},{\color {blue}1};{\color {red}{\tfrac {1}{2}}},{\color {red}\infty })=-1$ .

Harmonische Punktepaare: Doppelverhältnis = -1

Die Bedeutung der harmonischen Lage von vier kollinearen Punkten besteht darin, dass es immer eine involutorische projektive Abbildung der Gerade auf sich gibt, die zwei (der vier Punkte) fest lässt und die beiden anderen vertauscht. In der obigen Darstellung erzeugt die lineare Abbildung, die ${\vec {u}}$ fest lässt und ${\vec {v}}$ auf $-{\vec {v}}$ abbildet, eine solche Involution. In inhomogenen Koordinaten bewirkt sie: $\infty \to \infty ,x\to -x$ (Spiegelung am Nullpunkt). D. h.: A,B sind fix und S,T werden vertauscht.

Es gilt allgemein:

Der vierte harmonische Punkt dreier affiner Punkte, wobei einer der Mittelpunkt des restlichen Punktepaares ist, ist immer der Fernpunkt $\infty$ (s. hier).

Und:

Die harmonische Lage von vier Punkten einer projektiven Gerade ist das Analogon zum affinen Begriff Mittelpunkt zweier Punkte.

Weitere harmonische Punktepaare:

Für $A=\langle {\vec {u}}\rangle ,\ B=\langle {\vec {v}}\rangle ,\ S(s)=\langle s{\vec {u}}+{\vec {v}}\rangle ,\ T(s)=\langle s{\vec {u}}-{\vec {v}}\rangle \ ,s\neq 0$ , ist das Doppelverhältnis (A,B;S(s),T(s))=-1 .

Es gilt:

Aus folgt: . D. h., die harmonische Lage hängt nur von den beiden Punktepaaren und nicht von ihrer Anordnung ab.

Konstruktion des 4. harmonischen Punktes

Konstruktion des 4. harmonischen Punktes

Konstruktion des 4. harmonischen Punktes: $P_{1}$ ist Fernpunkt

Affine Variante der Konstruktion des 4. harmonischen Punktes: Konstruktion des Mittelpunktes M von A,B. (A,B,T sind vorgegeben)

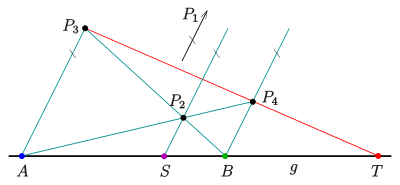
Sind drei Punkte A,B,S auf einer Geraden einer projektiven Ebene gegeben, so lässt sich der vierte harmonische Punkt mit (A,B;S,T)=-1 folgendermaßen konstruieren:

Wähle einen Punkt $P_{1}$ nicht auf .
Zeichne die Geraden $AP_{1},BP_{1},SP_{1}$ .
Wähle einen Punkt $P_{2}$ auf der Geraden $SP_{1}$ .
Die Gerade $BP_{2}$ schneidet die Gerade $AP_{1}$ in einem Punkt $P_{3}$ . Die Gerade $AP_{2}$ schneidet die Gerade $BP_{1}$ in einem Punkt $P_{4}$ .
Die Gerade $P_{3}P_{4}$ schneidet im vierten harmonischen Punkt .

Man beachte: Die Konstruktion findet in einer projektiven Ebene statt, d. h., je zwei Gerade schneiden sich.

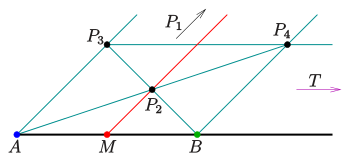
Bemerkung:

Wählt man als Punkt $P_{1}$ einen Fernpunkt und nicht auf der Ferngeraden, so sind in der Zeichenebene (affiner Teil) die Geraden $AP_{3},SP_{2},BP_{4}$ parallel (s. Bild).
Will man als vierten harmonischen Punkt zu konstruieren, so wählt man $P_{3}$ frei, $P_{4}$ auf der Geraden $P_{3}T$ und konstruiert $P_{1},P_{2}$ . ist dann der Schnittpunkt der Geraden $P_{1}P_{2}$ mit .
Sind vorgegeben und $P_{1},T$ Fernpunkte, so ergibt sich die im Bild gezeigte affine Konstruktion des Mittelpunktes zweier Punkte . ( $A,B,P_{3},P_{4}$ bilden ein Parallelogramm!)

Der Beweis der Unabhängigkeit der Konstruktion des vierten harmonischen Punktes von der Wahl der Hilfspunkte ergibt sich in der ersten affinen Variante aus den Strahlensätzen oder einfacher in der zweiten affinen Variante (Konstruktion des Mittelpunktes) daraus, dass 1) sich in einem Parallelogramm die Diagonalen halbieren und dass 2) bei Parallelprojektion der Mittelpunkt einer Strecke in den Mittelpunkt der Bildstrecke übergeht. Damit ist unabhängig von der Wahl der Punkte $P_{3},P_{4}$ .

Konstruktion des 4. harmonischen Punktes mit Hilfe eines Kreises

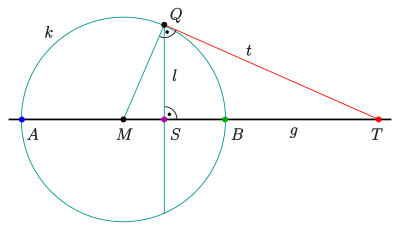
Konstruktion des 4. harmonischen Punktes: mit Kreis

Eine weitere affine Variante der Konstruktion des 4. harmonischen Punktes verwendet einen Kreis (Zirkel) und das Lotefällen (Geodreieck):
Es seien die drei affinen kollinearen Punkte A,B,S so gegeben, dass zunächst zwischen A,B liegt. Gesucht ist der 4. harmonische Punkt (außen).

Zeichne den Kreis durch , dessen Mittelpunkt auch Mittelpunkt der Punkte ist.
Errichte in die Lotgerade und schneide sie mit dem Kreis . Ein schnittpunkt sei .
Konstruiere die Tangente an den Kreis im Punkt . ( $t\perp MQ$ ).
schneidet g im 4. harmonischen Punkt .

Nähert sich einem der Punkte A,B , so auch . Ist S=M , so ist $t\parallel g$ und der Fernpunkt der Gerade .

Der Beweis ergibt sich aus der Ähnlichkeit der Dreiecke MSQ,MQT . (Man beachte, dass man nur die Gleichung |AS||TB|=|SB||AT| beweisen muss. Das Doppelverhältnis ist dann automatisch −1, da innerhalb und außerhalb der Strecke [A,B] liegt!) Aus der Ähnlichkeit folgt zunächst die Gleichung:

$|MS||MT|=r^{2}$ , wobei r der Radius des Kreises ist.

Diese Gleichung und die Konstruktionsvorschrift (s. Bild) treten auch bei der Spiegelung an einem Kreis auf. (Die Spiegelung am Einheitskreis wird mit komplexen Zahlen durch $z\to {\tfrac {1}{\overline {z}}}$ beschrieben.) Bei der Spiegelung am Kreis (s. Bild) werden die Punkte S,T vertauscht und A,B sind Fixpunkte (Jeder Punkt des Kreises bleibt fest!).

Falls der Punkt nicht zwischen den Punkten A,B liegt, konstruiert man mit Hilfe des Thaleskreises den Berührpunkt der Tangente durch an den Kreis . Das Lot von auf liefert den 4. harmonischen Punkt . (Im Bild muss man einfach und vertauschen.)

Die hier beschriebene Methode zur Konstruktion des 4. harmonischen Punktes ist ein affiner Sonderfall der folgenden Aussage:

Schneidet eine Gerade einen nichtausgearteten projektiven Kegelschnitt in zwei Punkten und ist ein von verschiedener Punkt der Geraden , so ist der zu gehörige 4. harmonische Punkt der Schnittpunkt der Polaren zu (bzgl. ) mit .

Siehe auch

Kreis des Apollonios

Basierend auf einem Artikel in:

Wikipedia.de