
Kreisspiegelung
Die Spiegelung am Kreis oder Kreisspiegelung ist eine Abbildung der ebenen Geometrie, die das Innere und das Äußere eines gegebenen Kreises miteinander vertauscht.
Die Abbildung ist winkeltreu und zählt zu den speziellen konformen Transformationen.
Eine Kreisspiegelung ist der ebene Fall einer (geometrischen) Inversion. Eine Inversion im Raum ist die Spiegelung an einer Kugel, kurz Kugelspiegelung, mit ähnlichen Eigenschaften wie die der Kreisspiegelung.
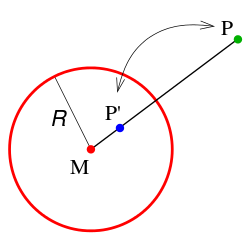
Definition
Für die Kreisspiegelung an einem Kreis mit Mittelpunkt
und Radius
ist der Bildpunkt
eines Punktes
dadurch festgelegt, dass
auf einer Strecke
bzw. auf einer Halbgeraden
liegen und die Bedingung
erfüllen muss.
Dabei darf der ursprüngliche Punkt
nicht mit dem Mittelpunkt
übereinstimmen. Gelegentlich umgeht man dieses Problem, indem man einen neuen
Punkt zur Ebene hinzufügt und diesen als Bildpunkt von
definiert. Der Bildpunkt dieses neuen Punktes ist der Mittelpunkt des
Inversionskreises. Häufig ist nur der Mittelpunkt
nicht jedoch der Radius
wichtig, sodass man einen Kreis mit beliebigem Radius (z.B. 1) zeichnen
kann.
Analytische Beschreibung
Ist in einem kartesischen
Koordinatensystem
der Ursprung, so lässt sich die Spiegelung an dem Kreis
durch
beschreiben.
In ebenen Polarkoordinaten
besitzt eine Kreisspiegelung eine besonders einfache Darstellung:
.
Die Spiegelung am Einheitskreis ist dann
und rechtfertigt die Bezeichnung Inversion.
In der Funktionentheorie
behandelt man die Inversionen und die von ihnen erzeugten
Kreisverwandtschaften am besten in der komplexen
(„Gaußschen“) Zahlenebene. Eine Inversion am Einheitskreis
wird dabei durch die Abbildung
beschrieben.
Darin bezeichnet
eine komplexe Zahl und
die zugehörige konjugiert komplexe Zahl.
Konstruktion
Mit Zirkel und Lineal
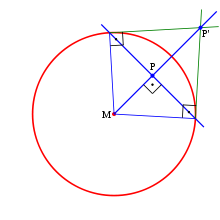
- Liegt
auf dem gegebenen Kreis, so ist
gleich
.
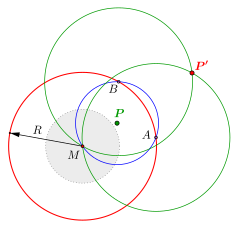
- Falls der Punkt
im Kreisinneren liegt (Bild 1), zeichnet man die zur Halbgeraden
senkrechte Kreissehne durch
und die beiden Kreistangenten in den Endpunkten dieser Sehne.
ergibt sich dann als Schnittpunkt dieser Tangenten.
- Liegt der Punkt
dagegen außerhalb des Kreises, so beginnt man mit den beiden Kreistangenten durch
mithilfe des Thaleskreises. Anschließend bringt man die Verbindungsstrecke der beiden Berührpunkte mit der Halbgeraden
zum Schnitt. Der Schnittpunkt ist der gesuchte Bildpunkt
.
Der Beweis, dass man so den Bildpunkt erhält, folgt direkt aus dem Kathetensatz.
Mit Zirkel allein
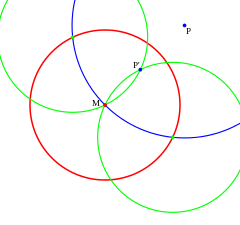
Liegt der Punkt
außerhalb des Inversionskreises (Bild 2), so zeichnet man um
einen Kreis durch den Mittelpunkt des Inversionskreises. Dieser schneidet den
Inversionskreis in zwei Punkten. Zeichne auch um diese Punkte Kreise durch den
Mittelpunkt. Diese beiden Kreise schneiden sich nun im Bildpunkt
.
Liegt
auf dem Inversionskreis, so ist keine Konstruktion notwendig, es gilt
Liegt
innerhalb des Inversionskreises, kann z.B. mithilfe einer
Einteilung der möglichen Lagen des Punktes
in drei Bereiche (Bild 3–5), eine deutliche Vereinfachung des
Konstruktionsaufwandes für zwei Bereiche erreicht werden. Hierfür stellt man
sich, quasi gedanklich, eine Kreisfläche (hellgrau) vor, deren Radius gleich ist
dem halben Radius des Inversionskreises. Für die eigentliche Konstruktion ist
die Kreisfläche (hellgrau) nicht erforderlich. Die drei Bereiche der möglichen
Lage des Punktes
,
meist gegeben als Abstand
zum Mittelpunkt
des Inverskreises, und die dafür möglichen Konstruktionsmethoden sind:
- Der Abstand des Punktes
zu
(Bild 3) ist größer als der halbe Radius des Inversionskreises, d.h.
-
- Die Beschreibung für die Konstruktion kann aus der obigen Konstruktion
für Liegt der Punkt
außerhalb des Inversionskreises (Bild 2) entnommen werden.
- Die Beschreibung für die Konstruktion kann aus der obigen Konstruktion
für Liegt der Punkt
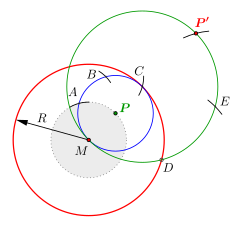
- Der Abstand des Punktes
zu
(Bild 4) ist gleich dem halben Radius des Inversionskreises, d.h.
-
- Zuerst wird um den Punkt
ein Kreis mit Radius
gezogen und anschließend, mittels dreimaligem Abtragen dieses Radius ab dem Punkt
, sein Durchmesser
bestimmt. Als Nächstes wird der letzte Kreis mit dem Radius
um den Punkt
gezogen. Abschließend bedarf es noch eines zweimaligen Abtragens dieses Radius, ab den soeben erzeugten Schnittpunkt
um den Bildpunkt
zu erhalten.
- Zuerst wird um den Punkt
- Der Abstand des Punktes
zu
(Bild 5) ist kleiner als die Hälfte, aber größer als ein Achtel des Radius des Inversionskreises, d.h.
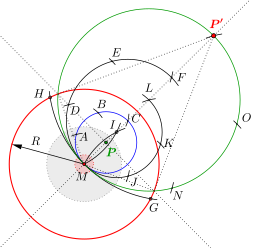
-
- Im nebenstehenden Bild 5, veranschaulicht die kleine Kreisfläche (rosa) ein Achtel des Radius des Inversionskreises. Für die eigentliche Konstruktion ist die Kreisfläche (rosa) nicht erforderlich. Dies gilt ebenso für die eingezeichneten gepunkteten Linien; sie sollen lediglich einen Vergleich mit der Konstruktion Mit Zirkel und Lineal verdeutlichen.
- Zuerst wird um den Punkt
ein Kreis mit Radius
gezogen und anschließend, durch ein dreimaliges Abtragen dieses Radius, sein Durchmesser
bestimmt. Es folgt ein Kreisbogen um
mit Radius
auf dem, analog zuvor, der Durchmesser
erzeugt wird. Nun wird ein Kreisbogen um
mit Radius
gezogen, der den Inversionskreis in
und
schneidet. Je ein Kreisbogen um
und
mit den Radien
bzw.
schließen sich an und schneiden sich in
Um
wird ein Kreisbogen mit Radius
gezogen auf dem, analog zuvor, der Durchmesser
erzeugt wird. Als Nächstes wird der letzte Kreis mit dem Radius
um den Punkt
gezogen. Abschließend bedarf es noch eines dreimaligen Abtragens dieses Radius, ab dem Punkt
um den Bildpunkt
zu erhalten.
- Universelle Methode für Liegt
innerhalb des Inversionskreises:
- Zunächst halbiert man den Radius des Inversionskreises so oft, bis man
einen neuen Kreis erhält, der den Punkt
nicht mehr enthält. (Dies ist mit Zirkel allein möglich.) Anschließend konstruiert man wie oben (Bild 2) den Bildpunkt von
, wobei die Inversion am neuen Kreis durchgeführt wird. Zuletzt verdoppelt man den Abstand des Bildpunktes doppelt so oft wie man den Radius halbiert hat. (Auch dies ist mit Zirkel allein möglich.) Dieser Punkt ist der gesuchte Bildpunkt.
- Auf Grund der Komplexität dieses Verfahrens wird man die Konstruktion wohl kaum durchführen, sie bietet aber eine Möglichkeit den Satz von Mohr-Mascheroni zu beweisen, der besagt, dass man mit Zirkel allein alle Konstruktionen durchführen kann, die mit Zirkel und Lineal möglich sind.
Mit anderen Hilfsmitteln
Es gibt mechanische Geräte, die speziell für die Inversion am Kreis konstruiert wurden, zum Beispiel den Inversor von Peaucellier.
Eigenschaften
- Die Abbildung vertauscht Inneres und Äußeres des Inversionskreises, die Punkte auf dem Rand sind Fixpunkte.
- Wendet man die Inversion zweimal an, so erhält man wieder die Ausgangssituation, die Inversion ist also eine Involution.
- Die Inversion ist eine konforme Abbildung, d.h., sie ist winkeltreu. Insbesondere werden Objekte, die einander berühren, auch wieder auf solche abgebildet.
- Die Inversion kehrt wie die Geradenspiegelung die Orientierung um.
- Geraden, die durch den Mittelpunkt des Inversionskreises verlaufen, werden auf sich selbst abgebildet.
- Geraden, die nicht durch den Mittelpunkt verlaufen, werden auf Kreise abgebildet, die durch den Mittelpunkt gehen.
- Kreise, die durch den Mittelpunkt verlaufen, werden auf Geraden abgebildet, die nicht durch den Mittelpunkt gehen.
- Kreise, die nicht durch den Mittelpunkt des Inversionskreises verlaufen, werden wieder auf solche Kreise abgebildet. Allerdings wird der Mittelpunkt des ursprünglichen Kreises durch die Inversion nicht auf den Mittelpunkt des Bildkreises abgebildet.
- Insbesondere werden Kreise, die den Inversionskreis rechtwinklig schneiden, auf sich selbst abgebildet.
Da die Inversion also nicht geradentreu ist, ist sie im Gegensatz zur Punkt-, Achsen- oder Ebenenspiegelung keine Kongruenzabbildung.
Literatur
- Coxeter, H. S. M., und S. L. Greitzer: Zeitlose Geometrie, Klett Stuttgart 1983


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.11. 2023