
Kongruenzabbildung
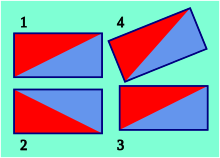
Achsenspiegelung (2)
Verschiebung (3)
Drehung (4)
Unter einer Kongruenzabbildung (von lateinisch congruens, deutsch‚ übereinstimmend, passend‘) versteht man in der Elementargeometrie, der synthetischen Geometrie und auch in der absoluten Geometrie eine geometrische Abbildung, bei der Form und Größe von beliebigen geometrischen Figuren nicht verändert werden, das heißt jede Figur wird dabei auf eine zu ihr kongruente abgebildet. Insbesondere lassen Kongruenzabbildungen den Abstand zwischen zwei beliebigen Punkten unverändert (invariant). Die Begriffe „Kongruenzabbildung“ und „Bewegung“ sind für die euklidische Geometrie gleichbedeutend, wobei meistens nur ebene Bewegungen als „Kongruenzabbildung“ bezeichnet werden. Auf die allgemeinere Bedeutung des Begriffs in der absoluten Geometrie wird im Abschnitt Synthetische und absolute Geometrie in diesem Artikel hingewiesen.
Darstellung und Eigenschaften
Kongruenzabbildungen in der Zeichenebene, also in der euklidischen Ebene, sind bijektive Abbildungen dieser Zeichenebene auf sich, die sich stets durch Hintereinanderausführung (Verkettung, Komposition) von Achsenspiegelungen zusammensetzen lassen.
Man unterscheidet eigentliche und uneigentliche Kongruenzabbildungen. Die eigentlichen Kongruenzabbildungen sind dadurch ausgezeichnet, dass sie durch Verkettung einer geraden Anzahl von Achsenspiegelungen darstellbar sind, während bei den uneigentlichen Kongruenzabbildungen dafür eine ungerade Anzahl benötigt wird. Es ist bewiesen, dass dabei eine Darstellung mit höchstens drei verketteten Achsenspiegelungen immer möglich ist. Besitzt eine Kongruenzabbildung einen Fixpunkt, so ist sie schon durch Verkettung (höchstens) zweier Achsenspiegelungen darstellbar.
Kongruenzabbildungen sind geraden-, längen- und winkeltreu. Sie bilden also Geraden auf Geraden ab und lassen Streckenlängen und Winkelgrößen unverändert. Sie sind auch bijektiv, das heißt umkehrbar, und ihre Umkehrabbildungen sind immer auch Kongruenzabbildungen.
Die Menge der ebenen Kongruenzabbildungen besteht aus
- Spiegelungen, genauer den Punkt- und den senkrechten Achsenspiegelungen, nicht jedoch Kreisspiegelungen und Schrägspiegelungen,
- Drehungen,
- (Parallel-)Verschiebungen (Translationen) und
- Gleit-/Schubspiegelungen.
Algebraisch gesehen bilden die Kongruenzabbildungen der Zeichenebene eine Gruppe. Kongruenzabbildungen sind spezielle Ähnlichkeitsabbildungen, noch allgemeiner gehören sie zu den Affinitäten.
In der analytischen Geometrie werden Kongruenzabbildungen mit Hilfe orthogonaler Matrizen beschrieben.
Geometrische Konstruktion in der Zeichenebene
Der allgemeine Fall
Zu zwei gegebenen, kongruenten Dreiecken
und
(bei der Kongruenz ist der Punkt
dem Punkt
zugeordnet usw.) lässt sich stets eine eindeutig bestimmte Kongruenzabbildung
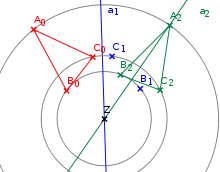
konstruieren. Vergleiche die Abbildung rechts: Gegeben sind die beiden Dreiecke,
deren Eckpunkte durch rote bzw. grüne Strecken verbunden sind.
- Konstruiere die Mittelsenkrechte
der Strecke
.
- Konstruiere die Spiegelpunkte von
und
(
bzw.
) bei der Spiegelung
an der Achse
. In dem Sonderfall, dass
ist, entfallen die ersten beiden Schritte, dann setzt man
und
.
- Konstruiere die Mittelsenkrechte
der Strecke
. Da das Dreieck
nach Konstruktion kongruent zu
und nach Voraussetzung zu
ist, sind die Strecken
und
gleich lang, das Dreieck
somit gleichschenklig und
geht auch durch
.
- Konstruiere den Spiegelpunkt
von
bei der Spiegelung
an
. In dem Sonderfall, dass
ist, entfällt der 3. und 4. Schritt und man setzt
.
- Nun können zwei Fälle auftreten: Entweder es gilt bereits
, wie in dem abgebildeten Beispiel, dann ist die Kongruenzabbildung durch die Komposition der genannten Achsenspiegelungen darstellbar oder man muss noch eine Spiegelung an der Verbindungsgeraden
durchführen die dann nach Voraussetzung
auf
spiegelt. (Hier wird der Kongruenzsatz SSS in der Form verwendet: Sind zwei verschiedene Punkte
und
der Ebene vorgegeben, dann gibt es höchstens zwei Punkte
, so dass die Streckenlängen
und
mit fest vorgegebenen Zahlen
erfüllen. Gibt es zwei Punkte
mit diesen Eigenschaften, dann geht das Dreieck
durch die Achsenspiegelung an der Verbindungsgeraden
in das Dreieck
über.)
Abgesehen von den beiden in 2. und 4. genannten Sonderfällen, also in den
Fällen, in denen
zwei verschiedene Achsenspiegelungen sind, ist die folgende Fallunterscheidung
interessant:
- Schneiden sich die beiden Achsen der Spiegelungen in einem Punkt
, dann ist die Abbildung
eine Drehung um
und der Drehwinkel der Drehung ist doppelt so groß wie ein orientierter Winkel
zwischen den beiden Achsen. Ein orientierter Winkel
ist dabei Drehwinkel einer der beiden Drehungen um
, die
auf
abbilden, welche der Drehungen man wählt ist gleichgültig.
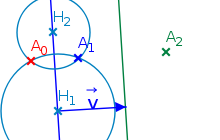
- Sind die beiden Achsen parallel, dann ist die Abbildung
eine Verschiebung um einen Verschiebungsvektor, dessen Länge das Doppelte des Abstands der beiden Achsen beträgt und hat dieselbe Richtung wie die zu den Achsen senkrechte Verschiebung
, die
auf
verschiebt, vergleiche die Abbildung rechts: Es gilt offenbar
.
Außerdem ergibt sich aus dem Konstruktionstext, dass die Kongruenzabbildung zwischen zwei ebenen, kongruenten Figuren durch drei Punkt-Bildpunktpaare eindeutig festgelegt ist, sofern die drei gewählten Urbildpunkte nicht auf einer gemeinsamen Gerade liegen. Mit anderen Worten: Die Gruppe der Kongruenzabbildungen operiert scharf einfach transitiv auf jeder Kongruenzklasse von Dreiecken (aufgefasst als geordnete Punkttripel). Das ist der inhaltliche Grund dafür, dass in der Elementargeometrie die Kongruenzsätze für Dreiecke eine überragende Rolle spielen.
Gleitspiegelung und Spiegelung
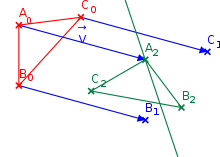
Zwei gegebene, gegensinnig kongruente Dreiecke
und
(bei der Kongruenz ist der Punkt
dem Punkt
zugeordnet usw.) können stets durch eine Gleitspiegelung
aufeinander abgebildet werden, vergleiche die Abbildung rechts:
- Verschiebe das Dreieck
(rot) mit der durch
definierten Verschiebung auf das (gleichsinnig kongruente) Dreieck
. Im Sonderfall
ist diese Verschiebung die identische Abbildung.
- Konstruiere die Mittelsenkrechte der Strecke
(grün). Wie beim 3. Schritt der allgemeinen Konstruktion sieht man, dass diese Mittelsenkrechte auch durch
gehen muss.
- Spiegele das Dreieck
an der Mittelsenkrechten aus dem 2. Schritt, das ergibt ein Dreieck
. Aus dem Kongruenzsatz SSS (siehe oben beim 5. Schritt der allgemeinen Konstruktion) und der Voraussetzung, dass die vorgegebenen Dreiecke gegensinnig kongruent sind, folgt
. In dem Sonderfall, dass
ist, entfällt der 2. Schritt und im 3. Schritt wird an der Verbindungsgeraden
gespiegelt. Dass damit
auf
abgebildet wird, folgt in diesem Sonderfall aus den gleichen Gründen wie bei der Spiegelung an der Mittelsenkrechten im allgemeinen Fall.
Aus diesem Konstruktionstext folgt:
- Zwei gegensinnig kongruente Dreiecke lassen sich stets durch eine Gleitspiegelung aufeinander abbilden.
-
- Die Verschiebung dabei sicher dann die identische Abbildung, die Abbildung also eine reine Spiegelung, wenn mindestens ein Paar von zugeordneten Eckpunkten bei der Kongruenz einen Punkt der Ebene sich selbst zuordnet.
- Genau dann, wenn eine der Strecken zwischen zugeordneten Punkten
,
,
die Länge 0 hat oder die Mittelsenkrechten aller drei Strecken zusammenfallen, ist die Gleitspiegelung eine reine Spiegelung.
- Sind zwei Dreiecke gegensinnig kongruent und stimmen sie in mindestens einem Eckpunkt, der sich selbst zugeordnet ist, überein, dann stimmen sie in zwei solchen Eckpunkten überein oder die Mittelsenkrechten der anderen beiden Strecken zwischen zugeordneten Punkten fallen zusammen. Das ist eine Verallgemeinerung der oben genannten Formulierung des Kongruenzsatzes SSS.
Zusammen mit dem allgemeinen Konstruktionstext ergibt sich:
- Eine nichtidentische Drehung ist immer als Komposition von zwei verschiedenen Achsenspiegelungen darstellbar. Diese Achsenspiegelungen sind durch die Drehung im Allgemeinen nicht eindeutig bestimmt, ihre Achsen schneiden sich jedoch stets im Zentrum der Drehung und für den Winkel zwischen den Achsen gilt die oben beschriebene Beziehung zum Winkel der Drehung.
- Die Hintereinanderausführung einer Drehung und einer Achsenspiegelung in beliebiger Reihenfolge ist stets eine Gleitspiegelung.
Darüber hinaus gilt:
- Die Hintereinanderausführung einer Verschiebung und einer nichtidentischen Drehung in beliebiger Reihenfolge ist eine Drehung.
- Im Allgemeinen wird eine Gleitspiegelung – Verschieben um einen Vektor
und anschließend Spiegeln an einer Achse
– zu einer anderen Gleitspiegelung, wenn man die Reihenfolge der beiden Kongruenzabbildungen vertauscht.
Abgrenzung zu den Bewegungen
Vom Standpunkt der analytischen Geometrie besteht kein Unterschied zwischen den Begriffen Kongruenzabbildung und Bewegung. In der Elementargeometrie nennt man aber in der Regel nur eine Bewegung der euklidischen Ebene Kongruenzabbildung, also nur Bewegungen im zweidimensionalen Fall.
Schulmathematik
Die Schulmathematik geht zunächst von der Zeichenebene aus. Der Begriff „Kongruenz“ wird für einfache Figuren (Dreiecke, Vierecke, Kreise, …) erfahrbar gemacht:
- Man kann eine Figur, die idealerweise auf durchscheinendes Papier oder Folie gezeichnet ist, ausschneiden und so auf die andere Figur legen, dass beide „zur Deckung kommen“, also sind die beiden Figuren „deckungsgleich“.
- Man kann zwei deckungsgleiche Figuren mit ein und derselben „Schablone“ zeichnen.
Darauf aufbauend wird später die Erfahrung gemacht, dass man „manchmal“ die Kongruenz von Figuren ohne Ausschneiden zeichnerisch einsehen kann.
- Manchmal kann man zwei Figuren, die auf dem gleichen durchscheinenden Blatt gezeichnet sind, ohne Ausschneiden durch Falten des Papiers zur Deckung bringen. Das Falten kann man dann zur Konstruktion einer Achsenspiegelung abstrahieren.
- Anstatt eine Figur wirklich auszuschneiden und „unverdreht“ zu verschieben, kann man die Verschiebung durch parallele und gleich lange Pfeile an den Eckpunkten einer Figur abstrakt darstellen.
- Ähnlich kann man auch eine wirkliche, physische Drehung einer ausgeschnittenen Figur, die an einem inneren Punkt mit einer Nadel festgepinnt ist, abstrakt zeichnerisch mit den Bewegungskreisen der Eckpunkte darstellen.
Die Tatsache, dass man mit diesen drei zeichnerischen Abstraktionen und ihren Kombinationen alle „experimentellen“ Kongruenzbeweise durch Ausschneiden und Übereinanderlegen ersetzen kann, sollte intuitiv erfasst werden. (Mathematisch ausgedrückt: Dass die Gruppe der Kongruenzabbildungen durch Achsenspiegelungen, Verschiebungen und Drehungen erzeugt wird.) Bewiesen wird dagegen, dass man jede Verschiebung und jede Drehung durch zwei geeignete Achsenspiegelungen ersetzen kann.
Ein Beispiel für die Probleme, die in der Schulmathematik auftreten, ist die Abgrenzung zwischen „Gleichheit“ von geometrischen Objekten und „Kongruenz“: Intuitiv und umgangssprachlich werden zwei gleich lange, also kongruente Strecken als „gleich“ angesehen und bezeichnet. Die Schülervorstellung, dass jedenfalls zwischen gleichsinniger Deckungsgleichheit und Identität von Figuren nicht unterschieden werden müsste, stellt ein didaktisches Problem dar.
Einigen Problemen kann dadurch begegnet werden, dass exemplarisch „echte Deduktionen“, also Beweise wirklich erarbeitet werden, bei denen die kongruenten Figuren aufgrund der Problemstellung nicht identisch sein können bzw. bei denen es auf die Reihenfolge der zugeordneten Punkte bei der Kongruenz ankommt.
Synthetische und absolute Geometrie
Beim axiomatischen Aufbau einer euklidischen Ebene in der synthetischen Geometrie und beim Aufbau der absoluten Geometrie gehören die Begriffe „Kongruenzabbildung“ und „ebene Bewegung“ zu unterschiedlichen deduktiven Ansätzen:
- Von der Kongruenz zur Kongruenzabbildung: Man beschreibt die Kongruenz als Grundbegriff axiomatisch. In Hilberts Axiomensystem der euklidischen Geometrie wird diese durch zwei Äquivalenzrelationen auf der Menge der Strecken und der Winkel der Ebene realisiert (Gruppe III, Axiome der Kongruenz). Dann ist eine Kongruenzabbildung eine bijektive Selbstabbildung der Ebene, bei der jede Kongruenzklasse auf sich abgebildet wird.
- Vom Spiegelungsbegriff oder der Bewegungsgruppe zur Kongruenz: Man stattet die Ebene mit einer axiomatisch definierten Orthogonalitätsrelation aus. Das ermöglicht dann die Definition von senkrechten Achsenspiegelungen, siehe dazu präeuklidische Ebene. Eine Bewegung der Ebene ist dann jede Abbildung, die sich als Komposition von endlich vielen solchen Achsenspiegelungen darstellen lässt. Ein anderer verwandter Ansatz, der auch in der absoluten Geometrie verwendet wird, fasst die Eigenschaften der Bewegungsgruppe selbst axiomatisch. Bei beiden Ansätzen ist die Bewegungsgruppe grundlegend und Kongruenz ein daraus abgeleiteter Begriff. Zwei Figuren sind kongruent, wenn sie zur gleichen Bahn der Gruppenoperation gehören, bei der die Bewegungsgruppe auf der Menge aller Teilmengen der Ebene (Potenzmenge) operiert.
Die Schulgeometrie in Deutschland orientiert sich in aller Regel an einem deduktiven Ansatz nach Hilbert, bei dem die Kongruenz ein Grundbegriff ist. Man spricht dann in der Ebene überhaupt nur von Kongruenzabbildungen und der Begriff Bewegung tritt, wenn überhaupt, erst in der dreidimensionalen Geometrie auf.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.02. 2021