
Affinität (Mathematik)
In der Geometrie bezeichnet man als Affinität eine strukturerhaltende bijektive Abbildung eines affinen Raumes (häufig der Zeichenebene oder des dreidimensionalen Anschauungsraums) auf sich selbst. Der Begriff umfasst und verallgemeinert den Begriff der Ähnlichkeit, bei der zusätzlich die Verhältnisse beliebiger Streckenlängen und die Maße von Winkeln (→ siehe Winkeltreue) erhalten bleiben.
- Eine Affinität ist also eine affine Abbildung eines affinen Raumes in sich selbst, welche zugleich eine Bijektion ist. Sie hat damit stets die Eigenschaft, dass
- die Punkte und Geraden des Raumes auf Punkte bzw. Geraden unter Erhaltung der Kollinearität abgebildet werden: Punkte auf einer Geraden werden auf Punkte der zugehörigen Bildgeraden abgebildet,
- das Teilverhältnis von beliebigen drei Punkten auf einer beliebigen Geraden erhalten bleibt (Teilverhältnistreue) und
- jedes Paar paralleler Geraden auf ein Paar paralleler Geraden abgebildet wird (Parallelentreue).[1]
- Jede Affinität ist eine Kollineation, hat also die erstgenannte Eigenschaft der Geradentreue.
- Im Euklidischen Raum verändert eine Affinität im Allgemeinen die Längen von Strecken und die Maße von Winkeln und damit auch Flächen- und Rauminhalte. Affinitäten des Euklidischen Raumes, welche auch diese Größen unverändert lassen, also Isometrien sind, heißen Bewegungen.
- Ebenso werden durch eine Affinität eines Euklidischen Raumes im Allgemeinen die Verhältnisse von Strecken (Längenverhältnisse) verändert. Werden sie und damit auch Winkel zwischen Geraden dagegen nicht verändert, so nennt man eine solche Affinität Ähnlichkeit.
In der synthetischen Geometrie wird der Begriff Affinität für zweidimensionale affine Räume, also Ebenen verallgemeinert: Eine Kollineation auf einer affinen Ebene ist genau dann eine Affinität, wenn jede ihrer Einschränkungen auf eine Gerade durch eine Komposition von Parallelprojektionen dargestellt werden kann. Für desarguesche Ebenen ist diese Definition äquivalent zu der Definition „Eine Affinität ist eine teilverhältnistreue Kollineation.“, die in der analytischen Geometrie verwendet wird. Für mindestens dreidimensionale affine Räume erübrigt sich eine Verallgemeinerung, da diese stets desarguesch sind, eindimensionale Räume werden für sich genommen in der synthetischen Geometrie nicht betrachtet.
Koordinatendarstellung
Man kann die Abbildungsvorschrift nach Wahl einer affinen Punktbasis
für die Ortsvektoren
in der Form
angeben. Der Vektor
heißt Verschiebungsvektor,
ist eine quadratische
Matrix,
die sogenannte Abbildungsmatrix.
Für ihre Determinante
ist stets
,
d.h. die Abbildung ist bijektiv.
Hier wird der affine Raum als ein Vektorraum
über einem Körper
(in der Geometrie meist
)
aufgefasst. Die Punkte des affinen Raumes sind die Vektoren aus
(Ortsvektoren), und affine Unterräume
sind die additiven Nebenklassen
der linearen Unterräume dieses Vektorraums
.
Von dem Vektorraum
wird dabei in der Geometrie stets und auch in der Linearen Algebra überwiegend
vorausgesetzt, dass seine Dimension
endlich ist.
Klassifizierung von Affinitäten
Radiale Affinitäten
Eine Affinität heißt radiale/zentrische Affinität, wenn sie genau
einen Fixpunkt
besitzt, dies ist äquivalent zu .
- (Der Rang
wird in Rang erläutert.)
Perspektive Affinitäten
Eine Affinität heißt perspektive Affinität, wenn sie genau eine
Fixpunkthyperebene (das heißt eine
ausschließlich aus Fixpunkten bestehende Hyperebene) besitzt, was äquivalent zu
ist.
Eine perspektive Affinität heißt Parallelstreckung, wenn sie neben dem
Eigenwert
(das heißt einem Eigenwert von
)
noch einen Eigenwert
besitzt.
Eine Parallelstreckung mit
heißt Affinspiegelung. Sie heißt Scherung,
wenn sie nur den Eigenwert
besitzt.
Eine perspektive Affinität besitzt ein Invariantes Rechtwinkelpaar.
Homothetien
Eine Affinität mit
mit
heißt Homothetie oder Dilatation.
Falls außerdem
, heißt
Zentralstreckung.
, heißt
Verschiebung oder Translation
, heißt
Punktspiegelung.
Unimodularität
Eine Affinität heißt unimodular, wenn .
Sie ist eigentlich unimodular, wenn .
Inhaltstreue
Ist der zugrunde liegende Körper angeordnet, so ist eine Affinität
inhaltstreu, wenn .
Sie ist gleichsinnig, wenn .
Eigenschaften allgemeiner Affinitäten
Affinitäten besitzen eine Reihe von Eigenschaften, die bei Konstruktionen ausgenutzt werden können.
Bijektivität
Eine Affinität ist sowohl injektiv als auch surjektiv, also bijektiv.
Geradentreue
Das Bild einer Geraden unter einer Affinität ist wieder eine Gerade.
Parallelentreue
Die Bilder paralleler Geraden unter einer Affinität sind wieder parallel.[1]
Teilverhältnistreue
Ist
ein Punkt der Strecke
und sind
die Bilder von
und
unter einer Affinität, so ist das Teilverhältnis
von
gleich dem Teilverhältnis von
.
Speziell gilt: Ist
Mittelpunkt von
,
so ist der Bildpunkt von M unter einer Affinität der Mittelpunkt der Strecke
.
Eigenschaften ebener perspektiver Affinitäten
Bei einer perspektiven Affinität in einem zweidimensionalen affinen Raum, der Ebene, ist die Fixpunkthyperebene eine Gerade, die auch als Achse der Affinität bezeichnet wird. Man spricht hier auch von Achsenaffinitäten.
Geraden durch Punkt und Bildpunkt sind Fixgeraden
Eine Gerade ,
durch einen Punkt
und seinen Bildpunkt
ist eine Fixgerade. Dies lässt sich
mit Hilfe der Fixpunktgerade
der perspektiven Affinität zeigen:
- Wenn
die Fixpunktgerade
in einem Punkt
schneidet, so ist das Bild von
aufgrund der Geradentreue die Gerade
. Diese fällt aber mit
zusammen.
- Wenn
parallel zu
ist, dann ist das Bild von
aufgrund der Parallelentreue eine Parallele zu
durch
, da das Bild von
gleich
selbst ist. Diese Parallele fällt aber mit
zusammen.
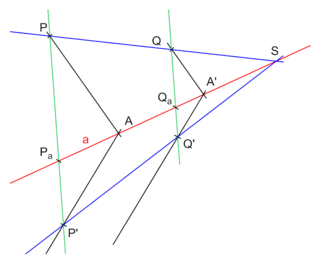
Parallelen von Fixgeraden sind wieder Fixgeraden
Das Bild
zu einer Fixgeraden
ist selbst wieder eine Fixgerade. Die Aussage folgt aus der Parallelen- und
Teilverhältnistreue:
- Da
und
parallel sind, muss auch
und
parallel sein. Aus der Transitivität der Parallelität folgt, dass dann auch
und
parallel sein müssen.
- Wähle einen Punkt
auf der Affinitätsachse
und einen Punkt
auf
.
- Da
und
parallel sind, schneidet die Verbindungsgerade
auch
in einem Punkt
.
- Da
eine Fixgerade ist, liegt das Bild
von
auf
und das Bild von
ist gleich
.
- Über die Verhältnistreue folgt, dass
zu
wie
zu
.
- Mit der Umkehrung des ersten Strahlensatzes
ergibt sich, dass dann
auf einer Parallele zu
durch
(also auf
) liegen muss. Da
und
parallel sind und den Punkt
gemeinsam haben, müssen sie identisch sein.
Konstruktionen
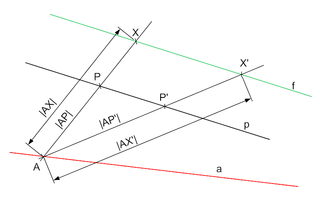
Bildpunkt unter einer perspektiven Affinität
Gegeben sei eine perspektive Affinität über ihre Fixpunktgerade
und das Punkt/Bildpunkt-Paar
,
.
Das Bild eines beliebigen Punktes
lässt sich damit wie folgt konstruieren:
- Wähle einen beliebigen Punkt
auf der Fixpunktgeraden
.
- Zeichne die Verbindungsgerade
.
- Das Bild von
ist aufgrund der Geradentreue der Abbildung wieder eine Gerade. Das Bild von
ist
selbst, da
auf der Fixgeraden
liegt. Damit ist das Bild von
die Gerade
.
- Zeichne eine Parallele zu
durch
. Diese schneidet
in einem Punkt
. Aufgrund der Parallelentreue der Abbildung ist das Bild von
eine Parallele zu
durch den Punkt
. Der gesuchte Punkt
liegt auf dieser Parallelgeraden.
- Zeichne die Gerade
. Sie schneidet
in einem Punkt
(ist das nicht der Fall, ist eine Sonderbehandlung notwendig). Das Bild dieser Geraden ist
. Der gesuchte Punkt
liegt ebenfalls auf dieser Geraden und ist daher der Schnittpunkt von
und der Parallele von
durch
.
Eine andere Möglichkeit der Konstruktion spart den Hilfspunkt
ein und nutzt die Eigenschaft aus, dass Geraden durch Punkt und Bildpunkt Fixgeraden
sind:
- Zeichne die Gerade
. Da es sich um eine Gerade durch Punkt und Bildpunkt handelt, ist das Bild dieser Geraden die Gerade selbst.
- Zeichne eine Parallele
zu
durch
. Sie schneidet die Fixgerade
in
.
- Das Bild von
ist
selbst:
- Geradentreue: Da
parallel zu
, verläuft das Bild von
parallel zum Bild von
.
ist eine Fixgerade: Das Bild von
ist
selbst. Daraus folgt, dass das Bild von
parallel zu sich selbst ist.
- Da der Punkt
Teil der Fixpunktgeraden
ist, ist das Bild von
gleich
selbst.
- Da das Bild von
durch
verläuft und parallel zu sich selbst ist, kann es nur
selbst sein.
- Geradentreue: Da
- Damit ist
Teil von
.
- Mit der Überlegung der ersten Konstruktion liegt damit
auf dem Schnittpunkt von
und
(mit dem Schnittpunkt
von
und
).
Gruppenstruktur
Die Menge der Affinitäten über einem affinen Raum
bilden bezüglich der Hintereinanderausführung
eine Gruppe.
Ist dem affinen Raum
der
-dimensionale
Vektorraum
zugeordnet, dann lässt sich diese Gruppe (hier abkürzend als
geschrieben) in die Allgemeinen
linearen Gruppen als Untergruppe einordnen.
Die Gruppe der Affinitäten ist auch eine Untergruppe der Gruppe der (ebenentreuen) Kollineationen.
Gruppenoperationen
Durch die von einer Affinität geforderten Eigenschaften ergeben sich in natürlicher Weise verschiedene Gruppenoperationen:
operiert als Abbildungsgruppe
-
- auf der Punktmenge
,
- auf der Menge der affinen Teilräume von
einer festen Dimension
mit
,
- auf Mengen von Richtungen im affinen Raum, zum Beispiel der Menge aller Scharen paralleler Geraden.
- auf der Punktmenge
- Die Gruppe
operiert scharf einfach transitiv auf der Menge der affinen Punktbasen des affinen Raums
. Das bedeutet hier: Gibt man
Punkte in allgemeiner Lage (so, dass die Verbindungsvektoren des ersten Punktes mit den übrigen
Punkten linear unabhängig sind) vor, dann gibt es genau eine Affinität, bei der die Standardbasis auf diese Punkte (in der vorgegebenen Reihenfolge) abgebildet wird. Daraus ergibt sich eine einfache Möglichkeit, die Anzahl der Elemente von
zu berechnen, wenn
ein endlicher Körper ist.
Gruppenstruktur
Die Gruppe
- ist für
stets nichtkommutativ,
- enthält die allgemeine lineare Gruppe
als Untergruppe – die Affinitäten, bei denen der fest gewählte Ursprung
Fixpunkt ist, deren Translationsanteil oder Verschiebungsvektor also der Nullvektor ist,
- kann als Untergruppe der allgemeinen linearen Gruppe
aufgefasst werden,
- kann als Untergruppe der Projektiven
linearen Gruppe
aufgefasst werden – hier gehören jene Projektivitäten zu
, die eine feste Hyperebene des projektiven Raumes, die Fernhyperebene als Fixhyperebene auf sich selbst abbilden,
- enthält die kommutative Untergruppe der Translationen (reine
Verschiebungen, deren Abbildungsmatrix
die Einheitsmatrix ist)
als Normalteiler,
- ist inneres semidirektes
Produkt von
und
.
- Der Normalteiler
der Translationen ist isomorph zur additiven Gruppe
des zugrundeliegenden Vektorraums.
operiert durch Konjugation scharf einfach transitiv auf der Menge von Untergruppen
. Dabei ist
diejenige Untergruppe von
, die einen bestimmten Punkt
des affinen Raumes auf sich abbildet. Jede dieser Untergruppen ist zu
isomorph.
Gruppenordnung
Ist der Körper
ein endlicher
Körper mit
Elementen, dann ist die Gruppe der Affinitäten
endlich und ihre Ordnung
ist
-
.
Dabei ist der Faktor
die Ordnung der Translationsgruppe
,
er ist zugleich der Index
der Untergruppe
,
die den Ursprung auf sich abbildet. Die Ordnung dieser Untergruppe liefert die
übrigen Faktoren (→siehe Allgemeine
lineare Gruppe#Über endlichen Körpern).
Literatur
- Gerd Fischer: Analytische Geometrie. 6., überarbeitete Auflage. Vieweg Verlag, Braunschweig [u.a.] 1992, ISBN 3-528-57235-3.
- Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik, Band II: Lineare Algebra. BI-Wissenschafts-Verlag, 1990, ISBN 3-411-14101-8.
- Günter Scheja, Uwe Storch: Lehrbuch der Algebra: unter Einschluß der linearen Algebra. 2., überarb. und erw. Auflage. Teubner, Stuttgart 1994, ISBN 3-519-12203-0.
Anmerkungen
- ↑ a b Die Parallelentreue folgt aus der ersten Forderung an eine Affinität, der Erhaltung der Kollinearität, außer im Falle von affinen Räumen mit genau zwei Punkten auf jeder Geraden, die mindestens dreidimensional sind. In allen Fällen ist sie, wenn die Geradentreue vorausgesetzt wird, äquivalent zur Ebenentreue (Scheja und Storch §43 und V.I). Vergleiche hierzu auch die ausführlichen Erläuterungen in Kollineation.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.12. 2021