Streckensymmetrale

Die Mittelsenkrechte oder das Mittellot oder (österreichisch) Streckensymmetrale ist eine besondere Gerade, die in der ebenen Geometrie untersucht wird. Eine Verallgemeinerung auf drei Dimensionen ist die Mittellotebene.

Definition

Die Streckensymmetrale ist die Menge aller Punkte, die von zwei gegebenen Punkten denselben Abstand haben:

$s = \left\{X\mid\overline{XA} = \overline{XB}\right\}$

Eine andere Definitionsmöglichkeit lautet: Die Streckensymmetrale ist die Menge der Mittelpunkte aller Kreise, die durch zwei gegebene Punkte gehen.

Die Streckensymmetrale ist also eine Gerade, die orthogonal (das heißt senkrecht) auf der Verbindungsstrecke der zwei Punkte steht und durch deren Mittelpunkt geht.

Konstruktion

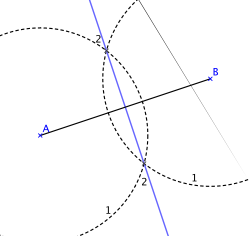
Konstruktion einer Streckensymmetrale

Man konstruiert eine Mittelsenkrechte zwischen zwei gegebenen Punkten und , indem man um diese beiden Punkte mit einem Zirkel Kreisbögen zeichnet mit gleichem Radius, der größer als die halbe Strecke zwischen den beiden Punkten sein muss. Die zwei Schnittpunkte dieser beiden Kreislinien bestimmen eine Gerade. Diese Gerade ist die Mittelsenkrechte der Strecke .

Berechnung im Koordinatensystem

Sind in einem zweidimensionalen kartesischen Koordinatensystem zwei Punkte A(x_A|y_A) und B(x_B|y_B) mit $y_A\ne y_B$ gegeben, so lautet die Geradengleichung der Mittelsenkrechte:

$y=-\frac{x_A-x_B}{y_A-y_B}x+\frac{x_A^2-x_B^2+y_A^2-y_B^2}{2 \cdot(y_A-y_B)}$

Ist y_A = y_B , so lautet die (Nicht-Funktions-)Gleichung: $x= \frac 1 2 (x_A+x_B)$

Mittelsenkrechten im Dreieck

Die Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt, nämlich im Umkreismittelpunkt des Dreiecks. Dieser Umkreis geht durch alle Ecken des Dreiecks (siehe dazu auch: Ausgezeichnete Punkte im Dreieck).

Mittellotebene

Die Mittellotebene zu zwei Punkten und im Raum ist die Ebene, die zur Verbindungsstrecke [AB] senkrecht ist und durch den Mittelpunkt dieser Strecke geht, also die Symmetrieebene der Punkte und .

In der analytischen Geometrie erhält man eine Gleichung der Mittellotebene in Normalenform dadurch, dass man den Vektor $\vec{n} = \vec{AB}$ als Normalenvektor und den Punkt (mit dem Ortsvektor $\vec{m}$ ) als Aufpunkt verwendet:

$\vec{n} \cdot \left( \vec{x} - \vec{m} \right) = 0$

Siehe auch

Umkreis

Basierend auf einem Artikel in:

Wikipedia.de