Euklidischer Körper

Ein euklidischer Körper ist ein Körper (im Sinne der Algebra), der ein geordneter Körper ist und in dem jedes nichtnegative Element eine Quadratwurzel hat.

Jeder reell abgeschlossene Körper ist euklidisch und jeder euklidische Körper ist ein pythagoreischer und formal reeller Körper.

Euklidische Körper spielen in der synthetischen Geometrie eine wichtige Rolle: Der Koordinatenkörper einer euklidischen Ebene $K^{2}$ ist stets ein euklidischer Körper, auf diesen Körpern lässt sich stets eine euklidische Ebene aufbauen. Der Begriff „Euklidische Ebene“ ist dabei etwas allgemeiner als in der üblichen Geometrie, wo die euklidische Ebene etwa durch Hilberts Axiomensystem der euklidischen Geometrie so definiert wird, dass sie zwingend eine affine Ebene über dem speziellen euklidischen Körper der reellen Zahlen ist – eine zu Hilberts System gleichwertige Formulierung in der Sprache der linearen Algebra lautet: Eine euklidische Ebene ist ein affiner Raum, dessen Vektorraum der Verschiebungen ein zweidimensionaler euklidischer Vektorraum, also isomorph zu $(\R^2, \langle \cdot, \cdot \rangle)$ mit einem Skalarprodukt ist. Die euklidischen Ebenen der synthetischen Geometrie stehen in engem Zusammenhang mit klassischen Fragen der Konstruierbarkeit. Aus diesen Fragestellungen ergeben sich zusätzliche Axiome, wie das Winkelmesseraxiom, das die Existenz eines Bogenmaßes fordert, und das Winkelteilungsaxiom, die nicht in allen euklidischen Ebenen erfüllbar sind.

Ersetzt man in der analytisch formulierten zwei- oder dreidimensionalen, reellen euklidischen Geometrie die reellen Zahlen als Koordinatenbereich durch einen beliebigen archimedischen euklidischen Körper, dann kann man innerhalb dieser Geometrie Modelle für nichteuklidische Geometrien konstruieren, die anstelle der Axiome der Stetigkeit (Axiomengruppe V in Hilberts Axiomensystem) die etwas schwächeren Axiome des Zirkels erfüllen. In diesen Modellen der absoluten Geometrie sind dann immer noch alle Konstruktionen mit Zirkel und Lineal ausführbar.

Eine gewisse Bedeutung haben euklidische Körper als Gegenbeispiele in der Theorie der Körpererweiterungen und der Galoistheorie, daneben bei Transzendenzuntersuchungen in der Zahlentheorie.

Euklidische Körper und Ebenen tragen ihre Namen zu Ehren des antiken Mathematikers Euklid von Alexandria, wobei beide ihren Namen seinem axiomatischen Aufbau der – bis heute nach ihm benannten – euklidischen Geometrie in seinem Werk „Die Elemente“ verdanken. → Der Begriff „Euklidischer Ring“ aus der Teilbarkeitstheorie in kommutativen Ringen steht in keinem engeren inhaltlichen Zusammenhang zu den im vorliegenden Artikel beschriebenen Begriffen als dem, dass er ebenfalls nach Euklid und zwar nach dem von ihm beschriebenen euklidischen Algorithmus benannt ist.

Alternative Definitionen

Ein pythagoreischer Körper , also ein Körper, in dem jede Summe von Quadraten wieder ein Quadrat ist, ist genau dann ein euklidischer Körper, wenn er genau die zwei Quadratklassen Q_1 und $Q_{-1}$ enthält. Zwar ist durch diese rein algebraische Definition noch keine Anordnung gegeben, aber es gibt in solchen pythagoreischen Körpern nur genau eine Möglichkeit, sie zu einem geordneten Körper zu machen und zwar durch die Definition

genau dann, wenn b-a

ein Quadrat (also ein Element von Q_1 ) ist.

Damit kann man diese „kanonische Anordnung“ als durch die algebraische Struktur gegeben ansehen. In den folgenden Definitionen sollen alle Körper, die nur eine Anordnung zulassen, die dann immer diese kanonische ist, als so angeordnet angesehen werden.

Ein Körper ist genau dann euklidisch, wenn er

ein geordneter pythagoreischer Körper mit genau zwei Quadratklassen,
ein pythagoreischer Körper mit genau zwei Quadratklassen und $Q_{-1}$ ,
ein formal reeller Körper mit genau zwei Quadratklassen,
ein Körper der Charakteristik 0 mit genau zwei Quadratklassen und $Q_{-1}$
ein formal reeller Körper, der keine formal reelle, quadratische Körpererweiterung zulässt oder
geordnet, $K^+=(K\setminus\{0\})^2$ seine Ordnung (Menge seiner positiven Zahlen), eine Untergruppe vom Index 2 in seiner multiplikativen Gruppe und seine Charakteristik 0

ist.

Eigenschaften

Ein euklidischer Körper

hat stets die Charakteristik 0,
enthält immer unendlich viele Elemente,
ist nie algebraisch abgeschlossen,
ist stets formal reell und pythagoreisch,
enthält zu jeder reinquadratischen Gleichung $X^2-c=0\!\,\ (c\in K, c>0)$ genau zwei verschiedene Lösungen,
kann auf genau eine Art angeordnet werden,
ist genau dann reell abgeschlossen, wenn algebraisch abgeschlossen ist,
besitzt als einzigen Körperautomorphismus die identische Abbildung (ist ein starrer Körper).

Eine Verschärfung der letztgenannten Eigenschaft: Ist K<L eine Körpererweiterung und ist ein euklidischer und ein formal reeller Körper, dann gibt es genau eine Einbettungsabbildung von nach .

Und eine Folgerung der letztgenannten Eigenschaft: Eine Körpererweiterung K<L mit einem euklidischen Erweiterungskörper ist genau dann galoissch über , wenn K=L ist.

In geometrischen Anwendungen sind euklidische Körper meist Teilkörper der reellen Zahlen und also archimedisch angeordnet. Dass dies nicht notwendig so sein muss, zeigt das Beispiel der hyperreellen Zahlen.

Beispiele und Gegenbeispiele

Das Hauptbeispiel eines euklidischen Körpers bildet $\mathbb {R}$ , der Körper der reellen Zahlen.

Daneben gelten als wichtige Beispiele:

die reellen algebraischen Zahlen $\mathbb A \cap \R$ (das sind die reellen Zahlen im algebraischen Abschluss $\mathbb A$ des Körpers der rationalen Zahlen $\mathbb {Q}$ ),
die hyperreellen Zahlen.

Für jede Teilmenge von $\mathbb {R}$ , die $\mathbb {Z}$ enthält, ist die Menge der aus „mit Zirkel und Lineal konstruierbaren“ reellen Zahlen ein euklidischer Körper. Dieser Körper ist der kleinste euklidische Körper, in dem als Teilmenge enthalten ist, und für $M=\Z$ der kleinste euklidische Körper überhaupt: Jeder euklidische Körper enthält einen zu isomorphen Teilkörper.

Der genannte kleinste euklidische Körper besteht genau aus denjenigen reellen algebraischen Zahlen , für die ein Turm von quadratischen Körpererweiterungen $\mathbb{Q}\!\, =K_0\subsetneq K_1 \subsetneq \ldots \subsetneq K_m$ existiert, so dass $c\in K_m$ und $K_{k+1}=K_k(\sqrt{\alpha_k})$ für ein $\alpha_k\in K_k$ ist. Notwendig für die Existenz des Turms ist dabei, dass der Erweiterungsgrad der Körpererweiterung $\Q(c)/\Q$ eine Potenz von 2 ist $\left(\left[ \Q(c):\Q\right]=2^r; r\in \N_0\right)$ .
Der euklidische Körper der aus einer Menge $\left(\Z \subseteq M\subseteq \R\right)$ mit Zirkel und Lineal konstruierbaren Zahlen besteht genau aus denjenigen reellen und über $\Q(M)$ algebraischen Zahlen , für die ein entsprechender Turm über $K_0=\Q(M)$ existiert, und der Grad von über $K_{0}$ ist dann notwendig eine Potenz von 2.

Dass die beschriebenen Mengen tatsächlich Körper sind, das heißt, dass mit 2 Elementen mit der angegebenen Eigenschaft auch deren Summe und Produkt etc. die geforderte Eigenschaft hat, ist am einfachsten geometrisch einzusehen. → Siehe konstruierbares Polygon.

In allen Fällen sind die euklidischen Körper über $\mathbb {Q}$ unendlichdimensionale $\mathbb {Q}$ -Vektorräume, das heißt Körpererweiterungen unendlichen Grades.

$\mathbb {Q}$ ist ein Beispiel für einen formal reellen Körper, der nicht euklidisch ist.
Der kleinste euklidische Körper ist euklidisch, aber nicht reell abgeschlossen, da die Nullstellen von im algebraischen Abschluss von $\mathbb {Q}$ alle den Grad 3 über $\mathbb {Q}$ haben und daher nicht in liegen, damit kann auch nicht algebraisch abgeschlossen sein.

Euklidische Ebenen und die euklidische Ebene

zum archimedischen Axiom

Euklidische Ebenen in der synthetischen Geometrie erfüllen alle Axiome der Axiomengruppen I bis IV in Hilberts Axiomensystem, aber nicht immer die beiden Stetigkeitsaxiome, die die Gruppe V bilden:

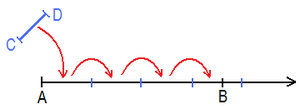
V.1. (Axiom des Messens oder Archimedisches Axiom). Sind AB und CD irgendwelche Strecken, so gibt es eine Anzahl n derart, dass das n-malige Hintereinanderabtragen der Strecke CD von A aus auf den durch B gehenden Halbstrahl über den Punkt B hinausführt.
V.2. (Axiom der (linearen) Vollständigkeit) Zu den Punkten einer Geraden können, bei Erhalt ihrer Anordnungs- und Kongruenzbeziehungen, keine weiteren Punkte hinzugefügt werden, ohne dass die unter den vorherigen Elementen bestehenden Beziehungen, die aus den Axiomen I-III folgenden Grundeigenschaften der linearen Anordnung und Kongruenz oder aber das Axiom V.1 verletzt werden.

In der Nonstandardmathematik (Internal Set Theory) kann das archimedische Axiom übertragen werden: Anstelle einer endlichen Anzahl $n\in \mathbb {N}$ von Abtragungen, wird dann in der Nonstandardversion die hyperendliche Anzahl in der inneren Menge $\N^*$ zugelassen. Für diese euklidischen Ebenen sind dann (bei entsprechender Übertragung aller anderen Axiome, die auf unendliche Teilmengen der Ebene oder endliche Zählmengen mit unbestimmter Anzahl Bezug nehmen) genau die reelle und die hyperreelle euklidische Ebene ein Modell. - In dieser hyperreellen euklidischen Ebene kann ein reguläres Vieleck auch eine wohlbestimmte hyperendliche Anzahl von Ecken haben. Die synthetische Standardgeometrie liefert auch über dem euklidischen Körper der hyperreellen Zahlen nicht diese Geometrie.

In der Standardgeometrie werden die Axiome der Stetigkeit durch Axiome des Zirkels ersetzt, die gewährleisten, dass die Konstruktionen mit Zirkel und Lineal niemals aus dem Koordinatenbereich herausführen. Dann erfüllen genau die Ebenen über euklidischen Körpern, wie sie in diesem Artikel beschrieben sind, das neue Axiomensystem.

zum euklidischen Anordnungsaxiom

Ein anderes Axiomensystem, das diese euklidischen Ebenen beschreibt, erhält man, wenn man zusätzlich zu den Axiomen einer pythagoreischen Ebene das folgende euklidische Anordnungsaxiom hinzunimmt:

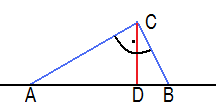
(E) Es gibt eine Anordnung „zwischen“, so dass von drei verschiedenen kollinearen Punkten, A,B,D

genau dann zwischen und liegt, wenn sich über der Strecke

ein bei rechtwinkliges Dreieck ABC

mit dem Höhenfußpunkt errichten lässt.

Die Anordnung „zwischen“ auf Geraden der Ebene muss natürlich die anderen, von den Anordnungen auf einer pythagoreischen Ebene geforderten geometrischen Eigenschaften erfüllen, woraus dann folgt, dass sie von einer der in formal reellen pythagoreischen Körpern stets möglichen Körperanordnungen induziert wird.

Eine affine Ebene ist genau dann euklidisch (im Sinne der synthetischen Geometrie), wenn sie eine pythagoreische Ebene ist und (E) erfüllt. Jede Koordinatenebene $K^{2}$ über einem euklidischen Körper wird durch die Anordnung, die von der in einzig möglichen Körperanordnung induziert wird, und durch die (bis auf Koordinatentransformation) einzig mögliche Orthogonalität zu einer solchen euklidischen Ebene. Jede euklidische Ebene ist isomorph zu einer solchen Koordinatenebene über einem euklidischen Körper.

Bedeutung des Euklidischen Anordnungsaxioms

Seiner Form nach fordert das Euklidische Anordnungsaxiom nur, dass die Anordnung der Ebene, deren Existenz das Axiom fordert, mit der auf der pythagoreischen Ebene definierten Orthogonalitätsrelation verträglich sei. Es ist bemerkenswert, dass diese „anschaulich selbstverständliche“ Verträglichkeitsforderung impliziert, dass überhaupt nur eine Anordnung der Ebene möglich ist und dass die Ebene unter Konstruktionen mit Zirkel und Lineal abgeschlossen ist.

Eine „stark“ angeordnete, pappussche Ebene ist immer isomorph zu einer Koordinatenebene über einem geordneten Körper. Solche Körper enthalten immer wenigstens die zwei Quadratklassen und $Q_{-1}$ . Daher kann auf der Ebene stets eine Orthogonalitätsrelation definiert werden. (→Präeuklidische Ebene).
Die Orthogonalitätsrelation muss für eine pythagoreische Ebene so beschaffen sein, dass jeder Winkel der Ebene halbiert werden kann (die Ebene muss frei beweglich sein), also speziell jeder rechte Winkel, woraus die Existenz von Quadraten folgt und damit, dass die Orthogonalitätskonstante quadratisch äquivalent zu ist. (→Präeuklidische Ebene#Quadrate).
Gerade unter diesen Voraussetzungen existieren noch unendlich viele verträgliche Orthogonalitätsrelationen: Wählt man ein festes Bezugssystem , dann liefert jede Zahl im geordneten Körper als Orthogonalitätskonstante (bezogen auf dieses Koordinatensystem) eine andere Orthogonalitätsrelation! Jede dieser Orthogonalitätsrelationen führt in einer euklidischen Ebene aber, wenn man (E) zur Definition der Anordnung verwendet, zur gleichen Anordnung der Ebene.

Motivation

Die Beispiele für euklidische Körper machen deutlich, wodurch die Verallgemeinerung der reellen ebenen Geometrie motiviert ist: Die euklidischen Ebenen spiegeln wider, welche Konstruktionen bei bestimmten Vorgaben der Menge möglich sind. Figuren, die sich aus nicht mit Zirkel und Lineal konstruieren lassen, sind in der aus konstruierten euklidischen Ebene einfach nicht vorhanden! Während der reelle Abschluss von $\Q(M)$ sozusagen der größte über $\Q(M)$ algebraische Körper ist, auf dem eine euklidische Ebene (im Sinn der synthetischen Geometrie) aufgebaut werden kann, die die „Vorgabelängen“ enthält, sind die in den Beispielen genannten euklidischen Körper die kleinsten Körper mit diesen Eigenschaften.

Archimedische euklidische Ebene

Eine euklidische Ebene ist genau dann archimedisch angeordnet (kurz: archimedisch), erfüllt also das Axiom V.1 des Messens, wenn ihr Koordinatenkörper ein archimedischer (kurz für: archimedisch geordneter) Körper ist. Dies ist offensichtlich genau dann der Fall, wenn dieser euklidische Körper zu einem Teilkörper der reellen Zahlen isomorph ist. In diesem Fall gibt es – aufgrund der algebraisch eindeutig bestimmten Anordnung von − genau eine Einbettung $\iota: K\hookrightarrow\R$ und der Körper kann stets mit dem „reellen Modell“ $\iota(K)\subseteq \R$ identifiziert werden.

Ein „kleines“ und geometrisch allenfalls für Gegenbeispiele interessantes Modell eines nicht archimedischen euklidischen Körpers erhält man, wenn man den rationalen Funktionenkörper in einer Variablen $\Q(t)$ über den rationalen Zahlen (mit der Anordnung $-t<(\Q,<)<+t$ usw.) analog zu der oben für $\mathbb {Q}$ beschriebenen Konstruktion innerhalb seines algebraischen Abschlusses reellquadratisch abschließt.

Analytische Geometrie auf euklidischen Ebenen

In der analytischen Geometrie werden unter anderem

Normalformen für die affinen Selbstabbildungen eines affinen Raumes, speziell die Affinitäten auf diesem Raum,
Normalformen für quadratische Formen und die zugehörigen Quadriken

bestimmt. In beiden Aspekten verhält sich die euklidische Ebene über einem archimedischen euklidischen Körper , der hier mit seinem „reellen Modell“ identifiziert wird, im Wesentlichen wie die affine bzw. euklidische Ebene über $\mathbb {R}$ , denn ausschlaggebend ist hier die Existenz (oder Nichtexistenz) von Eigenwerten zu $2\times 2$ -Matrizen mit Einträgen aus . Eigenwerte, die hier die Nullstellen eines charakteristischen Polynoms vom Grad 2 sind, existieren für solche Matrizen genau dann in , wenn sie in $\mathbb {R}$ existieren! Jede $2\times 2$ -Matrix mit Einträgen aus , die reell diagonalisierbar ist, ist auch über diagonalisierbar, hat sie eine jordansche Normalform über $\mathbb {R}$ , dann ist sie auch über zu dieser jordanschen Normalform ähnlich.

Besonders für quadratische Formen und Quadriken ist bedeutsam, dass eine symmetrische $2\times 2$ -Matrix mit Einträgen aus durch eine Orthogonalmatrix mit Einträgen aus diagonalisiert werden kann. Die Eigenwerte dieser euklidischen Normalform sind dann entweder 0 oder quadratisch äquivalent zu −1 oder 1. Daher existieren in der euklidischen Ebene über ebenso viele affine Äquivalenzklassen von Quadriken, wie über der reellen Koordinatenebene. (→ Siehe Hauptachsentransformation)

Dies stimmt im Allgemeinen nur im zweidimensionalen affinen Raum über , also in der Ebene.

Ebenen mit Bogenmaß

Für eine übersichtliche Darstellung wird ein euklidischer Körper im Folgenden als Teilkörper von $\mathbb {R}$ aufgefasst, auch wenn analoge Konstruktionen auch für nicht archimedische euklidische Ebenen und Körper möglich sind. Die hier dargestellte Einführung eines Bogenmaßes bedeutet, dass auf einer Ebene, aus der Konstruktionen mit Zirkel und Lineal nicht herausführen, die also eine euklidische Ebene ist, ein zusätzliches Konstruktionswerkzeug „Winkelmesser“ eingeführt wird, mit dem es möglich ist, Bogenlängen (Winkelmaße) auf Strecken „abzuwickeln“.

Dazu wird die orientierte euklidische Ebene über mit der Zahlenebene $A=K(i)\subset \mathbb {R} (i)=\mathbb {C}$ identifiziert. Die Orientierung von und damit $\mathbb {R} ^{2}$ hat den technischen Zweck, dass die Identifizierung von $\mathbb {R} ^{2}$ mit $\mathbb {C}$ im richtigen Drehsinn erfolgt, so dass Drehungen im mathematisch positiven Sinn das richtige Vorzeichen erhalten. Eine Drehung $w_\alpha$ der Punktebene $\mathbb {R} ^{2}$ um den Ursprung kann dann durch die Multiplikation mit einer komplexen Zahl $z=e^{i\alpha}$ dargestellt werden:

$w_\alpha(x+iy)=e^{i\alpha}\cdot (x+iy)=(\cos\alpha+i\sin\alpha)\cdot(x+iy)$ .

Damit entspricht jede Drehung $w_\alpha$ der reellen Ebene um den Ursprung umkehrbar eindeutig einer Zahl $e^{i\alpha}=a+ib$ auf dem komplexen Einheitskreis $\mathbf E \R=\lbrace (a+ib)| a,b\in \R , a^2+b^2=1\rbrace$ . Dieser Einheitskreis ist zugleich als Untergruppe von $(\mathbb {C} ^{*},\cdot )$ isomorph zur Gruppe $D_O(\R^2)$ der Drehungen um den Ursprung und $\alpha$ liefert für die Drehung $w_\alpha$ um den Winkel $\alpha$ und damit für jeden orientierten Winkel ein (orientiertes) Bogenmaß (ein orientiertes Winkelmaß im üblichen Sinn) $\alpha$ , das bis auf die Addition von Vielfachen des Vollwinkelmaßes $2\pi$ eindeutig ist.

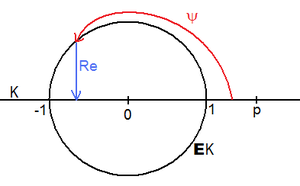
Die Gruppe der Drehungen der euklidischen Ebene $A\subset \mathbb {C}$ um den Ursprung ist isomorph zu der Untergruppe $\mathbf {E} K=\lbrace (a+ib)|a,b\in K,a^{2}+b^{2}=1\rbrace <\mathbf {E} \mathbb {R} <\mathbb {C} ^{*}.$

zur Definition des Bogenmaßes

Man definiert: Ein surjektiver Homomorphismus

$\psi: (K,+) \rightarrow\!\, ({\mathbf E} K,\cdot)$

mit der Eigenschaft, dass ein Element $p\in K, p>0$ existiert, so dass der Realteil $\operatorname{Re}(\psi)$ das Intervall $[0,p]\cap K$ bijektiv und streng monoton fallend auf das Intervall $[-1,1]\cap K$ abbildet und $\psi\left(p/2\right)=i$ ist, wird ein Bogenmaß auf der euklidischen Ebene genannt. Die Zahl heißt die Kreiszahl des Bogenmaßes.

Natürlich können bei jeder Koordinatenebene über einem Teilkörper von $\mathbb {R}$ die Drehungen und Winkel durch reelle Maßzahlen beschrieben werden. Das Entscheidende ist hier, dass jeder Klasse von gleich langen Strecken mit der Länge in der euklidischen Ebene, wobei $0\leq l<2p$ ist, durch das Bogenmaß umkehrbar eindeutig eine Drehung der Ebene $\psi(l)$ entspricht und die Addition von Zahlen, das heißt das Hintereinanderabtragen solcher Strecken mit der Komposition der zugehörigen Drehungen übereinstimmt!

Die Existenz eines Bogenmaßes ist ein zusätzliches Axiom in der synthetischen Geometrie für euklidische Ebenen, es wird auch als Winkelmesseraxiom bezeichnet. Seine Gültigkeit ist unabhängig von den übrigen Axiomen, die kleinste euklidische Ebene besitzt kein Bogenmaß, ebenso wenig die Ebene über dem Körper $\mathbb A \cap\R$ der reellen algebraischen Zahlen.

In einer orientierten, archimedisch angeordneten euklidischen Ebene mit Bogenmaß gibt es zu jeder Zahl $p\in K, p>0$ genau ein Bogenmaß, das als Kreiszahl hat. Dieses Bogenmaß bestimmt ein orientiertes Winkelmaß, das heißt für zwei Drehungen $\psi(l_1),\psi(l_2)$ ist $l_1\equiv\pm l_2 \;\operatorname{mod}\;2p$ genau dann, wenn sie gleich (für „“) bzw. invers zueinander (für „“) sind.

In der orientierten Ebene $\mathbb {R} ^{2}$ sind genau die Homomorphismen $\psi_c(t)=e^{ict},\; c>0$ Bogenmaße im Sinne der synthetischen Geometrie, ihre Kreiszahl ist dann $p=\pi/c$ .

In einer euklidischen Ebene mit Bogenmaß

existiert zu jeder natürlichen Zahl $n\geq 3$ ein regelmäßiges -Eck,
gibt es zu jeder Drehung $w_\alpha$ und jeder natürlichen Zahl $n\geq 1$ eine Drehung $w_{\alpha/n}$ mit $\left( w_{\alpha/n}\right)^n=w_\alpha$ .

Die zweite Aussage, die gelegentlich als Winkelteilungsaxiom bezeichnet wird, impliziert die erste. Beide Eigenschaften hat die kleinste euklidische Ebene nicht, während die euklidische Ebene über den reellen algebraischen Zahlen beide erfüllt. Sie sind also keine hinreichenden Bedingungen für die Existenz eines Bogenmaßes.

Hinreichend für die Existenz eines Bogenmaßes ist, dass die Einschränkungen der Winkelfunktionen $\cos$ und $\sin$ auf den euklidischen Körper nur Bilder in haben. Mit dieser Beobachtung lässt sich ein (als Menge) abzählbarer euklidischer Körper konstruieren, dessen Koordinatenebene ein Bogenmaß besitzt.

Literatur

Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.

Basierend auf einem Artikel in:

Wikipedia.de