Eine quadratische Form ist in der Mathematik
eine Funktion,
die sich in einigen Aspekten wie die quadratische
Funktion
verhält. Das bekannteste Beispiel ist das Quadrat des Betrages eines Vektors.
Quadratische Formen tauchen in vielen Bereichen der Mathematik auf. In der
Geometrie dienen sie dazu, Metriken
einzuführen, in der Elementargeometrie zur Beschreibung von Kegelschnitten. Sie sind
aber, falls zum Beispiel über den rationalen oder ganzen Zahlen betrachtet, auch
ein klassischer Gegenstand der Zahlentheorie,
in der man etwa nach den Zahlen fragt, die sich durch eine quadratische Form
darstellen lassen. Hier werden im Folgenden vor allem zahlentheoretische Aspekte
betrachtet.
Ein (reeller) Vektorraum
mit Skalarprodukt
lässt sich zu einem normierten
Raum machen, indem man die Norm
eines Vektors
als induzierte
Norm
definiert. Die hierbei verwendete Quadratwurzel stört insofern, als man, wenn
man stattdessen die Abbildung
betrachtet, auch auf allgemeinere Bilinearformen
und andere Grundkörper
verallgemeinern kann. Da ein Vektorraum dadurch bestimmt ist, dass Vektoren
addiert und mit Elementen des Grundkörpers skaliert werden können, ist zu
untersuchen, wie die Abbildung
sich hierbei verhält. Man findet die folgenden Beziehungen:
Abbildungen ,
die die obigen Bedingungen erfüllen, kann man auch betrachten, ohne dass sie von
einer Bilinearform herstammen. Obendrein kann man von Vektorräumen über einem
Körper zu Moduln
über einem kommutativen
Ring mit Einselement
verallgemeinern. Häufig untersucht man hierbei den Ring
der ganzen Zahlen sowie den Modul
,
insb.
.
Eine quadratische Form (in
Unbestimmten) über einem kommutativen
Ring mit Einselement
ist ein homogenes
Polynom vom Grad 2
in
Unbestimmten mit Koeffizienten in
.
Der Begriff Form wurde von Adrien-Marie Legendre geprägt.
Ein Quadratischer Raum ist ein Paar ,
bestehend aus einem A-Modul
und einer quadratischen Form
auf
.
Es bezeichne
die zu
gehörige symmetrische Bilinearform.
Dann heißen zwei Vektoren
-orthogonal
beziehungsweise
-orthogonal,
falls
gilt.
Im Folgenden sei angenommen, dass
in dem Ring
invertierbar
ist. Dies gilt insbesondere für Körper
der Charakteristik
ungleich 2 wie den reellen
oder komplexen Zahlen.
Ordnet man einer quadratischen Form
die Dreiecksmatrix
mit
,
sonst 0) zu, so kann man
auch als
beziehungsweise als
auffassen. Hieraus ergibt sich zunächst:
Es sei
ein
-Vektorraum. Nach dem Trägheitssatz
von Sylvester ist jede quadratische Form
diagonalisierbar, d.h. es existiert eine Basis
von
,
so dass
für gewisse
mit
gilt. Die Isomorphieklasse einer quadratischen Form wird also bestimmt durch
ihren Rang
und ihre Signatur
.
Quadratische Formen über
wurden von Hermann Minkowski
klassifiziert. Helmut Hasse
verallgemeinerte dies später auf eine Klassifikation von quadratischen Formen
über Zahlkörpern.
Insbesondere sind zwei quadratische Formen genau dann isomorph, wenn alle ihre
Vervollständigungen (reell, komplex und p-adisch) jeweils isomorph sind, Satz
von Hasse-Minkowski.
Man sagt, dass zwei positiv-definite
quadratische Formen
über
dasselbe Geschlecht haben, wenn man für alle
durch Erweiterung
mit Skalaren zu
(d.h. Tensorprodukt
mit
)
isomorphe quadratische Formen über
bekommt. Die Anzahl der Isomorphieklassen desselben Geschlechts kann mit der
Massenformel von Smith-Minkowski-Siegel bestimmt werden.
Zur Frage, ob eine vorgegebene ganzzahlige quadratische Form mit irgendwelchen ganzzahligen Argumenten einen vorgegebenen Wert annehmen kann („einen Wert darstellt bzw repräsentiert“), gibt es eine Vielzahl von Ergebnissen. Für sich betrachtet haben diese Ergebnisse naturgemäß oft anekdotischen Charakter. Beachtet man jedoch, dass
jeweils sowohl das Gitter
als auch die Menge der teilerfremden Zahlen in
bijektiv auf sich abbildet, so stehen die folgenden Ergebnisse jeweils für ganze
Familien äquivalenter Formen.
Prominent sind beispielsweise die folgenden Themen
Wenn zwei quadratische Formen durch Anwendung einer Matrix
auseinander hervorgehen, dann lässt sich eine ganze Zahl als Wert der einen
quadratischen Form darstellen genau dann, wenn sie sich als Wert der anderen
quadratischen Form darstellen lässt: dies folgt unmittelbar aus der Definition
.
Aus Sicht der Zahlentheorie sind die Formen
und
also äquivalent und es stellt sich die Frage, ein möglichst einfaches
Repräsentantensystem für die Menge der quadratischen Formen in n Variablen
modulo der Wirkung von
zu finden. Für quadratische Formen in 2 Variablen wurde dieses Problem von
Gauß in Kapitel 5 von „Disquisitiones
Arithmeticae“ (mit fast 260 Seiten der Hauptteil des Buches) diskutiert.
Im Fall positiv
definiter quadratischer Formen handelt es sich dabei in heutiger Sprache um
das Problem, einen Fundamentalbereich
für die Wirkung von
auf dem symmetrischen
Raum
(dem Raum der positiv definiten quadratischen Formen in n Variablen) zu
finden.
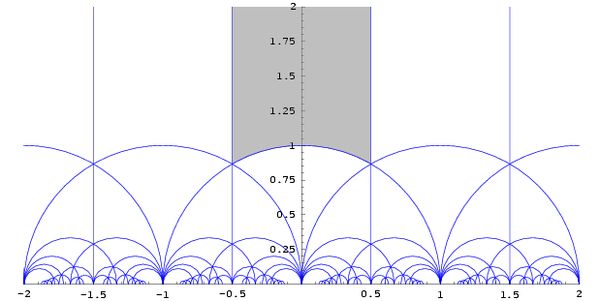
Für n=2 lässt sich der Raum
der positiv definiten binären
quadratischen Formen mit der hyperbolischen
Ebene identifizieren. Nebenstehendes Bild zeigt eine Zerlegung der
hyperbolischen Ebene in Fundamentalbereiche
für die Wirkung von
.
Ein solcher Fundamentalbereich (z.B. der im Bild grau schraffierte)
liefert also ein Repräsentantensystem von binären quadratischen Formen, so dass
jede andere positiv definite binäre quadratische Form äquivalent zu einer Form
aus dem Repräsentantensystem ist und insbesondere dieselben ganzen Zahlen
darstellt.
Verwandte Fragestellungen, allerdings außerhalb des Bereichs der
quadratischen Formen, sind Themen wie der Satz von
Fermat und das Waring
Problem.
Die (projektive) Nullstellenmenge einer quadratischen Form wird als Quadrik bezeichnet.

