Inversion (Geometrie)

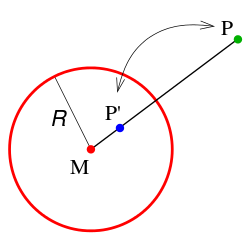
Definition der Inversion an einem Kreis bzw. einer Kugel mit Mittelpunkt und Radius :
$|\overline{MP'}|\cdot|\overline{MP}|= R^2$

Eine Inversion ist in der Geometrie entweder eine Kreisspiegelung oder eine Spiegelung an einer Kugel. Beide Begriffe sind an die der gewöhnlichen Spiegelung an einer Gerade in der Ebene oder einer Ebene im Raum angelehnt und haben, wie diese, die folgenden Eigenschaften:

a) Es gibt viele Fixpunkte: der Kreis/die Kugel, an dem/der gespiegelt wird, bleibt punktweise fest,

b) Winkel bleiben erhalten (insbesondere rechte Winkel),

c) Spiegelungen sind immer involutorisch, d.h., sie sind mit ihrer Umkehrabbildung identisch.

Es gibt allerdings wesentliche Unterschiede: 1) Eine Inversion bildet eine Gerade meistens auf einen Kreis ab. Sie ist also keine Kollineation. 2) Eine Inversion ist nicht längentreu.

Inversionen spielen schon lange eine wichtige Rolle in der Geometrie. Inverse Bilder von Kegelschnitten und Quadriken im Raum sind algebraische Kurven und Flächen von höchstens 4. Grad mit interessanten Eigenschaften (siehe Beispiele).

Definition und analytische Beschreibung

Eine Inversion an einem Kreis bzw. einer Kugel mit Mittelpunkt und Radius bildet einen von verschiedenen Punkt so auf einen Punkt ab, dass

auf der Halbgeraden liegt und
$|\overline{MP'}|\cdot|\overline{MP}|= R^2$ ist.

Die Spiegelung an einem Kreis mit Radius , dessen Mittelpunkt im Koordinatenursprung liegt, lässt sich durch

$(x,y) \mapsto \frac{R^2\cdot(x,y)}{x^2+y^2}$

bzw. im Raum die Spiegelung an der Kugel durch

$(x,y,z) \mapsto \frac{R^2\cdot(x,y,z)}{x^2+y^2+z^2}$

beschreiben.

In ebenen Polarkoordinaten $(r,\varphi )$ besitzt eine Kreisspiegelung eine besonders einfache Darstellung:

$(r,\varphi) \mapsto \left(\frac{R^2}{r},\varphi\right)$ .

Die Spiegelung am Einheitskreis ist dann

$(r,\varphi) \mapsto \left(\frac{1}{r},\varphi\right)$

und rechtfertigt die Bezeichnung Inversion.

Beschreibt man die reelle Ebene in üblicher Weise mit komplexen Zahlen, so lässt sich die Spiegelung am Einheitskreis durch die Abbildung

$z \mapsto \frac{1}{\overline z}$

darstellen. (Siehe hierzu auch Möbius-Ebene.)

Eigenschaften einer Inversion

Eine Kreisspiegelung besitzt folgende Eigenschaften:

Jeder Punkt des Inversionskreises ist ein Fixpunkt.
Eine Gerade durch den Mittelpunkt M des Inversionskreises wird auf sich abgebildet. Eine Gerade nicht durch M geht in einen Kreis durch M über. (s.u.)
Ein Kreis durch M wird auf eine Gerade nicht durch M abgebildet. Ein Kreis nicht durch M geht in einen Kreis nicht durch M über. (s.u.)
Winkel bleiben erhalten (Eine Kreisspiegelung ist eine konforme Abbildung). (s. Abschnitt Verallgemeinerung)
Eine Inversion ist eine Involution, d.h. sie ist mit ihrer Umkehrabbildung identisch. Sie vertauscht das Innere des Inversionskreises mit dem Äußeren.

Für die Spiegelung an einer Kugel ersetzt man in den obigen Eigenschaften Inversions"kreis" durch Inversions"kugel" und nimmt die folgenden Eigenschaften noch hinzu:

Ebenen durch den Ursprung werden auf sich, andere Ebenen werden auf Kugeln durch den Ursprung abgebildet. (s. unten)
Kugeln, die den Ursprung nicht enthalten, werden auf ebensolche abgebildet. Kugeln durch den Ursprung gehen in Ebenen, die den Ursprung nicht enthalten, über. (s. unten)

Inversionen (Kreisspiegelungen) von Kurven, Beispiele

Im Folgenden wird der Einfachheit halber angenommen, dass der Inversionskreis der Einheitskreis ist. Die Abbildungsvorschrift lautet dann

$(x,y)\mapsto (X,Y)={\frac {(x,y)}{x^{2}+y^{2}}}\quad {\text{und}}\quad (X,Y)\mapsto (x,y)={\frac {(X,Y)}{X^{2}+Y^{2}}}\ .$

Ist $u\mapsto (x(u),y(u))$ die Parameterdarstellung einer Kurve, so ist

$u\mapsto (X(u),Y(u))= \frac{(x(u),y(u))}{x(u)^2+y(u)^2}$

eine Parameterdarstellung der Bildkurve.

Ist f(x,y)=0 eine implizite Darstellung einer Kurve, so ist

$f\left(\frac{X}{X^2+Y^2}, \frac{Y}{X^2+Y^2} \right)=0$

eine implizite Darstellung der Bildkurve.

Inversion eines Kreises und zweier Geraden

Inversionen einer Parabel (links) und einer Hyperbel (rechts)

Inversion einer Parabel, Kardioide

Inversion einer Ellipse

Beispiel Gerade

Die Gerade mit der Gleichung ax+by+c=0 wird nach obiger Abbildungsvorschrift bei der Spiegelung am Einheitskreis auf die Kurve mit der Gleichung $a{\tfrac {X}{X^{2}+Y^{2}}}+b{\tfrac {Y}{X^{2}+Y^{2}}}+c=0$ abgebildet. Diese Gleichung ist äquivalent zu

und beschreibt im Fall c=0 die ursprüngliche Gerade, im Fall $c\neq 0$ einen Kreis durch den Nullpunkt mit der Gleichung

$\left(X+\frac{a}{2c}\right)^2+ \left(Y+\frac{b}{2c}\right)^2=\frac{a^2+b^2}{4c^2} \ .$

In den folgenden Beispielen werden der Einfachheit halber statt X,Y die (kleinen) x,y auch für die Bildkurve verwendet.

Beispiel Kreis

Der Kreis mit der Gleichung $(x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}$ wird nach obiger Abbildungsvorschrift bei der Spiegelung am Einheitskreis auf die Kurve mit der Gleichung $(\tfrac{x}{x^2+y^2}-x_0)^2+(\tfrac{y}{x^2+y^2}-y_0)^2=r^2$ abgebildet. Diese Gleichung ist äquivalent zu

und beschreibt
im Fall x_0^2+y_0^2=r^2 (der Urbildkreis geht durch den Nullpunkt) die Gerade

$2xx_0+2yy_0=1 \ .$

Falls $x_0^2+y_0^2\ne r^2$ ist, lässt sich obige Gleichung umformen zu

$\left(x-\frac{x_0}{x_0^2+y_0^2-r^2}\right)^2+\left(y-\frac{y_0}{x_0^2+y_0^2-r^2}\right)^2 =\frac{r^2}{(x_0^2+y_0^2-r^2)^2} \ .$

Diese Gleichung beschreibt einen Kreis.
Falls x_0=y_0=0 ist, ergibt sich wieder ein Kreis mit dem Nullpunkt als Mittelpunkt und Radius $1/r \ .$

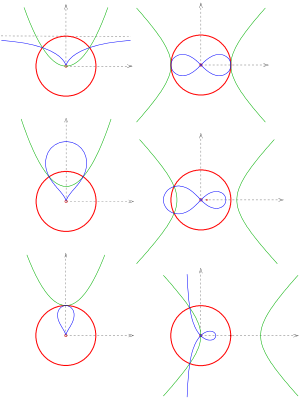
Beispiel Parabel

a) Die Parabel y=x^2 wird (durch Spiegelung am Einheitskreis) als parametrisierte Kurve (u,u^2) auf die Kurve $(\tfrac{1}{u(1+u^2)},\tfrac{1}{1+u^2})$ abgebildet (siehe Bild). Als implizite Kurve x^2-y=0 ergibt sich für die Bildkurve die Gleichung x^2-y(x^2+y^2)=0 , dies ist die Gleichung einer Zissoide.

b) Die Parabel $y=x^2-\tfrac{1}{4}$ wird durch die Kreisspiegelung auf die Kardioide mit der Gleichung (x^2+y^2+2y)^2=4(x^2+y^2) abgebildet. Die Inversion einer Parabel ergibt nur dann eine Kardioide, wenn das Inversionszentrum im Brennpunkt liegt.

Bei der Inversion einer Parabel gehen die Tangenten in eine Schar von Kreisen durch den Nullpunkt über, deren Einhüllende die Bildkurve ist. Im Fall der Kardioide liegen die Mittelpunkte dieser Kreise auch auf einem Kreis durch den Nullpunkt (in Beispiel b) hat dieser Kreis den Radius 1). Diese Eigenschaft verwendet man, um eine Kardioide als Einhüllende von Kreisen zu zeichnen: 1) Wähle einen Kreis k und einen Punkt O darauf, 2) Zeichne Kreise durch O mit Mittelpunkte auf k, 3) Zeichne die Einhüllende dieser Kreise.

Beispiel Hyperbel

a) Die Hyperbel mit der Gleichung $x^{2}-y^{2}=1$ wird durch die Spiegelung am Einheitskreis auf die Lemniskate mit der Gleichung (x^2+y^2)^2-(x^2-y^2)=0 abgebildet (siehe Bild).

b) Die Inversion der Hyperbel (x-1)^2-y^2=1 ergibt das kartesische Blatt x^2-2x(x^2+y^2)-y^2=0 (siehe Bild).

Kreisspiegelung auf der Riemannschen Zahlenkugel

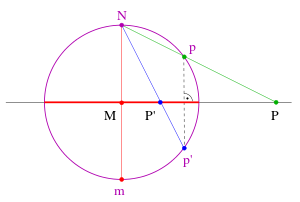
Kreisspiegelung auf der Riemannschen Zahlenkugel: den Punkten M, P, P' entsprechen die Punkte m,p,p' (magenta) auf der Kugel

Betrachtet man solch eine Zuordnung der reellen Ebene auf Punkte der Riemannschen Zahlenkugel, dass

die reelle Ebene die Äquatorebene und
der Einheitskreis dem Äquatorkreis entspricht,

so wird die Spiegelung am Einheitskreis als Abbildung auf der Riemannschen Zahlenkugel durch die gewöhnliche Spiegelung an der Äquatorebene vermittelt (siehe Bild). Dabei wird der Punkt mit dem Punkt vertauscht und Kreise durch gehen in Kreise durch über. Kreise durch $N = \infty$ entsprechen im ebenen Modell Geraden.

Hinweise zur Visualisierung impliziter Kurven findet man hier.

Inversion (Kugelspiegelung) von Ebenen, Kugeln, Geraden und Kreise

Analog zur Kreisspiegelung (s.o.) zeigt man rechnerisch, dass eine

Ebene auf eine Ebene oder Kugel (durch den Nullpunkt) und
Kugel auf eine Ebene (falls die Kugel durch den Nullpunkt geht) oder Kugel

abgebildet wird.

Da eine Gerade im Raum als Schnitt zweier Ebenen aufgefasst werden kann, geht eine Gerade in den Schnitt zweier Ebenen oder den Schnitt einer Ebene und einer Kugel oder den Schnitt zweier Kugeln über. D.h.

Das Bild einer Gerade ist entweder eine Gerade oder ein Kreis.

Da ein Kreis als Schnitt einer Ebene und einer Kugel aufgefasst werden kann, geht ein Kreis in den Schnitt einer Ebene und einer Kugel oder den Schnitt zweier Ebenen oder den Schnitt zweier Kugeln über. D.h.

Das Bild eines Kreises ist entweder wieder ein Kreis oder eine Gerade.
Eine Kugelspiegelung ist winkeltreu. (s. Abschnitt Verallgemeinerung.)

Inversionen von Flächen, Beispiele

Inversion einer Kugel

Inversion eines Ellipsoids

Inversion eines einschaligen Hyperboloids

Inversionen von Flächen bieten die Möglichkeit, Flächen mit vorhersehbaren Eigenschaften zu erzeugen. Da Kreise und Kugeln, die nicht durch den Ursprung (dem Inversionszentrum) gehen, wieder auf ebensolche abgebildet werden, bildet man einfache Flächen, die viele Kreise enthalten oder Kanalflächen sind, durch eine Inversion ab. Zum Beispiel sind die inversen Flächen von senkrechten Kreiszylindern, senkrechten Kreiskegeln und Rotationstori gerade die dupinschen Zykliden.

Parameterdarstellungen bzw. implizite Darstellungen ergeben sich analog zum Kurvenfall (siehe oben).

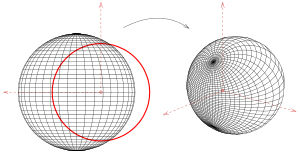
Beispiel Kugel mit Längen- und Breitenkreise

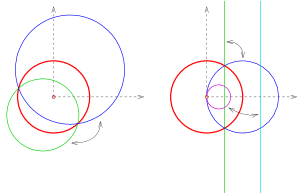
Die für eine Inversion einfachste Fläche ist eine Kugel mit Längen- und Breitenkreisen. Das Bild der Kugel ist wieder eine Kugel und die Längen- und Breitenkreise gehen wieder in ein System von sich orthogonal schneidenden Kreisen über. Die Bilder von Nord- und Südpol liegen allerdings im Allgemeinen nicht mehr auf einem Kugeldurchmesser (siehe Bild).

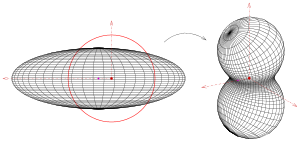
Beispiel Ellipsoid mit Kreise und Ellipsen

Auf einem Rotationsellipsoid liegt eine Schar von horizontalen Kreisen, die bei dem im Bild gezeigten Beispiel wieder auf Kreise abgebildet werden. Die senkrechten Ellipsen des Ellipsoids werden auf Kurven abgebildet, die ähnlich der oben im Beispiel einer Kreisspiegelung einer Ellipse sind.

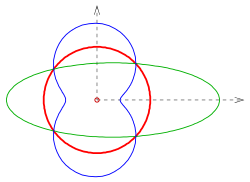
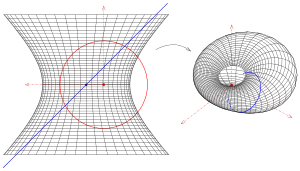
Beispiel einschaliges Hyperboloid mit Kreise und Hyperbeln

Auf einem einschaligen Rotationshyperboloid liegt eine Schar von Kreisen (im Bild sind es horizontale Kreise) und zwei Scharen von Geraden (im Bild ist eine Gerade (blau) dargestellt). Die Kreise gehen wieder in eine die Fläche überdeckende Schar von Kreisen über. Auch jede Gerade (Erzeugende) des Hyperboloids geht in einen Kreis durch den Ursprung über (s. Bild). Die Schar von Hyperbeln (sie schneiden die Kreise orthogonal) wird auf eine Schar von Lemniskaten-ähnlichen Kurven, die den Ursprung enthalten, abgebildet. Im Bild sind nur diese Teile dieser Kurven dargestellt, die sich als Bilder der Hyperbelbögen ergeben.

Hinweise zur Visualisierung impliziter Flächen findet man hier.

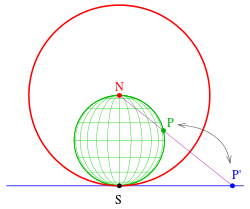
Stereografische Projektion als Inversion einer Kugel

Stereografische Projektion eines Quadrat-Netzes (in der Ebene)

Stereografische Projektion als Inversion

Bei der Stereografischen Projektion projiziert man die Punkte einer Kugel von einem Kugelpunkt aus auf die Tangentialebene des gegenüber liegenden Punktes (s. Bild). Diese Abbildung lässt sich als Inversion einer Kugel auf eine Ebene auffassen. Hat die Kugel, die abgebildet wird, die Gleichung $x^2+y^2+(z+\tfrac{1}{2})^2=\tfrac{1}{4}$ (Mittelpunkt $(0,0,-0{,}5)$ , Radius 0{,}5 , im Bild grün), so wird sie bei der Inversion an der Einheitskugel (im Bild rot) auf die Tangentialebene im Punkt S=(0,0,-1) abgebildet. Die Geraden durch das Inversionszentrum werden auf sich abgebildet. Sie sind die Projektionsstrahlen der Stereografischen Projektion. Die im Bild sichtbaren Längenkreise der Kugel werden auf Geraden (der Tangentialebene im Südpol S) durch S abgebildet. Die Breitenkreise gehen in konzentrische Kreise mit Mittelpunkt S über.

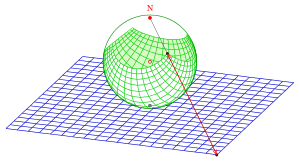
Beispiel Quadratnetz: Das zweite Bild zur Stereografischen Projektion zeigt die Projektion eines ebenen Quadratnetzes in der Tangentialebene des Südpols auf die Kugel. Da Geraden der Ebene auf Kreise durch den Nordpol abgebildet werden, entstehen durch das Netz zwei Scharen von solchen Kreisen, die im Nordpol jeweils dieselbe Tangente besitzen. Da eine Inversion und damit auch eine Stereografische Projektion winkeltreu ist (s.u.), berühren sich die Kreise (in N) oder schneiden sich senkrecht in N und einem weiteren Punkt.

Verallgemeinerung

Der Begriff der Inversion lässt sich analog zum 2-dimensionalen Fall auf einen n-dimensionalen euklidischen Raum übertragen und analytisch durch

$\vec x \mapsto \frac{R^2\cdot\vec x}{|\vec x|^2}$

beschreiben.

Bilder von Hyperebenen und Hyperkugeln

Wie beim Beweis, dass eine Kreisspiegelung Geraden und Kreise in ebensolche abbildet, zeigt man mit Hilfe der Vektorrechnung, dass im allgemeinen Fall gilt:

Bei einer Inversion gehen Hyperebenen und Hyperkugeln in ebensolche über.

Winkeltreue

Es sei $\vec x=\vec c\;(s)$ eine reguläre Kurve im $\mathbb {R} ^{n}$ und $\vec x=\vec \gamma\;(s)=\tfrac{\vec c\;(s)}{\vec c\;^2(s)}$ die dazu inverse Kurve bezüglich der Spiegelung an der Einheitshyperkugel. Dann gilt

$\vec\gamma\;'=\frac{\vec c\;'\vec c\;^2-2\vec c(\vec c\cdot\vec c\;')}{(\vec c\;^2)^2}\ .$ (Das Argument (s) wurde jeweils weggelassen.)

Analog gilt für eine weitere reguläre Kurve $\vec x=\vec d(t)$ und ihre Inverse $\vec x=\vec \delta(t)=\tfrac{\vec d(t)}{\vec d\;^2(t)}$ :

$\vec\delta\;'=\frac{\vec d\;'\vec d\;^2-2\vec d(\vec d\cdot\vec d\;')}{(\vec d\;^2)^2}\ .$

Beide Kurven mögen nach der Bogenlänge parametrisiert sein (d.h. es ist $|\vec c\;'|=|\vec d\;'|=1$ ) und sich im Punkt $\vec c(0)=\vec d(0)$ schneiden. Dann schneiden sich ihre Inversen in $\vec \gamma(0)=\vec \delta(0)$ . In diesen Schnittpunkten gilt also in den obigen Formeln ${\vec {c}}={\vec {d}}\$ und man rechnet nach, dass

$({\vec {\gamma }}\;')^{2}=\dots ={\frac {1}{({\vec {c}}\;^{2})^{2}}}=({\vec {\delta }}\;')^{2}\ .$

Unter Beachtung, dass ${\vec {c}}={\vec {d}}\$ ist, ergibt sich für den Schnittwinkel $\alpha$ der Bildkurven:

$\cos \alpha ={\frac {{\vec {\gamma }}\;'}{|{\vec {\gamma }}\;'|}}\cdot {\frac {{\vec {\delta }}\;'}{|{\vec {\delta }}\;'|}}=({\vec {\gamma }}\;'\cdot {\vec {\delta }}\;')\;({\vec {c}}\;^{2})^{2}=\dots ={\vec {c}}\;'\cdot {\vec {d}}\;'\ .$

Also ist der Schnittwinkel der inversen Kurven identisch mit dem Schnittwinkel der gegebenen Kurven.

Literatur

F. Borges: Die Spiegelung am Kreis. Books on Demand, Norderstedt, 2015, ISBN 978-3-7347-9186-4.
L. Felix: Elementarmathematik in moderner Darstellung. Vieweg-Verlag, 1969, ISBN 978-3-322-96093-1.
K. Fladt: Analytische Geometrie spezieller Flächen und Raumkurven. Vieweg-Teubner-Verlag, ISBN 978-3-528-08278-9.
T. Needham: Anschauliche Funktionentheorie. Oldenbourg-Verlag, 2001, ISBN 3-486-24578-3.
H. Schmidt: Die Inversion und ihre Anwendungen, 1950, Oldenbourg-Verlag.

Basierend auf einem Artikel in:

Wikipedia.de