
Kardioide
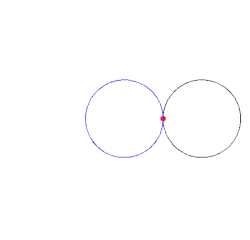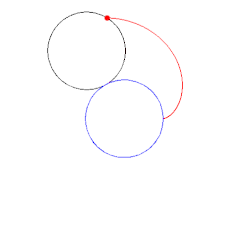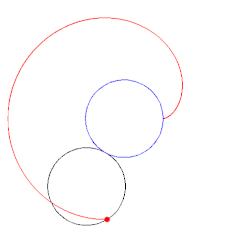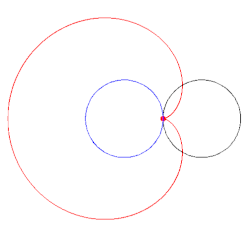
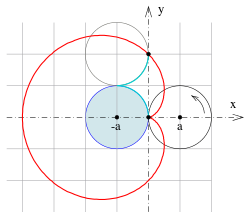
Die Kardioide oder Herzkurve (von griechisch καρδία ‚Herz‘; englisch:Cardioid) ist eine ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung, die ihren Namen wegen ihrer Form erhielt.
Lässt man auf der Außenseite eines gegebenen festen Kreises mit
Mittelpunkt M und Radius
einen weiteren Kreis mit dem gleichen Radius abrollen und betrachtet man dabei
einen bestimmten Punkt P auf dem abrollenden Kreis, so beschreibt P eine
Kardioide. Damit erweist sich die Kardioide als spezielle Epizykloide.
Gleichungen der Kardioide
Ist
der gemeinsame Radius der erzeugenden Kreise mit den Mittelpunkten
,
der Rollwinkel und der Nullpunkt der Startpunkt (s. Bild), so erhält man die
- Parameterdarstellung:
.
Hieraus ergibt sich die Darstellung in
Mit der Substitution
und
erhält man nach Beseitigung der Wurzel die implizite Darstellung in
.
- Beweis der Parameterdarstellung
Der Beweis der Parameterdarstellung lässt sich mit Hilfe komplexer Zahlen und
ihrer Darstellung als Gaußsche
Zahlenebene leicht führen. Die Rollbewegung des schwarzen Kreises auf dem
blauen Kreis kann man in die Hintereinanderausführung zweier Drehungen zerlegen.
Die Drehung eines Punktes
(komplexe Zahl) um den Nullpunkt
mit dem Winkel
wird durch die Multiplikation mit
bewirkt.
- Die Drehung
um den Punkt
ist
.
- Die Drehung
um den Punkt
ist
.
Ein Kardioidenpunkt
entsteht durch Drehung des Nullpunktes um
und anschließende Drehung um
jeweils um den Winkel
:
.
hieraus ergibt sich
(Es wurden die Formeln
benutzt. Siehe Formelsammlung
Trigonometrie.)
Flächeninhalt, Kurvenlänge und Krümmungsradius
Für die obige Kardioide ist
- der Flächeninhalt
, und
- die Kurvenlänge
.
- Krümmungsradius
Die Beweise verwenden jeweils die Polardarstellung der obigen Kardioide. Formeln für den Flächeninhalt und die Kurvenlänge findet man z.B. hier.
- Beweis für den Flächeninhalt
.
- Beweis für die Kurvenlänge
.
- Beweis für den Krümmungsradius
Der Krümmungsradius
einer Kurve in Polarkoordinaten
ist (s. Krümmung)
Für die Kardioide
ergibt sich
Eigenschaften der Kardioide
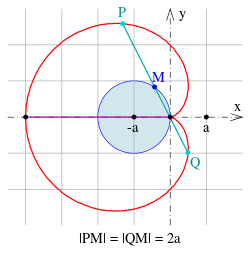
Sehnen durch die Spitze
- S1: Die Sehnen durch die Spitze der Kardioide haben alle
dieselbe Länge
.
- S2: Die Mittelpunkte der Sehnen durch die Spitze liegen auf dem festen Erzeugerkreis (s. Bild).
- Beweis zu S1
Die Punkte
liegen auf einer Sehne durch die Spitze (=Nullpunkt). Es ist
-
.
-
- Beweis zu S2
Für den Beweis wird die Darstellung in der gaußschen Zahlenebene (s. o.) verwendet. Für die Punkte
,
ist
der Mittelpunkt der Sehne
und liegt auf dem Kreis der Gaußschen Zahlenebene mit Mittelpunkt
und Radius
(s. Bild).
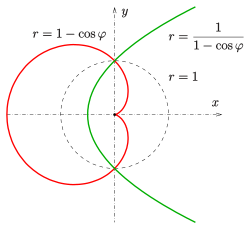
Kardioide als inverse Kurve einer Parabel
- Die Kardioide ist das Bild einer Parabel unter einer Kreisspiegelung (Inversion), bei der das Inversionszentrum im Brennpunkt der Parabel liegt (s. Bild).
Im Beispiel des Bildes haben die Erzeugerkreise den Radius .
Die gespiegelte Parabel genügt in x-y-Koordinaten der Gleichung
.
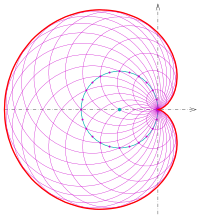
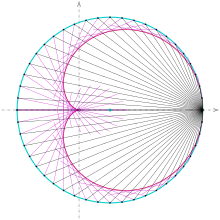
Kardioide als Einhüllende einer Kreisschar
Bildet man bei der Inversion der Parabel im vorigen Abschnitt die Tangenten mit ab, so gehen sie als Geraden in eine Schar von Kreisen durch das Inversionszentrum (Nullpunkt) über. Eine genauere Untersuchung (Nachrechnen) zeigt: Die Mittelpunkte der Kreise liegen alle auf dem festen Erzeugerkreis (cyan) der Kardioide. Der Erzeugerkreis ist das Bild der Leitlinie der Parabel. Da sich auf der Leitlinie einer Parabel die Tangenten senkrecht schneiden und die Kreisspiegelung winkeltreu ist, schneiden sich Kreise der Kreisschar auf dem Erzeugerkreis auch senkrecht.
Die hier beschriebene Eigenschaft der Kreisschar erlaubt eine einfache Methode um eine Kardioide zu zeichnen:
- 1) Wähle einen Kreis k und einen Punkt O darauf,
- 2) zeichne Kreise durch O mit Mittelpunkte auf k,
- 3) zeichne die Einhüllende dieser Kreise.
- Beweis mit Einhüllenden-Bedingung
Es sei durch
eine Schar von impliziten Kurven mit dem Scharparameter
gegeben. Die Einhüllende (oder Hüllkurve) besteht aus Punkten
,
die für festes
Lösungen des i.a. nicht linearen Gleichungssystems
(Einhüllenden-Bedingungen)
sind. (
bedeutet die partielle
Ableitung nach
,
siehe Einhüllende)
Es sei k der Kreis mit Mittelpunkt
und Radius
.
k hat die Parameterdarstellung
.
Die Kreisschar, deren Mittelpunkte auf k liegen und die durch den Punkt
gehen, lassen sich implizit durch
beschreiben. Multipliziert man die Klammern aus, ergibt sich
Die 2. Scharbedingung ist
Man prüft leicht nach, dass die Punkte der Kardioide mit der Parameterdarstellung
das nicht lineare Gleichungssystem erfüllt. Der Scharparameter
ist hier identisch mit dem Winkel-Parameter der Kardioide.
Kardioide als Einhüllende einer Geradenschar
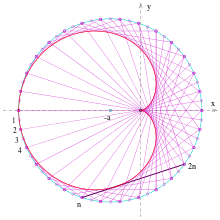
Eine ähnlich einfache Methode, eine Kardioide als Einhüllende einer Geradenschar zu konstruieren, geht auf L. Cremona zurück:
- Zeichne einen Kreis, unterteile ihn gleichmäßig mit
Punkten (s. Bild) und nummeriere diese fortlaufend.
- Zeichne die Sehnen:
. (Man kann es so ausdrücken: Der zweite Punkt der Sehne bewegt sich mit doppelter Geschwindigkeit.)
- Die Einhüllende dieser Strecken ist eine Kardioide.

- Beweis
Im Folgenden werden die trigonometrischen
Formeln für
verwendet. Um die Rechnungen einfach zu halten, wird der Beweis für die
Kardioide mit der Polardarstellung
geführt (s. Abschnitt anders orientierte Kardioiden).
- Gleichung der Tangente
- an die Kardioide mit der Polardarstellung
:
- Aus der Parameterdarstellung
berechnet man zunächst den Normalenvektoren .
Die Gleichung der Tangente
ist dann:
Mit Hilfe der trigonometrischen Formeln und der anschließenden Division durch
lässt sich die Gleichung der Tangente so schreiben:
- Gleichung der Sekante
- an den Kreis mit Mittelpunkt
und Radius
: Für die Gleichung der Sekante durch die beiden Punkte
ergibt sich:
Mit Hilfe der trigonometrischen Formeln und der anschließenden Division durch
lässt sich die Gleichung der Sekante so schreiben:
Die beiden Winkel
haben zwar verschiedene Bedeutungen (s. Bild), für
ergibt sich aber dieselbe Gerade. Also ist auch jede obige Sekante an den Kreis
eine Tangente der Kardioide und
- die Kardioide ist die Einhüllende der Kreissehnen.
Bemerkung:
Der Beweis lässt sich auch mit den Einhüllen-Bedingungen
einer impliziten Kurvenschar (s. vorigen Abschnitt) führen. Dabei beschreibt
die Schar der Sekanten an den Kreis (s.o.)
Beide Gleichungen sind für festen Parameter t Geradengleichungen. Der Schnittpunkt
der Geraden ist ein Punkt der Kardioide mit der Polardarstellung .
(Bei Umformungen müssen immer wieder trigonometrische Formeln (s.o.)
benutzt werden.)
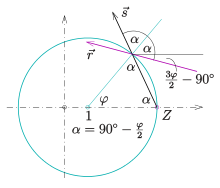
Lichtquelle
Kardioide als Kaustik eines Kreises
Die vorigen Überlegungen liefern auch einen Beweis dafür, dass als Kaustik eines Kreises mit der Lichtquelle auf dem Kreis eine Kardioide auftritt.
- Gehen in der Ebene von einem Punkt
eines spiegelnden Kreises Lichtstrahlen gemäß der Abbildung aus, so sind die im Innern des Kreises reflektierten Lichtstrahlen die Tangenten einer Kardioide. (s. Abschnitt Kardioide in Optik und Akustik)
- Beweis
Der Kreis habe (wie im vorigen Abschnitt) den Mittelpunkt
und den Radius
.
Der Kreis hat dann die Parameterdarstellung
Die Tangente im Kreispunkt
hat den Normalenvektor
.
Der reflektierte Strahl muss dann (laut Abbildung) den Normalenvektor
haben und durch den Kreispunkt
gehen. Der reflektierte Strahl liegt also (s. vorigen Abschnitt) auf der Gerade
mit der Gleichung
die wiederum Tangente an die Kardioide mit der Polardarstellung
des vorigen Abschnitts ist.
Bemerkung: Mehrfachreflexionen am Kreis werden bei diesen Überlegungen üblicherweise nicht berücksichtigt.
Kardioide als Fußpunktkurve eines Kreises
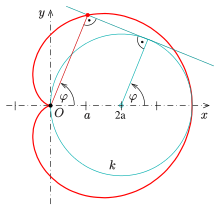
Die Cremona-Erzeugung einer Kardioide sollte nicht verwechselt werden mit der folgenden Erzeugung:
Es sei ein Kreis
und ein fester Punkt
auf diesem Kreis gegeben. Es gilt:
- Die Lotfußpunkte vom Punkt
auf die Tangenten des Kreises
bilden eine Kardioide.
Eine Kardioide ist somit eine spezielle Fußpunktkurve (engl.: pedal curve) eines Kreises.
- Beweis
In der x-y-Ebene habe der Kreis
den Mittelpunkt
und den Radius
.
Die Tangente im Kreispunkt
hat die Gleichung
Der Lotfußpunkt von
auf die Tangente ist der Punkt
mit dem noch unbekannten Abstand
zum Nullpunkt
.
Einsetzen in die Tangentengleichung ergibt
die Polardarstellung einer Kardioide.
Bemerkung: Liegt der Punkt
nicht auf dem Kreis
,
so entsteht eine pascalsche Schnecke (s. nächsten Abschnitt).
Kardioide als pascalsche Schnecke
Eine pascalsche Schnecke ist eine ebene Kurve mit einer Polardarstellung
.
Im Fall
ergibt sich eine Kardioide. Also gilt:
- Die Kardioide ist ein Spezialfall der pascalschen Schnecke, diese ist wiederum ein Spezialfall der Konchoide.

Kardioide in Optik und Akustik
- Die Lichterscheinung (Kaustik) in einer Kaffeetasse, die von Licht aus einer am Tassenrand platzierten Lichtquelle getroffen wird, ist eine Kardioide. Die Kaustik, die von parallel eintreffendem Licht erzeugt wird, wird allerdings durch eine andere Kurve (Nephroide) beschrieben; in anderen Fällen entsteht eine Mischform.
In der Tontechnik wird das Polardiagramm der Richtcharakteristik einer Kardioide mit Niere bezeichnet, auch wenn es eine Herzkurve darstellt.
Evolute einer Kardioide
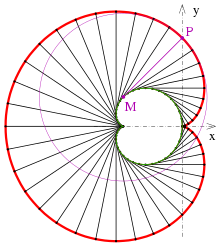
magenta: ein Punkt P, sein Krümmungsmittelpunkt M und der zugehörige Krümmungskreis
Die Evolute einer ebenen Kurve ist
der geometrische Ort aller Krümmungsmittelpunkte
dieser Kurve. Für eine parametrisierte Kurve
mit Krümmungsradius
hat die Evolute die Parameterdarstellung
wobei
die geeignet orientierte Einheitsnormale ist. (
zeigt zu dem Krümmungsmittelpunkt hin.)
Für eine Kardioide gilt:
- Die Evolute einer Kardioide ist wieder eine Kardioide ein Drittel so groß (siehe Bild).
- Beweis
Für die Kardioide mit der Parameterdarstellung
ist die Einheitsnormale
und der Krümmungskreisradius (s. oben)
Also hat die Evolute die Parameterdarstellung
Diese Gleichungen beschreiben eine Kardioide, die ein Drittel so groß wie die
gegebene Kardioide, um 180 Grad gedreht und um
entlang der x-Achse verschoben ist.
(Es wurden trigonometrische
Formeln benutzt: .)
Orthogonaltrajektorien
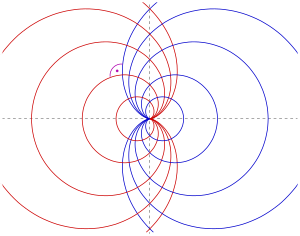
Eine Orthogonaltrajektorie einer Kurvenschar ist eine Kurve, die jede Kurve der Schar senkrecht schneidet. Für Kardioiden gilt:
- Die Orthogonaltrajektorien der Kardioidenschar mit den Gleichungen
-
- sind die Kardioiden mit den Gleichungen
(Die zweite Schar entsteht durch Spiegelung der ersten an der y-Achse. Siehe Bild.)
Beweis:
Ist eine Kurve in Polarkoordinaten durch eine Funktion
gegeben, so besteht zwischen den kartesischen Koordinaten und den
Polarkoordinaten eines Punktes die folgende Beziehung:
und damit
Dividiert man die letzten beiden Gleichungen erhält man die Steigung in kartesischen Koordinaten:
Für die Kardioiden mit den Gleichungen
bzw.
ergibt sich
bzw.
(Die Steigungen hängen jeweils nur von
ab, und nicht mehr von den Parametern
!)
Hieraus ergibt sich
D.h. jede Kurve der einen Schar schneidet jede Kurve der anderen Schar senkrecht.
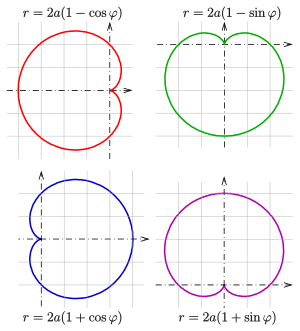
Anders orientierte Kardioiden
Wählt man andere Lagen der Kardioide im Koordinatensystem so ändern sich die Gleichungen, die sie beschreiben. Im Bild sind die 4 üblichen Orientierungen und ihre zugehörigen Polardarstellungen zu sehen.
Zur Geschichte der Kardioide
Bei der Suche nach einer optimalen Form von Zahnrädern untersuchte Ole Roemer 1674 Epizykloiden und damit auch Kardioiden. Der Name Kardioide wurde zuerst von Johann Francesco Melchiore Salvemini Castillon verwendet. Die Länge einer Kardioide wurde 1708 von Philippe de la Hire berechnet. Eine Kardioide ist eine spezielle Pascalsche Schnecke, benannt nach Étienne Pascal, dem Vater von Blaise Pascal.
Literatur
- Kleine Enzyklopädie Mathematik. Harri Deutsch-Verlag, 1977, ISBN 3-87144-323-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.12. 2021