
Evolute
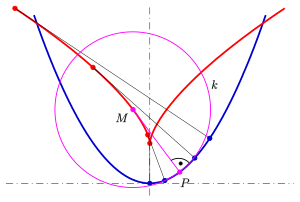
Die Evolute einer ebenen Kurve ist
- die Bahn, auf der sich der Mittelpunkt des Krümmungskreises bewegt, wenn der zugehörige Punkt die gegebene Kurve durchläuft.
Oder auch:
Evoluten stehen in engem Zusammenhang mit den Evolventen einer gegebenen Kurve, denn es gilt: Eine Kurve ist die Evolute jeder ihrer Evolventen.
Evolute einer parametrisierten Kurve
Beschreibt
eine reguläre
Kurve in der euklidischen Ebene, deren Krümmung nirgends 0 ist, und sind
der Krümmungskreisradius
und
die zum Krümmungsmittelpunkt weisende Einheitsnormale, so ist
die Evolute der gegebenen Kurve.
Ist
und
,
so ist
und
.
Eigenschaften der Evolute
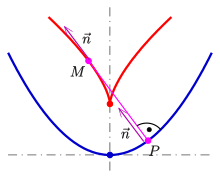
Um Eigenschaften einer regulären Kurve herzuleiten, ist es vorteilhaft, die
Bogenlänge
der gegebenen Kurve als Parameter
zu verwenden. Denn dann gilt (s. Frenetsche
Formeln)
und
.
Hieraus folgt für den Tangentenvektor der Evolute
:
Aus dieser Gleichung ergeben sich die folgenden Eigenschaften einer Evolute:
- Die Evolute ist in Punkten mit
nicht regulär, d.h., sie hat in Punkten maximaler oder minimaler Krümmung Spitzen (s. Parabel, Ellipse, Nephroide).
- Die Normalen der gegebenen Kurve sind Tangenten der Evolute, d.h.: Die Evolute ist die Einhüllende der Normalen der gegebenen Kurve.
- In Abschnitten der gegebenen Kurve, in denen
bzw.
gilt, ist sie eine Evolvente ihrer Evolute. (Im Bild ist die blaue Parabel eine Evolvente der roten Neilschen Parabel.)
Beweis der letzten Eigenschaft:
In dem betrachteten Abschnitt sei
.
Eine Evolvente der Evolute lässt
sich folgendermaßen beschreiben:
wobei
eine Fadenverlängerung bedeutet (s. Evolvente).
Mit
und
ergibt sich
D. h., für die Fadenverlängerung
erhält man die gegebene Kurve wieder.
- Parallele Kurven besitzen dieselbe Evolute.
Beweis: Eine zur gegebenen Kurve im Abstand
parallele Kurve besitzt die Parameterdarstellung
und den Krümmungsradius (s. Parallelkurve)
.
Die Evolute der Parallelkurve ist also
Beispiele
Evolute der Normalparabel
Die Normalparabel lässt sich durch die Parameterdarstellung
beschreiben. Nach den obigen Formeln ergeben sich für die Evolute die folgenden
Gleichungen:
Dies ist die Parameterdarstellung einer Neilschen Parabel.
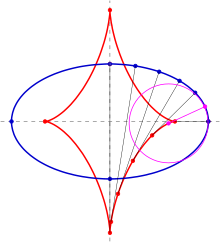
Evolute einer Ellipse
Für die Ellipse mit der Parameterdarstellung
ergibt sich:
Diese Gleichungen beschreiben eine schiefe Astroide.
Elimination von
liefert die implizite Darstellung
Evoluten bekannter Kurven
- Zu einer Astroide: wiederum eine Astroide (doppelt so groß)
- Zu einer Ellipse: eine schiefe Astroide
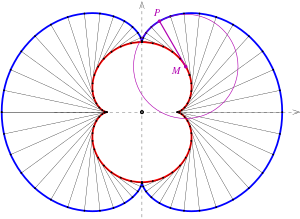
- Zu einer Kardioide: wiederum eine Kardioide (ein Drittel so groß)
- Zu einem Kreis: ein Punkt, nämlich dessen Mittelpunkt
- Zu einer Deltoide: wiederum eine Deltoide (dreimal so groß)
- Zu einer Zykloide: eine kongruente Zykloide
- Zu einer Epizykloide: eine vergrößerte Epizykloide
- Zu einer Hypozykloide: eine ähnliche Hypozykloide
- Zu einer logarithmischen Spirale: die gleiche logarithmische Spirale
- Zu einer Nephroide: wiederum eine Nephroide (halb so groß)
- Zu einer Parabel: eine Neilsche Parabel
- Zu einer Traktrix: eine Katenoide (Kettenlinie)
Literatur
- K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und … Springer-Verlag, 2012, ISBN 3-8348-8346-8.
- Kleine Enzyklopädie Mathematik. Harry Deutsch Verlag, 1977, ISBN 3-87144-323-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.12. 2021