
Traktrix

Traktrix (v. lat. trahere „ziehen, schleppen“, pl. Traktizes), auch Schleppkurve, Ziehkurve, Zugkurve, Treidelkurve, ist eine spezielle ebene Verfolgungskurve. Der Name erklärt sich daraus, dass diese Kurve von einem Massenpunkt beschrieben wird, der mit einem ihn ziehenden Punkt verbunden ist, der sich im rechten Winkel zur ursprünglichen Verbindungslinie der beiden Punkte bewegt.
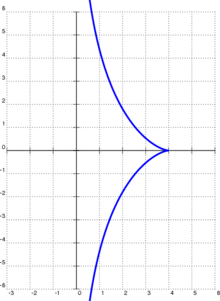
Die eigentliche (gerade) Traktrix ist die Kurve, bei der für jede Tangente der Abschnitt zwischen dem Berührpunkt und der Koordinatenachse konstant ist. Man nennt sie auch Huygens-Traktrix, nach Christiaan Huygens, der das zugrunde liegende Problem 1693 löste, nachdem es von Claude Perrault 1670 und Isaac Newton 1676 beschrieben wurde. Sie ist eine der Kurven, die mit dem Trivialnamen Hundekurve bezeichnet werden. Diese Kurve spielt in der hyperbolischen Geometrie eine wichtige Rolle.
Schon Leonhard Euler und andere beschäftigten sich bald darauf mit der allgemeinen Traktrix, die beliebige Leitkurven erlaubt. Sie spielt eine wichtige Rolle in der Modellierung des Fahrverhaltens, nämlich der Rückwärtsfahrt und dem Verhalten beim Durchfahren einer Kurve. Die daraus gewonnenen Erkenntnisse werden beim Entwurf von Straßen verwendet, um deren Befahrbarkeit zu überprüfen.
Eigentliche Traktrix
- Bildungsgesetz
- Sei
der Startpunkt eines „Ziehenden“, und
der Startpunkt eines „Gezogenen“ sowie
der Abstand
.
- Wandert der Punkt
auf einer Geraden, und „folgt“ ihm der Punkt
in konstantem Abstand
, dann durchläuft
eine Traktrix.
- Funktionsgleichung in Kartesischen Koordinaten
im Ursprung,
auf der x-Achse,
bewegt sich entlang der y-Achse:
Eine explizite Darstellung nach x(y) ist hierbei nicht möglich.
- mit
ergibt sich eine elegante Form (mit sech
):
- mit
, dem Winkel zwischen x-Achse und Tangente – erfordert keine Hyperbelfunktion:
- mit
, eine Darstellung, die die Arbeit mit tabellierten Werten erleichtert:
Herleitung
Im Folgenden sei die Kurve in 1. Hauptlage betrachtet:
wandert entlang der x-Achse, mit
:
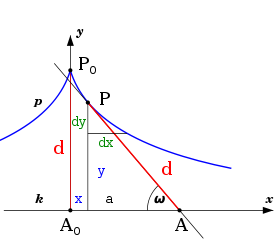
- Mit
lässt sich aus dem Bildungsgesetz direkt folgende Differentialgleichung (Tangentenbedingung) ablesen:
- Die Lösung gelingt mit der Substitution
. Dies entspricht der oben erwähnten Parameterdarstellung:
.
- Es folgt
und dann durch Trennung der Variablen
Integration liefert
und Rücksubstitution:
Eigenschaften
- Offensichtlich ist
. Ist
liegt der Graph spiegelverkehrt zur y-Achse.
- Für
fallen beide möglichen Tangenten mit der y-Achse zusammen, der Punkt
ist also eine eigentliche Spitze.
- Die Länge
der Kurve zwischen
und
errechnet sich zu:
- Die Fläche unter der Traktrix:
- Die Evolute der Traktrix ist die
Katenoide
- Wird diese Kurve um die x-Achse rotiert, so entsteht die Pseudosphäre, welche in der hyperbolischen Geometrie die Rolle der Kugel einnimmt. So ist etwa die Fläche unter der Traktrix dieselbe wie beim Halbkreis. Die Traktrix ist hierbei als Geodäte die Entsprechung der Geraden im „normalen“ (euklidischen) Raum.
Allgemeine Traktrix
Der Begriff der Traktrix lässt sich verallgemeinern:
- Gegeben seien ein Parameter t, eine Kurve k (die Leitkurve), ein beliebiger Punkt A0 (Startpunkt), der auf der Kurve k liegt, und ein beliebiger Punkt P0. Sei d der Abstand A0P0.
- Wandert der Punkt A(t) mit A(0) = A0 mit wachsendem t nun entlang der Kurve k, so „folgt“ ihm der Punkt P(t) mit P(0) = P0 in konstantem Abstand d.
- Die Menge aller Punkte, die P(t) durchläuft, bezeichnet man als die Traktrix der Kurve k.
mit
Die Traktrix ist also eine allgemeine Radiodrome
mit der Funktion


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.02. 2022