Sekans hyperbolicus und Kosekans hyperbolicus

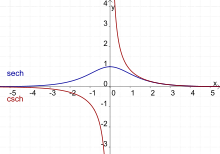
Sekans hyperbolicus (blau) und Kosekans hyperbolicus (rot)

Die Funktionen Kosekans hyperbolicus (csch) und Sekans hyperbolicus (sech) sind Hyperbelfunktionen. Sie ergeben sich als Kehrwert von Sinus hyperbolicus bzw. Kosinus hyperbolicus.

Definitionen

${\displaystyle \begin{align} \operatorname{sech}\ x &= \frac{2}{e^x + e^{-x}} = \frac{1}{\cosh x}\\ \operatorname{csch}\ x &= \frac{2}{e^x - e^{-x}} = \frac{1}{\sinh x} \end{align} }$

Eigenschaften

	Sekans hyperbolicus	Kosekans hyperbolicus
Definitionsbereich	$-\infty <x<+\infty$	$-\infty <x<+\infty \,;\,x\neq 0$
Wertebereich	$0<f(x)\leq 1$	$-\infty <f(x)<+\infty \,;\,f(x)\neq 0$
Periodizität	keine	keine
Monotonie	streng monoton steigend streng monoton fallend	streng monoton fallend streng monoton fallend
Symmetrien	Spiegelsymmetrie zur y-Achse	Punktsymmetrie zum Koordinatenursprung Achsensymmetrie zu y = $-x$
Asymptote	$f(x)\to 0$ für $x \to \pm \infty$	$f(x)\to 0$ für $x \to \pm \infty$
Nullstellen	keine	keine
Sprungstellen	keine	keine
Polstellen	keine
Extrema	Maximum bei x = 0	keine
Wendepunkte	$x=\pm \ln {(1+{\sqrt {2}})}$	keine

Umkehrfunktionen

Die Umkehrfunktion sind die entsprechenden Areafunktionen:

${\displaystyle \begin{align} x &= \operatorname{arsech}\ y\\ x &= \operatorname{arcsch}\ y \end{align} }$

Ableitungen

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sech} \ x&=-\operatorname {sech} \ x\cdot \operatorname {tanh} \ x=-{\frac {\sinh x}{\cosh ^{2}x}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {csch} \ x&=-\operatorname {csch} \ x\cdot \operatorname {coth} \ x=-{\frac {\cosh x}{\sinh ^{2}x}}=-\operatorname {csch} \ x\cdot {\sqrt {1+\operatorname {csch} ^{2}x}}\\\end{aligned}}$

Integrale

${\begin{aligned}\int \operatorname {sech} x\ \mathrm {d} x&=\arctan \left(\sinh x\right)+C\\\int \operatorname {csch} x\ \mathrm {d} x&=\ln \left|\operatorname {tanh} \,{\frac {x}{2}}\right|+C\end{aligned}}$

Reihenentwicklungen

${\displaystyle \begin{align} \operatorname{sech}\ x &= \sum_{k=0}^\infty (-1)^k \frac{(8k + 4)\pi}{(2k+1)^2\pi^2+4 x^2}\\ \operatorname{csch}\ x &= 1/x + \sum_{k=1}^\infty (-1)^k \frac{2 x}{k^2\pi^2+x^2} \end{align} }$

Komplexes Argument

${\begin{aligned}&\operatorname {sech} (x+\mathrm {i} y)={\frac {2\cosh(x)\cos(y)}{\cosh(2x)+\cos(2y)}}+\mathrm {i} {\frac {-2\sinh(x)\sin(y)}{\cosh(2x)+\cos(2y)}}\\&\operatorname {sech} (\mathrm {i} y)=\sec(y)\\&\operatorname {csch} (x+\mathrm {i} y)={\frac {2\sinh(x)\cos(y)}{\cosh(2x)-\cos(2y)}}+\mathrm {i} \;{\frac {-2\cosh(x)\sin(y)}{\cosh(2x)-\cos(2y)}}\\&\operatorname {csch} (\mathrm {i} y)=-\mathrm {i} \csc(y)\end{aligned}}$

Siehe auch

Trigonometrische Funktionen

Basierend auf einem Artikel in:

Wikipedia.de