Areasekans hyperbolicus und Areakosekans hyperbolicus

Areasekans hyperbolicus und Areakosekans hyperbolicus gehören zu den Areafunktionen. Sie sind die Umkehrfunktionen zu Sekans hyperbolicus bzw. Kosekans hyperbolicus. Als Funktionen werden sie $\operatorname {arsech}$ oder seltener $\operatorname {sech} ^{-1}$ bzw. $\operatorname {arcsch} (x)$ und seltener $\operatorname {csch} ^{-1}(x)$ geschrieben.

Definitionen

Man definiert den Areasekans hyperbolicus und Areakosekans hyperbolicus meist über:

$\operatorname {arsech} (x)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)$

$\operatorname {arcsch} (x)=\ln \left({\frac {1+{\sqrt {1+x^{2}}}}{x}}\right)$

Hierbei steht $\ln$ für den natürlichen Logarithmus.

Eigenschaften

Graph der Funktion Areasekans hyperbolicus

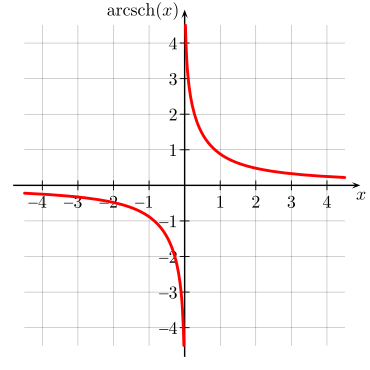
Graph der Funktion Areakosekans hyperbolicus

	Areasecans hyperbolicus	Areakosekans hyperbolicus
Definitionsbereich	$0<x\leq 1$	$-\infty <x<+\infty \,;\,x\neq 0$
Wertebereich	$0\leq f(x)<+\infty$	$-\infty <f(x)<+\infty \,;\,f(x)\neq 0$
Periodizität	keine	keine
Monotonie	streng monoton fallend	$x\neq 0$ streng monoton fallend
Symmetrien	keine	Ungerade Funktion $f(x)=-f(-x)$
Asymptote	$f(x) \to 0$ ; $x\to +1$	$f(x) \to 0$ ; $x\to \pm \infty$
Nullstellen		keine
Sprungstellen	keine	keine
Polstellen
Extrema	keine	keine
Wendepunkte	$x={\frac {1}{2}}{\sqrt {2}}$	keine

Spezielle Werte

Es gilt:

$\operatorname {arcsch} \,2=\ln \Phi$

wobei $\!\ \Phi$ den goldenen Schnitt bezeichnet.

Reihenentwicklungen

${\begin{alignedat}{2}\operatorname {arsech} (x)&=\ln \left({\frac {2}{x}}\right)-\sum _{k=1}^{\infty }{\frac {(2k-1)!!x^{2k}}{(2k)!!2k}}&\qquad \mathrm {f{\ddot {u}}r} \,0<x\leq 1\\\operatorname {arcsch} (x)&=\sum _{k=1}^{\infty }{\frac {P_{k-1}(0)}{k}}x^{k}\\&=\sum _{k=1}^{\infty }{\frac {(-1)^{k}\cdot ({\tfrac {1}{2}})_{k-1}}{(2k-1)(k-1)!}}\,x^{1-2k}\end{alignedat}}$

Dabei ist P_k das -te Legendre-Polynom und $({\tfrac {1}{2}})_{n}$ steht für das Pochhammer-Symbol.

Ableitungen

${\frac {\mathrm {d} }{\mathrm {d} x}}{\rm {arsech}}(x)=-{\frac {1}{x{\sqrt {1-x^{2}}}}}$ .

${\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arcsch} (x)=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}$ .

Integrale

Stammfunktionen des Areasekans hyperbolicus und Areakosekans hyperbolicus sind:

$\int \operatorname {arsech} (x)\,\mathrm {d} x=x\cdot \operatorname {arsech} (x)-\arctan \left({\sqrt {{\frac {1}{x^{2}}}-1}}\right)+C$

$\int \operatorname {arcsch} (x)\,\mathrm {d} x=x\cdot \operatorname {arcsch} (x)+\ln \left(x+x{\sqrt {1+{x}^{-2}}}\right)+C.$

Umrechnung und Beziehungen zu anderen trigonometrischen Funktionen

$\operatorname {arsech} \,(x)=\operatorname {arcosh} \left({\frac {1}{x}}\right)$

$\operatorname {arcsch} \,(x)=\operatorname {arsinh} \left({\frac {1}{x}}\right)$

Siehe auch

Trigonometrische Funktionen

Basierend auf einem Artikel in:

Wikipedia.de