
Pochhammer-Symbol
Das Pochhammer-Symbol ist eine spezielle Funktion, die in der Kombinatorik und in der Theorie der hypergeometrischen Funktionen verwendet wird. Der Name geht auf Leo August Pochhammer zurück.[1]
Definition
Das Pochhammer-Symbol wird über die Gammafunktion definiert:
Aus der Funktionalgleichung der Gammafunktion folgt dann
.
Man hat also eine Identität
mit der steigenden Faktoriellen.
Eigenschaften
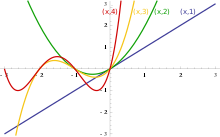
- Das Pochhammer-Symbol ist eine meromorphe Funktion.
- Ist
, so kann
als Polynom in
dargestellt werden. Diese haben eine gemeinsame Nullstelle bei
.
- Zusammenhang zwischen Koeffizienten verschiedener Vorzeichen:
- Divisionsregel:
- Spezielle Werte:
q-Pochhammer-Symbol
Das -Pochhammer-Symbol
ist das
-Analog
des Pochhammer-Symbols und spielt eine Rolle in der Kombinatorik bei
-Analoga
klassischer Formeln, wobei, angeregt durch den Grenzübergang
,
das -Analogon
natürlicher Zahlen über
definiert wird.
Das -Pochhammer-Symbol
wird über die formale
Potenzreihe in der Variablen
definiert:
mit
.
Sie werden auch -Reihen
genannt und
als
abgekürzt, z.B.
.
Es lässt sich auch zu einem unendlichen Produkt erweitern:
Der Spezialfall
ist das Eulersche Produkt, das eine Rolle in der Theorie der Partitionsfunktion spielt.
Denn die Maclaurinsche Reihe für den Kehrwert des Eulerschen Produkts trägt die Partitionszahlen als Koeffizienten:
Dabei steht P(n) für die n-te Partitionszahl.
Die Maclaurinsche Reihe für das Eulersche Produkt selbst hat an allen Summanden die Fünfeckszahlen und Kartenhauszahlen als Exponenten:
Dabei steht F(n) für die n-te Fünfeckszahl und K(n) für die n-te Kartenhauszahl:
Diese Tatsache basiert auf dem Pentagonalzahlensatz von Leonhard Euler.
Das Eulersche Produkt kann auch mit der Jacobischen Thetafunktion ausgedrückt werden:
Der Mathematiker Srinivasa Ramanujan entdeckte folgende Beziehung zu den Thetafunktionen:
Sie finden sich in seinem Aufsatz Modular Equations and Approximations to π.
Mit dem Pochhammer-Symbol kann auch die Rogers-Ramanujan-Kettenbruchfunktion R(x) dargestellt werden:
In der ersten Zeile der Gleichungskette werden die Rogers-Ramanujan-Identitäten repräsentiert.
Dabei wurden für eine kompaktere Darstellung die Abkürzungen
verwendet und die Thetafunktionen:
Anmerkung
- ↑
L. Pochhammer: Ueber die Differentialgleichung der allgemeineren
hypergeometrischen Reihe mit zwei endlichen singulären Punkten.
Journal für die reine und angewandte Mathematik, Band 102, S. 76–159, 1888;
insbesondere S. 80–81. Pochhammer benutzt die Bezeichnung
für den Binomialkoeffizienten,
für die fallende Faktorielle und
für die steigende Faktorielle.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.01. 2022