Partitionsfunktion

Die Partitionsfunktionen geben die Anzahl der Möglichkeiten an, positive, ganze Zahlen in positive, ganze Summanden zu zerlegen. Üblicherweise betrachtet man die Zerlegungen ohne Berücksichtigung der Reihenfolge. Jede solche Zerlegung wird in der Kombinatorik als (ungeordnete) Zahlpartition bezeichnet. Die Bestimmung aller Zahlpartitionen für eine bestimmte (große) natürliche Zahl ist ein wichtiges Problem sowohl in der theoretischen als auch der praktischen Informatik.

Die Partitionsfunktion ohne Nebenbedingungen (Anzahl der ungeordneten Zahlpartitionen von ) wird als P(n) , manchmal auch als p(n) notiert und ist Folge A000041 in OEIS. Es gibt eine Reihe von Funktionen, bei denen an die Summanden zusätzliche Bedingungen gestellt werden, zum Beispiel dass jeder Summand nur einmal vorkommen darf (strikte Zahlpartitionen), diese Variante wird ebenfalls Partitionsfunktion, manchmal auch strikte Partitionsfunktion genannt, als Q(n) oder q(n) notiert und ist Folge A000009 in OEIS.

Partitionsfunktion P(n) in halblogarithmischer Darstellung

Mit einer aus der Partitionsfunktion P(n) abgeleiteten zahlentheoretischen Funktion kann die Anzahl der Isomorphietypen für die endlichen abelschen Gruppen angegeben werden.

Eigenschaften von P(n)

Beispielwerte

Beispielwerte von P(n) und zugehörige Zahlpartitionen
n	P(n)	Zahlpartitionen
0	1	() leere Partition/leere Summe
1	1	(1)
2	2	(1+1), (2)
3	3	(1+1+1), (1+2), (3)
4	5	(1+1+1+1), (1+1+2), (2+2), (1+3), (4)
5	7	(1+1+1+1+1), (1+1+1+2), (1+2+2), (1+1+3), (2+3), (1+4), (5)
6	11	(1+1+1+1+1+1), (1+1+1+1+2), (1+1+2+2), (2+2+2), (1+1+1+3), (1+2+3), (3+3), (1+1+4), (2+4), (1+5), (6)

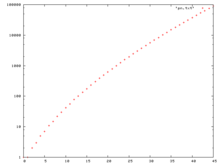
Die Werte steigen danach schnell an:

${\begin{array}{lcr|lcr|lcr}P(7)&=&15&P(45)&=&89\,134\\P(8)&=&22&P(100)&=&190\,569\,292&\\P(9)&=&30&P(200)&\approx &3,973\cdot 10^{{12}}\\P(10)&=&42&P(1000)&\approx &2,406\cdot 10^{{31}}\end{array}}$

Rekursive Darstellung

Beispielwerte von P(n,k)
P(n,k)		1	2	3	4	5	6	7	8	9	10
P(n,k)		k
n	1	1
	2	1	1
	3	1	1	1
	4	1	2	1	1
	5	1	2	2	1	1
	6	1	3	3	2	1	1
	7	1	3	4	3	2	1	1
	8	1	4	5	5	3	2	1	1
	9	1	4	7	6	5	3	2	1	1
	10	1	5	8	9	7	5	3	2	1	1

Bezeichnet P(n,k) die Anzahl der Möglichkeiten, die positive, ganze Zahl in genau positive, ganze Summanden zu zerlegen, dann gilt

$P(n)=\sum _{{i=1}}^{n}P(n,i)$ ,

wobei sich die Zahlen P(n,k) rekursiv über P(n,1)=1 und P(n,n)=1 sowie

$P(n+k,k)=\sum _{{j=1}}^{k}P(n,j)$

oder direkt durch

ermitteln lassen.

Asymptotisches Verhalten

Relativer Fehler der Approximationsfunktion
	5	10	100	250	500
${\frac {E(n)-P(n)}{P(n)}}$ in %	27,7	14,5	4,57	2,86	2,01

Für große Werte von gibt die Formel von Godfrey Harold Hardy und S. Ramanujan

$P(n)\sim E(n)={\frac {\exp \left(\pi {\sqrt {2n/3}}\right)}{4n{\sqrt {3}}}}$

einen guten Näherungswert für P(n) . Insbesondere bedeutet dies, dass die Anzahl der Dezimalstellen von P(n) etwa proportional zur Quadratwurzel aus ist: P(100) hat 9 Stellen ( ${\sqrt {100}}=10$ ), P(1000) hat 32 Stellen ( ${\sqrt {1000}}\approx 31{,}6$ ).

P(4n) hat etwa doppelt so viele Stellen wie P(n) .

Erzeugende Funktion

Eine einfache erzeugende Funktion für die Partitionsfunktion gewinnt man aus der multiplikativ Inversen von Eulers Funktion

$\sum _{{n=0}}^{\infty }P(n)x^{n}=\prod _{{k=1}}^{\infty }{\frac {1}{1-x^{k}}}$

Man erhält

$f(x)={\frac {1}{\prod _{{k=1}}^{\infty }(1-x^{k})}}=1+1x+2x^{2}+3x^{3}+5x^{4}+...$

d.h. dass die Koeffizienten der Reihendarstellung von f(x) den Werten von P(n) entsprechen.

Zusammenhang mit den Pentagonalzahlen

Die Koeffizienten c(n) von Eulers Funktion (Euler-Produkt)

$\prod _{{k=1}}^{\infty }(1-x^{k})\;=\sum _{{m=-\infty }}^{\infty }(-1)^{m}\cdot x^{{{\frac {m(3m-1)}{2}}}}=\sum _{{n=0}}^{\infty }c(n)\cdot x^{n}$

lassen sich mit dem Pentagonalzahlensatz von Leonhard Euler einfach explizit berechnen. Die Folge c(n) ist Folge A010815 in OEIS und es gilt stets $c(n)\in \{-1,0,1\}.$

Aus der Tatsache, dass Eulers Funktion multiplikativ invers zur erzeugenden Funktion der Partitionsfunktion ist, folgt, dass für die diskrete Faltung $c\ast P$ und $n\in \mathbb {N} _{0}$ gilt

$(c\ast P)(n)=\sum _{{r\in \mathbb{Z } }}c(r)\cdot P(n-r)=\sum _{{r=0}}^{n}P(r)\cdot c(n-r)={\begin{cases}1\;(n=0)\\0\;(n\neq 0).\end{cases}}$

Die Summation muss nur über $r\in \{0,1,\ldots n\}$ erstreckt werden, da beide Folgen als Koeffizientenfolgen ihrer jeweiligen Funktion an negativen Stellen gleich Null sind.

Rekursionsformel aus dem Pentagonalzahlensatz

Aus der im vorigen Unterabschnitt angegebenen Faltungsbeziehung zu den Koeffizienten c(n) folgt für $n\in \mathbb{N} \setminus \{0\}$ die Rekursionsformel

$P(n)=-\sum _{{r=1}}^{{n}}c(r)\cdot P(n-r)=P(n-1)+P(n-2)-P(n-5)-P(n-7)+\cdots$

für die Partitionsfunktion.

Berechnung mit analytischer Zahlentheorie

Eine Möglichkeit zur direkten Berechnung liefert die aus der erzeugenden Funktion hergeleitete Formel

$P(n)={\frac {1}{\pi {\sqrt {2}}}}\sum _{{k=1}}^{\infty }A_{k}(n)\;{\sqrt {k}}\;{\frac {{\mathrm d}}{{\mathrm d}n}}\left({\frac {\sinh \left({\frac {\pi }{k}}{\sqrt {{\frac {2}{3}}\left(n-{\frac {1}{24}}\right)}}\right)}{{\sqrt {n-{\frac {1}{24}}}}}}\right)$

mit

$A_{k}(n)=\!\!\!\!\sum _{{0\leq m<k \atop \operatorname {ggT}(m,k)=1}}\!\!\!\!\exp \left\{{\frac {\pi i}{k}}\left[s(m,k)-2nm\right]\right\}.$

und

$s(m,k)=\sum _{{j=1}}^{{k-1}}j\left({\frac {mj}{k}}-\left\lfloor {\frac {mj}{k}}\right\rfloor -{\frac {1}{2}}\right)$

die Hans Rademacher, aufbauend auf Erkenntnissen von S. Ramanujan und Godfrey Harold Hardy, fand.

Berechnung mit algebraischer Zahlentheorie

Eine algebraische, geschlossene Form von P(n) , die ohne unendliche Reihenentwicklung auskommt, wurde 2011 von Jan Hendrik Bruinier und Ken Ono veröffentlicht. Genauer gesagt geben Bruinier und Ono eine Funktion an, so dass sich für jede natürliche Zahl eine endliche Anzahl algebraischer Zahlen $\alpha _{1},\alpha _{2},\ldots ,\alpha _{m}$ mit

$P(n)={\frac {1}{24n-1}}\left(Q(\alpha _{1})+Q(\alpha _{2})+\ldots +Q(\alpha _{m})\right)$

finden lassen. Darüber hinaus gilt, dass auch alle Werte $Q(\alpha _{i})$ algebraisch sind.

Dieses theoretische Ergebnis führt nur in Spezialfällen (z.B. über daraus ableitbare Kongruenzen) zu einer schnelleren Berechnung der Partitionsfunktion.

Kongruenzen

		Kongruenzen
1	1
2	2
3	3
4	5	mod 5
5	7	mod 7
6	11	mod 11
7	15
8	22
9	30	mod 5
10	42
11	56
12	77	mod 7
13	101
14	135	mod 5
15	176
16	231
17	297	mod 11
18	385
19	490	mod 5 und 7
20	627

Ramanujan entdeckte bei seinen Studien eine Gesetzmäßigkeit. Beginnt man mit der 4 und springt um 5, so erhält man immer Vielfache der Sprungzahl 5 als Zerlegungszahlen. Beginnt man bei der 6 und springt um 11, so erhält man Vielfache von 11. Ramanujan entdeckte weitere derartige Beziehungen, auch Kongruenzen genannt, als er die Potenzen der Primzahlen 5, 7 und 11 sowie deren Produkte als Sprungzahlen untersuchte. Der amerikanische Zahlentheoretiker Ken Ono konnte zeigen, dass es für alle Primzahlen größer 3 Kongruenzen gibt. Ob dies für die beiden kleinsten Primzahlen, die 2 und 3, und deren Vielfache ebenso gilt, konnte Ono nicht nachweisen. Folgende Kongruenzen gehen auf Ramanujan zurück:

${\begin{aligned}P(5k+4)&\equiv 0\mod 5\\P(7k+5)&\equiv 0\mod 7\\P(11k+6)&\equiv 0\mod {11}\end{aligned}}$

A. O. L. Atkin fand folgende Kongruenz:

$P(17303k+237)\equiv 0\mod {13}$

Ferrers-Diagramme

Die Zahlpartition 6+4+3+1=14 kann durch folgendes Diagramm, das als Ferrers-Diagramm bezeichnet wird, dargestellt werden. Diese Diagramme wurden zu Ehren von Norman Macleod Ferrers benannt.

6 + 4 + 3 + 1

Die 14 Kreise werden in 4 Spalten für die 4 Summanden der Partition aufgereiht, wobei die Spalten von links nach rechts nie höher werden. Es wird auch häufig die umgekehrte Konvention verwendet, bei der die Säulen von Kreisen auf der Grundlinie stehen und von links nach rechts nie niedriger werden. Die 5 Partitionen von 4 sind nachfolgend als Ferrers-Diagramme dargestellt:


4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

Konjugierte Partition

Wenn wir das Diagramm der Partition 6+4+3+1=14 an seiner Hauptdiagonale spiegeln, erhalten wir eine andere Partition von 14:

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

Indem wir so Reihen in Spalten verwandeln, erhalten wir die Partition 4+3+3+2+1+1=14 . Sie heißt die zu 6+4+3+1=14 konjugierte Partition. Unter den Partitionen von 4 sind 1+1+1+1=4 und 4=4 ; 3+1 und 2+1+1 jeweils konjugiert zueinander. Besonders interessant sind Partitionen wie 3+2+1=6 , die zu sich selbst konjugiert sind, deren Ferrers-Diagramm also achsensymmetrisch zu seiner Hauptdiagonalen ist.

Die Anzahl der zu sich selbst konjugierten Partitionen von ist gleich der Anzahl der Partitionen von in verschiedene, ungerade Summanden.

Beweisidee: Die entscheidende Beobachtung ist, dass jede Spalte im Ferrers-Diagramm, die eine ungerade Anzahl von Kreisen enthält, in der Mitte „gefaltet“ werden kann und so einen Teil eines symmetrischen Diagramms ergibt:

↔

Daraus gewinnt man, wie im folgenden Beispiel gezeigt, eine bijektive Abbildung der Partitionen mit verschiedenen, ungeraden Summanden auf die Partitionen, die zu sich selbst konjugiert sind:

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2

Mit ähnlichen Methoden können zum Beispiel die folgenden Aussagen bewiesen werden: Die Anzahl der Partitionen von mit höchstens Summanden ist gleich

der Anzahl der Partitionen von , bei denen kein Summand größer als ist.
der Anzahl der Partitionen von mit genau Summanden.

Formalisierung

Die Ferrers-Diagramme sind ein intuitives Hilfsmittel, mit denen sich Zusammenhänge zwischen ungeordneten Partitionen anschaulich erkennen und nachvollziehen lassen. Für die Erzeugung mit Computern und kompakte Speicherung sind sie ungeeignet, daher spielen auch „formalisierte“ Repräsentationen für diese Diagramme eine wichtige Rolle:

Eine Zahlpartition von $n\in \mathbb {N}$ („Diagramm der Ordnung “) ist ein -Tupel („Anzahl der Spalten=Columns“) $\pi =\operatorname {(i_{k})}_{{k=1}}^{C}\in \left(\mathbb{N} \setminus \{0\}\right)^{C}$ mit der Eigenschaft $\sum \nolimits _{{k=1}}^{C}i_{k}=n$ , heißt ihre Spaltenzahl. (Um hier auch die „leere“ Partition $()=\operatorname {()}_{{k=1}}^{0}$ mitzuerfassen, muss man für setzen $\left(\mathbb{N} \setminus \{0\}\right)^{0}:=\{()\}$ , es ist dann die leere Summe und ergibt immer 0.)
Die Zahl $R=R(\pi )=\max(0,\max\{i_{k}:1\leq k\leq C\})$ heißt die Zeilenzahl (=„Rows“) von $\pi =\operatorname {(i_{k})}_{{k=1}}^{C}.$
Eine Zahlpartition $\pi =\operatorname {(i_{k})}_{{k=1}}^{C}$ heißt „gültig“, wenn für $1\leq k<C$ stets $i_{k}\geq i_{{k+1}}$ gilt, für gültige Partitionen mit ist $R(\pi )=i_{1}$ .
Eine Zahlpartition $\pi =\operatorname {(i_{k})}_{{k=1}}^{C}$ heißt „strikt“, wenn für $1\leq k<C$ stets $i_{k}>i_{{k+1}}$ gilt. Strikte Partitionen sind immer gültig.
Die konjugierte Partition einer gültigen Partition $\pi =\operatorname {(i_{k})}_{{k=1}}^{C}$ ist definiert durch $\overline {\pi }=\operatorname {\left(\max\{k:\,{i_{k}}+1-r>0\land 1\leq k\leq C\}\right)}_{{r=1}}^{{R(\pi )}}$ . Sie ist gültig.

Alternativ und näher an der grafischen Darstellung der Ferrers-Diagramme kann man jede Partition als $R\times C$ -Matrix $(a_{{jk}})$ mit Einträgen aus $\{0,1\}$ darstellen, wobei $a_{{jk}}=1$ bedeutet, dass sich im Ferrers-Diagramm in der Reihe in Spalte ein Kreis befindet, $a_{{jk}}=0$ , dass dort kein Kreis ist. Die Konjugierte einer Partition hat dann als Matrix die transponierte Matrix der ursprünglichen Partition.

Varianten

Partitionen mit vorgegebenem kleinsten Summanden, p(k,n)

Bei einer Abwandlung der Partitionsfunktion wird verlangt, dass der kleinste Summand in der Zahlpartition größer oder gleich ist. Die Anzahl solcher Partitionen wird als p(k,n) notiert. Die „normale“ Partitionsfunktion ist somit P(n)=p(1,n). Diese Abwandlung p(k,n) ist Folge A026807 in OEIS.

Beispielwerte für p(k,n)

Beispielwerte von p(k,n)
p(k,n)		1	2	3	4	5	6	7	8	9	10
p(k,n)		k
n	1	1
	2	2	1
	3	3	1	1
	4	5	2	1	1
	5	7	2	1	1	1
	6	11	4	2	1	1	1
	7	15	4	2	1	1	1	1
	8	22	7	3	2	1	1	1	1
	9	30	8	4	2	1	1	1	1	1
	10	42	12	5	3	2	1	1	1	1	1

Zu den Werten von p(k,n) für kleine Zahlen siehe auch die zweite Tabelle rechts. Einzelwerte sind:

${\begin{alignedat}{4}p(1,4)&=5,&p(2,8)&=7,&p(3,12)&=9,\\p(4,16)&=11,\quad &p(5,20)&=13,\quad &p(6,24)&=16.\end{alignedat}}$

Rekursionsformel für p(k,n) und P(n)

Es gilt

$p(k,n)=1+\sum _{{j=k}}^{{\lfloor {\frac {n}{2}}\rfloor }}p(j,n-j);\;p(n,n)=1$

wobei $\lfloor n\rfloor$ die Gaußklammer ist. Mit dieser Rekursionsformel lassen sich alle Werte von p(k,n) und damit auch für P(n)=p(1,n) berechnen. Man beachte aber, dass bei der Rekursionsformel für die Berechnung von p(1,N) alle Werte von p(k,n) für $1\leq k<\lfloor {\frac {N}{2}}\rfloor ;\;1<n<N$ bekannt sein oder mit berechnet werden müssen.

Geordnete Zahlpartitionen

Betrachtet man die Summanden in einer Zahlpartition als geordnete Menge, berücksichtigt also die Reihenfolge in der Summe, dann spricht man von einer geordneten Zahlpartition. Hier werden die folgenden Anzahlfunktionen betrachtet, für die kein Formelzeichen allgemein verbreitet ist.

ist die Anzahl der Darstellungen von als Summe von genau positiven ganzen Zahlen mit Berücksichtigung der Reihenfolge der Summanden, also die Anzahl der Lösungen $(i_{1},i_{2},\ldots i_{k})\in \left(\mathbb{N} \setminus \{0\}\right)^{k}$ der Gleichung $i_{1}+i_{2}+\cdots +i_{k}=n.$

Es gilt $g(k,n)={\binom {n-1}{k-1}}$ .
Die Anzahl lässt sich geometrisch deuten als Zahl der Punkte mit positiven, ganzzahligen Koordinaten auf der Hyperebene mit der Gleichung $x_{1}+x_{2}+\cdots +x_{k}=n$ im -dimensionalen reellen affinen Punktraum.
Die Folge $g(1,1),g(1,2),g(2,2),g(1,3),g(2,3),g(3,3),g(1,4),\ldots$ ist die Folge der Zahlen im pascalschen Dreieck, den Reihen nach gelesen, Folge A007318 in OEIS.

ist die Anzahl der Darstellungen von als Summe von höchstens positiven ganzen Zahlen mit Berücksichtigung der Reihenfolge der Summanden. Sie ist Folge A000079 in OEIS und es gilt

$G(n)=\sum _{{j=1}}^{n}g(j,n)$ ,
die Rekursionsformel $G(n)=1+\sum _{{i_{1}=1}}^{{n-1}}G(n-i_{1}),\,n\geq 1$ und
$G(n)=2^{{n-1}},n\geq 1$ , was sich leicht mit vollständiger Induktion aus der Rekursionsformel beweisen lässt.

Offenbar liefert die leicht zu berechnende Funktion G(n) eine (sehr grobe) obere Schranke für die Partitionsfunktion:

$P(n)<G(n)=2^{{n-1}},\ n\geq 3.$

Strikte Partitionen und verwandte Nebenbedingungen

Die Zahlpartitionen von , die aus lauter ungeraden Summanden bestehen, lassen sich bijektiv abbilden auf die strikten Zahlpartitionen, das sind die Zahlpartitionen mit lauter unterschiedlichen Summanden. Diese Tatsache wurde bereits 1748 von Euler nachgewiesen. Sie ist ein Spezialfall des Satzes von Glaisher der nach James Whitbread Lee Glaisher benannt ist:

Die Anzahl der Partitionen von , bei denen kein Summand durch $d\in \mathbb{N} \setminus \{0,1\}$ teilbar ist, gleicht der Anzahl der Partitionen von , in denen keine übereinstimmenden Summanden vorkommen.

Damit verwandt ist die folgende Aussage, die nach Leonard James Rogers als Satz von Rogers benannt ist:

Die Anzahl der Partitionen von , deren Summanden sich um 2 oder mehr unterscheiden, ist der Anzahl der Partitionen von gleich, bei der alle Summanden bei Division durch 5 den Rest 1 oder 4 lassen.

Die Aussage ist Teil der Rogers-Ramanujan-Identitäten.

Mathematische Anwendungen

Konjugationsklassen der symmetrischen Gruppe

Die Anzahl der Konjugationsklassen in der symmetrischen Gruppe $S_{n}$ ist gleich dem Wert P(n) der Partitionsfunktion, denn jede Konjugationsklasse entspricht genau einem Zykeltyp von Permutationen mit einer bestimmten Struktur der Darstellung in disjunkter Zyklenschreibweise.

Beispiele

Die Permutation gehört als Element der $S_{9}$ zu der Zahlpartition der Zahl 9, als Element der $S_{{12}}$ zur Zahlpartition von 12. Man beachte, dass Fixelemente der Permutation, die in der Zyklenschreibweise (als „Einerzyklen“) fast immer fortgelassen werden, in der Zahlpartition als Summanden 1 auftauchen. Jedes Element der $S_{{12}}$ , das in der disjunkten Zyklenschreibweise aus einem Dreier- und einem Viererzyklus besteht, ist in $S_{{12}}$ zu dem oben genannten Element konjugiert, es gibt in diesem Fall ${\binom {12}{4}}\cdot {\binom {8}{3}}\cdot 3!\cdot 2!=332\,640$ solche Permutationen.
Die Permutation gehört als Element der $S_{{12}}$ zur Zahlpartition von 12. Sie gehört in $S_{{12}}$ zu einer Konjugationsklasse, die ${\binom {12}{3}}\cdot {\binom {9}{3}}\cdot {\binom {6}{2}}\cdot {\frac {2!\cdot 2!}{2!}}=554\,400$ Permutationen enthält.

Zahlpartition und endliche Mengenpartition

Jede Äquivalenzrelation auf einer endlichen Menge mit Elementen bestimmt eine Mengenpartition von . In der Kombinatorik wird ohne Einschränkung der Allgemeinheit $M=\{1,2,\ldots n\}$ angenommen. Zu jeder Zahlpartition von gehört eine nicht leere Menge von isomorphen Äquivalenzklasseneinteilungen der Menge . Die Anzahl der Zahlpartitionen von ist daher kleiner gleich der Anzahl der Mengenpartitionen von , für $n\geq 3$ echt kleiner:

Beispiele

	0	1	2	3	4	5	6	7	8	9	10	11
Anzahl der Zahlpartitionen	1	1	2	3	5	7	11	15	22	30	42	56
Anzahl der Mengenpartitionen $B_{n}$	1	1	2	5	15	52	203	877	4140	21147	115975	678570

Zu der Zahlpartion von 3 gehören die 3 Mengenpartitionen $\{\{1,2\},\{3\}\};\{\{1,3\},\{2\}\};\{\{2,3\},\{1\}\}$ .
Zu den Zahlpartitionen und von 5 gehören je ${\binom {5}{3}}=10$ Mengenpartitionen, zu den Zahlpartitionen und je genau eine Mengenpartion.

Endliche abelsche p-Gruppen und abelsche Gruppen

Ist eine positive Primzahl, dann ist für $n\in \mathbb {N}$ jede Gruppe mit der Gruppenordnung $p^{n}$ eine p-Gruppe. Die Anzahl der (Isomorphieklassen von) abelschen Gruppen mit $p^{n}$ Gruppenelementen ist – unabhängig von der Primzahl – gleich dem Wert P(n) der Partitionsfunktion, denn jede solche Gruppe ist nach dem Hauptsatz über endlich erzeugte abelsche Gruppen isomorph zu einem direkten Produkt $G\cong \mathbb{Z } /p^{{k_{1}}}\mathbb{Z } \times \mathbb{Z } /p^{{k_{2}}}\mathbb{Z } \times \cdots \times \mathbb{Z } /p^{{k_{r}}}\mathbb{Z }$ mit $p^{n}=p^{{k_{1}}}\cdot p^{{k_{2}}}\cdot \cdots \cdot p^{{k_{r}}}$ und also $n=k_{1}+k_{2}+\cdots +k_{r}$ . Da die Isomorphieklasse nicht von der Reihenfolge der Faktoren im direkten Produkt abhängt, entspricht jede Isomorphieklasse von abelschen Gruppen mit $p^{n}$ Elementen umkehrbar eindeutig einer Zahlpartition von .

Zum Beispiel gibt es bis auf Isomorphie jeweils genau P(5)=7 abelsche Gruppen mit $32=2^{5},243=3^{5},3125=5^{5}$ Elementen.

Anwendungsbeispiele

Wie viele Isomorphietypen von abelschen Gruppen mit genau 70000 Elementen gibt es? Jede solche Gruppe ist, wieder nach dem Hauptsatz ein direktes Produkt ihrer abelschen p-Sylowgruppen zu den Primzahlen 2, 5 und 7. Es ist $70000=2^{4}\cdot 5^{4}\cdot 7^{1}$ , also existieren $P(4)\cdot P(4)\cdot P(1)=5\cdot 5\cdot 1=25\,$ „wesentlich verschiedene“ abelsche Gruppen mit 70000 Elementen.
Wie viele Isomorphietypen von abelschen Gruppen mit 7200 Elementen gibt es, die ein Element der Ordnung 180 enthalten? Es ist $180=2^{2}\cdot 3^{2}\cdot 5^{1};7200=2^{5}\cdot 3^{2}\cdot 5^{2}$ . Von den abelschen 2-Gruppen und 3-Gruppen kommen nur solche in Betracht, die zu einer Partition von 5 bzw. 2 gehören, die einen Summanden größer oder gleich 2 enthält, damit fällt jeweils eine Zahlpartition (Summe von Einsen) weg. Es gibt also $(P(5)-1)\cdot (P(2)-1)\cdot P(2)=6\cdot 1\cdot 2=12$ solche Gruppen.
Ist nun zusätzlich zu den Informationen des vorigen Beispiels bekannt, dass kein Element eine größere Ordnung als 180 hat, so kommen nur noch 2 Arten von 2-Sylowgruppen und eine Art 5-Sylowgruppe in Betracht und es gibt genau 2 Isomorphietypen von Gruppen mit diesen Eigenschaften.

Anzahlfunktion von Isomorphietypen endlicher abelscher Gruppen

Der Hauptsatz über die endlich erzeugten abelschen Gruppen erlaubt es, die Anzahl a(n) der Isomorphietypen endlicher abelscher Gruppen mit Elementen durch die Partitionsfunktion auszudrücken:

Zu jeder natürlichen Zahl $n\in \mathbb{N} \setminus \{0\}$ mit der Primfaktorzerlegung $n={p_{1}}^{{r_{1}}}\cdot {p_{2}}^{{r_{2}}}\cdots {p_{k}}^{{r_{k}}}$ existieren genau $a(n)=P(r_{1})\cdot P(r_{2})\cdots P(r_{k})$ Isomorphietypen von abelschen Gruppen mit Elementen.
Die Folge ist Folge A000688 in OEIS, sie ist eine multiplikative zahlentheoretische Funktion von und als solche durch ihre Werte für Primzahlpotenzen vollständig bestimmt.
Die der Anzahlfunktion zugeordnete (formale) Dirichletreihe ist

$A(s)=\sum _{{n=1}}^{{\infty }}{\frac {a(n)}{n^{s}}},\,$ mit $s=\sigma +it\in {\mathbb {C}},\,$ ihr Eulerprodukt lautet $A(s)=\prod _{{p\ {{\mathrm {prim}}}}}\sum _{{r=0}}^{{\infty }}{\frac {P(r)}{p^{{rs}}}}.$

Die Anzahlfunktion gibt für $n\geq 2$ zugleich die Anzahl der durch die Teilbarkeitsrelation geordneten Ketten $(t_{1},t_{2},\ldots ,t_{r})\in \left\lbrace \left(\mathbb{N} \setminus \{0,1\}\right)^{r}:\;t_{1}|t_{2}|\cdots |t_{r}\right\rbrace$ an, deren Produkt gleich ist $(t_{1}\cdot t_{2}\cdot \cdots t_{r}=n).$

Basierend auf einem Artikel in:

Wikipedia.de