
Kettenlinie (Mathematik)

Eine Kettenlinie (auch Seilkurve, Katenoide oder Kettenkurve, englisch catenary oder funicular curve) ist eine mathematische Kurve, die den Durchhang einer an ihren Enden aufgehängten Kette unter dem Einfluss der Schwerkraft beschreibt. Es handelt sich um eine elementare mathematische Funktion, den Cosinus hyperbolicus, kurz cosh.
Mathematische Beschreibung
Die Berechnung der Kettenlinie ist ein klassisches Problem der Variationsrechnung. Man denkt sich ein Seil von gewisser Masse und Länge, das an seinen Enden aufgehängt ist. Die Seilkurve ist das Ergebnis der kleinst möglichen potentiellen Energie des Seils. Das versucht man rechnerisch nachzuvollziehen.
Dazu benötigt man den mathematischen Ausdruck für die potentielle Energie. Er
ist eine Verfeinerung des bekannten „Gewicht mal Höhe“ .
Die Verfeinerung besteht darin, dass die Energie für „alle Teile“ des Seils
getrennt ausgewertet und zum Schluss aufsummiert wird. Das ist notwendig, weil
die Teile des Seils sich auf unterschiedlichen Höhen befinden. Die gedankliche
Zerlegung des Seils in immer kleinere Teile macht aus der Summe ein Integral.
Die Höhe
aus
wird durch die gesuchte Funktion
ersetzt, die Masse
durch die Masse
des Seilstücks über dem Intervall
;
nach Pythagoras ist dies:
wobei
die Masse je Meter ist. Wenn das Seil an den Stellen
,
aufgehängt ist, ergibt sich demnach die Energie („Gewicht mal Höhe“) als
Eine ähnliche Überlegung führt auf den Ausdruck für die Länge des Seils:
Die Energie ist zu minimieren, die Länge ist jedoch vorgegeben. Man bringt
dies unter einen Hut durch einen Lagrange-Multiplikator
,
das heißt, man minimiert nun den Ausdruck
Die Variation ergibt die Differentialgleichung (Euler-Lagrange-Gleichung):
Interessanterweise sind in diesem Schritt sowohl die Massengröße
als auch die Schwerebeschleunigung
herausgefallen. Ein schweres Seil nimmt somit dieselbe Form an wie ein leichtes,
und auf dem Mond ergibt sich trotz anderer Fallbeschleunigung dieselbe Form wie
auf der Erde.
Die Lösungen der Gleichung sind die Funktionen
Es handelt sich um vergrößerte und verschobene Cosinus-hyperbolicus-Funktionen.
ist der Krümmungsradius
im Scheitelpunkt (siehe Abbildung) und zugleich der Vergrößerungsfaktor.
ist die Verschiebung in
-Richtung,
die Verschiebung in
-Richtung.
Die konkrete Form, die das Seil letztendlich annimmt, errechnet man, indem
man ,
und
so anpasst, dass die Kurve durch die Aufhängepunkte geht und die vorgegebene
Länge
hat.
Beispiel
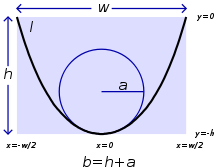
Als Beispiel sei ein zwischen zwei Pfosten (Abstand )
aufgehängtes Seil der Länge
gegeben (siehe Abbildung).
Die Pfosten sind gleich hoch und befinden sich bei
und
,
es gilt also
.
Um den Krümmungsradius
zu berechnen, schreiben wir die Seillänge
als Funktion von
:
.
Diese Beziehung legt
in Abhängigkeit von
und
eindeutig fest. Da man keinen geschlossenen Ausdruck für
angeben kann, muss der Wert mit einem numerischen
Verfahren zur Lösung nichtlinearer Gleichungen approximativ berechnet
werden.
Sind jedoch
und
gegeben, können
und
wie folgt geschlossen dargestellt werden.
Wird das Quadrat aus der Gleichung (oben)vom Quadrat aus der (unten erwähnten) Gleichung
subtrahiert, dann ergibt die mit der Differenz entstehende Gleichung
, woraus
wegen
eliminiert und nach
umgestellt werden kann.
Einsetzen diesesin
und Umformungen ergeben den gesuchten Ausdruck für den Abstand in geschlossener Form z.B.
oder
.
Zuletzt liest man aus der Abbildung die Bedingung
ab, aus der man
erhält. Des Weiteren gelten die Beziehungen
wobei
der „Durchhang“ ist.
Die potentielle Energie dieses Systems beträgt
.
Genauer ist dies die Energiedifferenz gegenüber dem Fall, dass sich das Seil
komplett auf der Höhe der Aufhängepunkte ()
befindet.
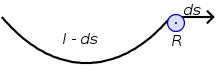
Mit Hilfe der Energie kann man die Kraft
in den Aufhängepunkten berechnen. Hierzu stellt man sich vor, dass das Seil in
einem Aufhängepunkt über eine Umlenkrolle
läuft, die die Kraft in horizontale Richtung umlenkt. Um das Seil wie abgebildet
um eine sehr kleine Strecke
hinauszuziehen, muss man die Energie
aufwenden. Diese kann man berechnen und erhält so die Kraft
.
Zur Berechnung von
vergleicht man die Energie des ursprünglichen Seils mit der des um
verkürzten Seiles. Das Ergebnis ist überraschend einfach, nämlich
mit .
Dieselbe Formel kann man auch auf Teilstücke des Seils anwenden. Da die
Teilstücke alle denselben Krümmungsradius
haben, aber für kleine Teilstücke (unten im Tal) der Durchhang
vernachlässigbar wird, besteht im Tal des Seiles die Seilspannung
.
Stellt man die Pfosten nah beisammen, dann dominiert der Durchhang ,
der dann recht genau die halbe Seillänge ist. Die Kraft ist dann erwartungsgemäß
die halbe Gewichtskraft des Seiles,
(man beachte, dass zwei Aufhängepunkte sich die Last teilen).
Die Formel zeigt auch, wie die Kraft bei zunehmender Seilspannung die halbe
Gewichtskraft um den Faktor
übersteigt. Der Faktor ist praktisch 1 für sehr kleine Krümmungsradien
,
aber ungefähr
oder auch
für sehr große Krümmungsradien.
Im Alltag beträgt der Faktor etwa 2 bis 4. Im Aufhängepunkt wirkt dann das ganze oder doppelte Gewicht des Seiles.
Beziehungen zu anderen Funktionen
-1;_x^2.png)
m(0)=1/2, c(0)=2: Der unbestimmte Ausdruck 0/0 ist in diesem Fall 1/2 bzw. 2.
Parabel
Joachim Junge wies 1639 nach, dass die Kettenlinie keine Parabel ist. Gottfried Leibniz, Christiaan Huygens und Johann I Bernoulli fanden 1690/91 heraus, wie die Kettenkurve zu bilden ist. Die Parabel stellt sich ein bei einer gleichmäßig über die Spannweite x verteilten Streckenlast, z.B. einer Hängebrücke, bei der das Gewicht der Seile gegenüber dem der Fahrbahn vernachlässigt werden kann. Die Abbildung rechts vergleicht den Kurvenverlauf einer Kettenlinie (rot) mit einer Normalparabel (grün).
Katenoid
Die durch Rotation der Kettenlinie um die x-Achse erzeugte Rotationsfläche wird als Katenoid bezeichnet und ist eine Minimalfläche.
Traktrix
Die Kettenlinie ist die Evolute zu der Traktrix (Schleppkurve).
Beispiele
Für
= 100 m und einen Mastabstand
von 200 m (also Spezialfall
)
wird ein 2·117,5 m langes Seil benötigt:
.
Der Durchhang beträgt 54 m. Für ein Stahlseil mit 100 cm² Querschnitt
wiegt eine Seilhälfte 9,2 t. Die entsprechende Gewichtskraft von
9·104 N
ist die vertikale Kraft an einer Aufhängung. Die horizontale Kraft an einer
Aufhängung beträgt 7,7·104 N.
Beträgt
etwa 20,2 % der gesamten Breite
,
so ist der Durchhang
gleich der Breite
(quadratförmige Gesamtabmessungen). Dieser Fall liegt beispielsweise vor beim Gateway Arch (siehe unten im Abschnitt Architektur), der 630 Fuß breit und
ebenso hoch ist. Die exakte Formel
mit a = 127,7 Fuß und w/2 = 315 Fuß ist im Inneren des Denkmals ausgestellt.
Anwendungen in der Architektur
Einer der Kettenlinie analoge Stützlinie folgt der scherkräftefreie Bogen:
- Die Nubische Tonne, ein Tonnengewölbe, ist eine Variante des Nubischen Gewölbes, einer Gewölbebauweise im Lehmbau ohne Schalung und häufig ohne Lehren, die ihren Namen von traditionellen Bauformen in Nubien hat. Um die größtmögliche Stabilität zu erreichen, folgt die Stützlinie in der Regel der Kettenlinie.
- Ein frühes europäisches Beispiel ist die nach Plänen von Christopher Wren nach 1666 erbaute St Paul’s Cathedral in London. Zwischen eine äußere und innere hölzerne Halbkugel ließ er ein Katenoid legen, das die Schwere der Laterne aufnahm, aber selbst ein geringeres Baugewicht ermöglichte. Die Kurve wurde damals noch empirisch angenähert.
- Querschnitt des Daches des Bahnhofs Budapest Ost (Keleti) (Ungarn) bildet eine Kettenlinie. Erbaut von 1881/84. Konstrukteur: János Feketeházy.
- Antoni Gaudí nutzte häufiger das darauf fußende Konstruktionsprinzip, unter anderem bei der Sagrada Família in Barcelona. Das Modell der ähnlichen Kirche der Colònia Güell wurde ebenfalls empirisch ermittelt, nämlich „kopfüber“ durch hängende Schnüre mit entsprechenden Gewichten (um 1900; Original in einem Brand verloren)
- Die Stützline des 192 m hohen Gateway Arch in St. Louis (2018) ist durch die unterschiedliche Stärke des Bogens keine echte Kettenlinie.
Fotos
-
 Experiment: stehende Kettenlinie
Experiment: stehende Kettenlinie -
 Bau eines Brennofens
Bau eines Brennofens -
 Sheffield Winter Garden
Sheffield Winter Garden -
 Gateway Arch in St. Louis
Gateway Arch in St. Louis -
 Casa Milà von Antoni Gaudí
Casa Milà von Antoni Gaudí -
 Architekturmodell von Gaudí
Architekturmodell von Gaudí -
 Querschnitt des Daches des Ostbahnhofs in Budapest (Ungarn)
Querschnitt des Daches des Ostbahnhofs in Budapest (Ungarn) -
 Capilano Suspension Bridge, eine Seilbrücke
Capilano Suspension Bridge, eine Seilbrücke -
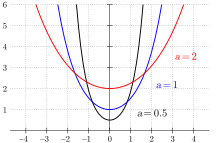
 Variation des Parameters a, oder verschieden voneinander entfernte Aufhängungspunkte
Variation des Parameters a, oder verschieden voneinander entfernte Aufhängungspunkte -
 Zeichnung von Christiaan Huygens
Zeichnung von Christiaan Huygens -
 Die Seile von Freileitungen folgen der Kettenlinie
Die Seile von Freileitungen folgen der Kettenlinie -
 Spinnenfäden folgen ungefähr der Kettenlinie, hier durch Tautropfen betont
Spinnenfäden folgen ungefähr der Kettenlinie, hier durch Tautropfen betont
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.12. 2021