Minimalfläche

Eine Minimalfläche ist eine Fläche im Raum, die lokal minimalen Flächeninhalt hat. Derartige Formen nehmen beispielsweise Seifenhäute an, wenn sie über einen entsprechenden Rahmen (wie etwa einen Blasring) gespannt sind.

In mathematischer Sprache sind Minimalflächen die kritischen Punkte des Flächeninhaltsfunktionals

$A({\mathbf x})=\int {\sqrt {g(u)}}\,{\mathrm d}^{{n}}u$ .

Hierbei sind die Größen $g(u):=\operatorname {det} (g_{ij}(u))_{i,j=1,\dotsc ,n}$ und $g_{{ij}}(u)=\left({\tfrac {\partial {\mathbf x}}{\partial u_{i}}}\right)^{T}{\tfrac {\partial {\mathbf x}}{\partial u_{j}}}$ für $i,j=1,\dotsc ,n$ erklärt (vgl. Hesse-Matrix). Man beachte, dass eine Minimalfläche nicht notwendig minimalen Flächeninhalt hat, sondern lediglich ein stationärer Punkt des Flächeninhaltsfunktionals ist. Man kann zeigen, dass das Verschwinden der ersten Variation des Flächeninhaltsfunktionals in zwei Raumdimensionen äquivalent zum Verschwinden der mittleren Krümmung H ist, falls die betrachtete Mannigfaltigkeit hinreichend regulär ist.

Minimalflächen stehen schon seit dem 19. Jahrhundert im Blickpunkt mathematischer Forschung. Ein wesentlicher Beitrag dazu waren die Experimente des belgischen Physikers Joseph Plateau.

Enneperfläche als Beispiel einer Minimalfläche

Ausführungen zur Existenztheorie in zwei Veränderlichen

Ein zweidimensionaler Parameterbereich stellt immer eine Besonderheit dar. Denn mit den Werkzeugen der Funktionentheorie kann man viel weitergehende Aussagen als in höheren Raumdimensionen erzielen. Dadurch kann man sich zum Beispiel immer auf die Kreisscheibe als Parameterbereich mit dem Riemannschen Abbildungssatz zurückziehen. Auch gilt der Uniformisierungssatz nur in zwei Raumdimension. Er erlaubt es, isotherme Parameter einzuführen, die bei der Lösung im parametrischen Falle benötigt werden. Darum ist die Theorie in zwei Veränderlichen auch besonders weit entwickelt.

Formulierung als Variationsproblem

Eine Fläche ist genau dann eine Minimalfläche, wenn sie an jedem Punkt die mittlere Krümmung null hat. Damit stellt sich eine Minimalfläche als Spezialfall einer Fläche vorgeschriebener mittlerer Krümmung dar. Diese entziehen sich ebenfalls nicht der Variationsrechnung, sie sind Minima des Hildebrandtschen Funktionals

$A({\mathbf x})=\iint {\big (}|{\mathbf x}_{u}\times {\mathbf x}_{v}|+2(Q({\mathbf x}),{\mathbf x}_{u},{\mathbf x}_{v}){\big )}\,{\mathrm d}u\,{\mathrm d}v$ .

Die Eulerschen Gleichungen als notwendige Minimalitätsbedingungen dieses Funktionals sind das nach Franz Rellich benannte H-Flächen-System

$\Delta {\mathbf x}=2H{\mathbf x}_{u}\times {\mathbf x}_{v},\qquad {\mathbf x}_{u}^{2}-{\mathbf x}_{v}^{2}=0={\mathbf x}_{u}{\mathbf x}_{v}$ .

Hierbei ist $H=\operatorname {div}\,Q$ die mittlere Krümmung.

Parametrischer Fall

Für dieses Funktional stellt sich die Frage nach der Existenz von lokalen Minima bei vorgegebener stetiger Randkurve endlicher Länge. Diese Aufgabe bezeichnet man in der Literatur auch als Plateausches Problem. Unter Annahme einer Kleinheitsbedingung an die mittlere Krümmung, die im Minimalflächenfall immer erfüllt ist, kann diese Frage positiv beantwortet werden. Um sich davon zu überzeugen, minimiert man gleichzeitig und das Energiefunktional

$E({\mathbf x})=\iint {\Big (}{\frac 12}|\nabla {\mathbf x}|^{2}+2(Q({\mathbf x}),{\mathbf x}_{u},{\mathbf x}_{v}){\Big )}\,{\mathrm d}u\,{\mathrm d}v$

unter Einführung sogenannter fast-isothermer Parameter.

Im Jahre 1884 bewies Herrmann Amandus Schwarz den Satz

In der Menge der stetig differenzierbaren, einfach geschlossenen, orientierbaren Flächen vom Geschlecht Null (d.h. ohne Löcher) ist die Kugel die Fläche, die bei gegebener Oberfläche den größten Rauminhalt umgrenzt.

Verzweigungspunkte

Stellen, an denen die Lösung $|{\mathbf x}_{u}\times {\mathbf x}_{v}|=0$ erfüllt, nennt man Verzweigungspunkte. Verzweigungspunkte sind interessant, weil an diesen Punkten die Parametrisierung singulär werden kann. Schlimmer noch ist die Möglichkeit, dass die Lösung lokal keine Fläche mehr ist, sondern nur noch eine Kurve.

Nun liefern funktionentheoretische Überlegungen, die wesentlich durch Arbeiten von Carleman und Vekua inspiriert sind, dass die Lösung höchstens endlich viele solcher Verzweigungspunkte haben kann. Leider schließt die obige Methode solche Verzweigungspunkte nicht a priori aus. Erst mit dem aufwändigen Satz von Gulliver-Alt-Osserman gelingt dies a posteriori. Darum besteht der Wunsch, das Plateausche Problem in der Klasse der verzweigungspunktfreien H-Flächen zu lösen. Das ist bis heute eine offene Frage.

Nichtparametrischer Fall, Minimalflächengleichung

Die obige Methode führt allerdings nur für konstantes zum Erfolg. Hängt die mittlere Krümmung zusätzlich von der Lösung ab, kann man im Falle eines Graphen immer noch etwas tun: Ist $\mathbf x$ ein Graph, so schreibt er sich als ${\mathbf x}(u,v)=(u,v,\zeta (u,v))^{T}$ und die Funktion $\zeta$ erfüllt die nichtparametrische Gleichung vorgeschriebener mittlerer Krümmung

$(1+\zeta _{v}^{2})\zeta _{{uu}}-2\zeta _{u}\zeta _{v}\zeta _{{uv}}+(1+\zeta _{u}^{2})\zeta _{{vv}}=H(u,v,\zeta (u,v))$ .

Im Fall von Minimalflächen ist H=0 und die Gleichung wird als Minimalflächengleichung bezeichnet.

Ein tiefliegendes Existenzresultat liefert die Lösbarkeit des Dirichletproblems dieser partiellen Differentialgleichung ebenfalls unter Annahme einer Kleinheitsbedingung und weiteren technischen Voraussetzungen. Die Eindeutigkeit ist durch ein Maximumprinzip für die Differenz zweier Lösungen ebenfalls geklärt. Darüber hinaus sind Graphen wegen

$|\mathbf {x} _{u}\times \mathbf {x} _{v}|={\sqrt {1+\nabla \zeta (u,v)^{2}}}\geq 1$

immer verzweigungspunktfrei.

Beispiele von Minimalflächen

Hier werden mehrere Beispiele verschiedenster Minimalflächen im dreidimensionalen euklidischen Raum angegeben. Manche davon kann man nicht ohne Selbstschnitte in den dreidimensionalen Raum einbetten. Andere sind nicht auf den Rand ihres Definitionsbereiches stetig fortsetzbar, wie das erste Beispiel zeigt.

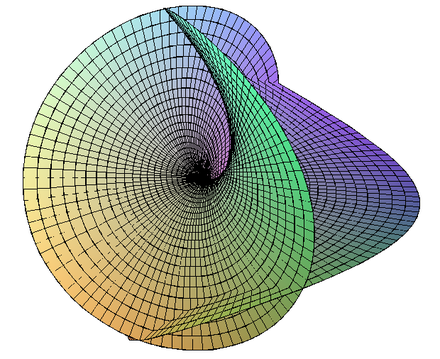
Die Minimalfläche von H. F. Scherk

Zusammenhangskomponente der Minimalfläche von Scherk zum Parameter c=1

Die Minimalfläche von Heinrich Ferdinand Scherk (1835): Wir suchen alle Lösungen der nichtparametrischen Minimalflächengleichung, die sich in der Form $z=\zeta {\big (}u,v{\big )}=f(u)+g(v)$ schreiben lassen und den Bedingungen $\zeta {\big (}0,0{\big )}=0$ , $\nabla \zeta (0,0)=0$ genügen. Wir setzen diese Struktur zunächst in die Minimalflächengleichung ein und erhalten:

$0\,\,=(1+\zeta _{v}^{2})\zeta _{{uu}}-2\zeta _{u}\zeta _{v}\zeta _{{uv}}+(1+\zeta _{u}^{2})\zeta _{{vv}}$

$={\big (}1+(g'(v))^{2}{\big )}f''(u)+(1+(f'(u))^{2})g''(v)$

Äquivalentes Umstellen liefert

$-{\frac {f''(u)}{1+(f'(u))^{2}}}=c={\frac {g''(v)}{1+(g'(v))^{2}}}$

mit einem $c\in {\mathbb R}$ . Nach der Theorie der gewöhnlichen Differentialgleichungen existiert jeweils genau eine Lösung für die Anfangswertprobleme

$f''{\big (}u{\big )}+c(1+(f'(u))^{2})=0$ zu den Daten $f(0)=0,\,\,f'(0)=0$

und

$g''{\big (}v{\big )}-c(1+(g'(v))^{2})=0$ zu den Daten $g(0)=0,\,\, g'(0)=0.$

Diese Lösungen lauten

$f(u)={\frac 1c}\log \cos(cu)$

und

$g(v) = -\frac 1 c \log\cos ( cv).$

mehrere Zusammenhangskomponenten der Scherkschen Minimalfläche zum Parameter c = 0,2

Hier bleibt zu bemerken, dass wir noch an den Anfangswerten $f{\big (}0)=d$ und $g{\big (}0)=-d$ mit einem $d\in {\mathbb R}$ variieren könnten. Jedoch kann man oBdA wegen der Strukturbedingung und der Tatsache, dass die Funktionen selbst nicht in den gewöhnlichen Differentialgleichungen auftreten, d=0 fordern. Somit erhalten wir:

$z=\zeta {\big (}u,v{\big )}=f(u)+g(v)={\frac 1c}\log {\frac {\cos(cu)}{\cos(cv)}}$

Wir bemerken, dass diese Minimalfläche auf den Quadraten

$\Omega :={\big \{}(u,v)\in \mathbb {R} ^{2}:\,{\big |}u+k{\frac {\pi }{c}}{\big |}<{\frac {\pi }{2c}},{\big |}v+l{\frac {\pi }{c}}{\big |}<{\frac {\pi }{2c}}\quad {\text{für}}\quad k,l\in \mathbb {Z} \quad {\text{mit}}\quad k\equiv l{\pmod {2}}{\big \}}$

erklärt und nicht darüber hinaus fortsetzbar ist. Diese Fläche ist als Graph in den dreidimensionalen Raum einbettbar.

Das Katenoid

Katenoid zum Parameter c=1

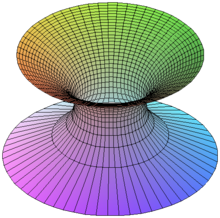
Wenn man die Kettenlinie um die x-Achse rotieren lässt, erhält man ebenfalls eine in den dreidimensionalen Raum eingebettete Minimalfläche – ein Katenoid. Katenoide sind die einzigen Minimalflächen, die gleichzeitig auch Rotationsflächen sind. Sie genügen zu einem positiven Parameter c > 0 der Gleichung

$\sqrt{x^2+y^2} = c\,\operatorname{cosh}\frac z c.$

Es war eine der ersten von Plateau experimentell gefundenen Lösungen des Plateauschen Problems. Hierbei waren die Randdaten zwei Kreisringe, welche die obere und untere Randkurve eines Kegelstumpfes oder Zylinders bilden.

Das Katenoid als Minimalfläche stammt von Leonhard Euler um 1740.

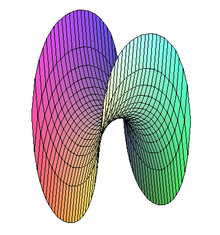
Die Wendelfläche

Helikoid zum Parameter c=1

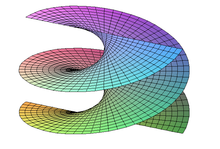
Eng verwandt mit dem Katenoid ist die Wendelfläche oder das Helikoid. Diese Fläche geht aus einem Katenoid durch eine unstetige, aber isometrische Deformation hervor. Zu einem Parameter c > 0 genügt sie den folgenden Gleichungen:

$x{\big (}u,v)=u\cos v$

$y{\big (}u,v)=u\sin v$

$z{\big (}u,v)=cv$

Auch diese Minimalfläche ist in den dreidimensionalen Raum eingebettet.

Die Wendelfläche als Minimalfläche stammt von Jean-Baptiste Meusnier de la Place (1776). Die Helikoide hat das topologische Geschlecht 0. David Allen Hoffman und Kollegen konstruierten in den 1990er Jahren mit Computerhilfe vollständige in den dreidimensionalen euklidischen Raum einbettbare Minimalflächen mit unendlichem und beliebigem endlichen topologischen Geschlecht, wobei der strenge Beweis nur für unendliches Geschlecht und für Geschlecht 1 (Michael Wolf, Hoffman, Matthias Weber 2009) erfolgte. Für Genus 0 sind die Helikoide (worunter als Spezialfall auch die Katenoide fällt) und die Ebene die einzigen vollständigen einbettbaren Minimalflächen (William Meeks, Harold William Rosenberg 2005).

Die Henneberg-Fläche

Hennebergsche Minimalfläche

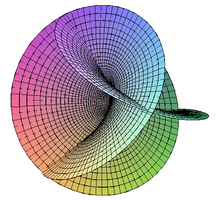
Die Henneberg-Fläche ist ein Beispiel einer Minimalfläche, die das Bild einer Immersion in den dreidimensionalen euklidischen Raum ist, aber nicht in den dreidimensionalen euklidischen Raum eingebettet werden kann. Ihre Bestimmungsgleichungen lauten:

$x(u,v)=2\sinh u\cos v-{\frac 23}\sinh(3u)\cos(3v)$

$y(u,v)=2\sinh u\sin v+{\frac {2}{3}}\sinh(3u)\sin(3v)$

$z(u,v)=2\cosh(2u)\cos(2v)$

Außerdem ist diese Fläche nicht orientierbar: Anschaulich gesprochen kann man nicht entscheiden, welche Seite dieser Fläche oben und welche unten ist.

Sie ist nach Lebrecht Henneberg benannt, der sie in seiner Dissertation 1875 einführte.

Höhere Raumdimensionen

In hohen Raumdimensionen ist ein Zugang zum Plateauschen Problem schwer denkbar. Hier hat man lediglich die Möglichkeit, die Lösung als Graph aufzufassen. Die Minimalflächengleichung für den Graphen schreibt sich

$\operatorname {div}{\frac {\nabla \zeta }{{\sqrt {1+\nabla \zeta ^{2}}}}}=0$ .

Durch die Theorie der schwachen Lösbarkeit elliptischer Randwertprobleme kann man auch in dieser Situation die Existenz von Lösungen garantieren. Nachfolgende Regularitätsbetrachtungen liefern eine klassische Lösung. Wie in zwei Raumdimensionen erhält man auch hier die Eindeutigkeit durch ein Maximumprinzip für die Differenz zweier Lösungen.

Einige interessante Aussagen über Minimalflächen

Auf Grund der relativ einfachen Struktur der Gleichungen, denen Minimalflächen genügen, kann man einige bekannte Aussagen, die man besonders für holomorphe oder harmonische Funktionen kennt, auch auf Minimalflächen in zwei Veränderlichen übertragen.

Maximumprinzip

Für eine Minimalfläche $\mathbf x$ gilt die Ungleichung

$\sup _{{w\in B}}|{\mathbf x}(w)|\leq \sup _{{w\in \partial B}}|{\mathbf x}(w)|$ .

Die Minimalfläche nimmt ihr Maximum also auf dem Rand des Gebietes, auf dem sie erklärt ist, an.

Uniformisierende Abbildungen

In der Geodäsie kann man sogenannte isotherme Parameter einführen. Die Abbildung, die das bewerkstelligt, heißt uniformisierende Abbildung. Uniformisierende Abbildungen von Minimalflächen sind harmonische Funktionen.

Reellanalytischer Charakter

Minimalflächen sind, solange sie in isothermen Parametern vorliegen, reellanalytische Funktionen im Inneren des Gebietes, in dem sie erklärt sind. Das bedeutet, die Parameterdarstellung kann in jedem Punkt des Gebietes in einer Umgebung dieses Punktes in eine konvergente Potenzreihe entwickelt werden. Daher ist sie beliebig oft differenzierbar. Ist darüber hinaus die Randkurve in einem Punkt reellanalytisch, so kann die Minimalfläche in einer Umgebung dieses Punktes reellanalytisch über den Rand hinaus fortgesetzt werden.

Die Sätze von Bernstein und Liouville

Der Satz von Sergei Bernstein für Minimalflächen lautet:

Eine auf ganz $\mathbb R^2$ erklärte Lösung $\zeta {\big (}u,v{\big )}$ der nichtparametrischen Minimalflächengleichung erfüllt notwendig die Gleichung

$\zeta {\big (}u,v{\big )}=au+bv+c$

mit Konstanten $a,b,c\in \mathbb {R}$ .

Die Frage nach der Verallgemeinerung auf höhere Dimensionen ist als Problem von Bernstein bekannt und wurde durch Ennio de Giorgi, Enrico Bombieri und andere gelöst.

Aus diesem Satz folgt sofort der Satz von Liouville für Minimalflächen:

Eine auf ganz $\mathbb R^2$ erklärte beschränkte Lösung $\zeta {\big (}u,v{\big )}$ der nichtparametrischen Minimalflächengleichung erfüllt notwendig

$\zeta {\big (}u,v{\big )}=\operatorname {const}$ .

Dies ist ein Analogon des Satzes von Liouville der Funktionentheorie.

Der Flächeninhalt einer Minimalfläche

Der Flächeninhalt einer Minimalfläche $\mathbf x$ mit der Einheitsnormalen $\mathbf n$ schreibt sich in der Form

$A=\oint (\mathbf {n} ,\mathbf {x} ,\mathrm {d} \mathbf {x} )$ .

Dabei muss angenommen werden, dass die Randkurve einfach geschlossen und stetig differenzierbar ist.

Darstellungsformeln

Um Minimalflächen besser zu verstehen, genügt es nicht, nur die Differentialgleichungen zu betrachten, denen sie genügen, sondern man sollte auch spezielle Darstellungen der Lösung ermitteln.

Komplexe Darstellung

Unter Einführung isothermer Parameter u und v erhalten wir zunächst das H-Flächen-System für H=0:

$\Delta {\mathbf x}=0,\qquad {\mathbf x}_{u}^{2}-{\mathbf x}_{v}^{2}=0={\mathbf x}_{u}{\mathbf x}_{v}$

Damit schreibt sich die Gleichung zweiter Ordnung in der Form

${\frac {\partial ^{2}{\mathbf x}}{\partial z^{1}\partial z^{2}}}=0$

mit den komplexen Veränderlichen $z^{1}=u+iv$ und $z^{2}=u-iv$ und wir erhalten die Darstellung

$2{\mathbf x}={\mathbf y}(z^{1})+{\mathbf z}(z^{2})\qquad$ und $\qquad ({\mathbf y}')^{2}=0=({\mathbf z}')^{2},\qquad {\mathbf y}'{\mathbf z}'\neq 0$ .

Wir nennen eine komplexe Kurve ${\mathbf y}(z)$ , die den Bedingungen $({\mathbf y}')^{2}=0$ und ${\mathbf y}'\neq 0$ genügt, eine isotrope Kurve. Weiter nennen wir eine Fläche ${\mathbf x}(u,v)$ , die sich in der Form ${\mathbf x}(u,v)={\mathbf y}(u)+{\mathbf z}(v)$ schreiben lässt, eine Schiebfläche.

Eine verallgemeinerte Definition von Minimalflächen ist:

Eine Minimalfläche ist eine Schiebfläche, deren Erzeugende isotrope Kurven sind.

Reelle Minimalflächen erfüllen dann die Bedingungen

$\overline {z^{1}}=z^{2}\qquad$ und $\qquad {\mathbf z}(\overline {z^{1}})=\overline {{\mathbf y}(z_{1})}$ .

Integraldarstellung

Die nach Karl Weierstraß und Alfred Enneper benannte Darstellungsformel liefert einen Zusammenhang zwischen der Differentialgeometrie und der Funktionentheorie. Nun hat Weierstraß großen Einfluss auf das Entstehen der Funktionentheorie gehabt. Diese Darstellungsformel war einer der Gründe, warum dieser relativ neue Zweig der Mathematik ernst genommen wurde und so erfolgreich war und ist. Er hat herausgefunden, dass sich jede nichtkonstante Minimalfläche ${\mathbf x}(w)={\big (}x(w),y(w),z(w){\big )}$ als Integral mit den beiden holomorphen Funktionen g und h schreiben lässt. Genauer gilt für die Komponenten:

$x(w)=c_{1}+\operatorname {Re}\int _{{w_{0}}}^{w}{\frac {h(\zeta )\left(1-g(\zeta )^{2}\right)}{2}}{\mathrm d}\zeta$ ,

$y(w)=c_{2}+\operatorname {Re} \int _{w_{0}}^{w}{\frac {h(\zeta )\left(1+g(\zeta )^{2}\right)}{2}}\mathrm {d} \zeta$ ,

$z(w)=c_{3}+\operatorname {Re}\int _{{w_{0}}}^{w}h(\zeta )g(\zeta ){\mathrm d}\zeta$

Diese Darstellungsformel ermöglicht es, mit Hilfe moderner Computeralgebrasysteme Bilder von beliebigen Minimalflächen zu erzeugen. Beispielsweise wurden einige Bilder von Minimalflächen in diesem Artikel unter Verwendung dieser Formeln mit dem Programm Maple erstellt.

Integralfreie Darstellung

Da wir gesehen haben, dass es, um die Differentialgleichung H = 0 zu integrieren, genügt, isotrope Kurven zu bestimmen, erhalten wir für reelle Minimalflächen $\mathbf {x} (w)={\big (}x(w),y(w),z(w){\big )}$ die sogenannte integralfreie Darstellung

$x(w)=\operatorname {Re}\left(\pm i\left(f(w)-wf'(w)-{\frac {1-w^{2}}{2}}f''(w)\right)\right)$

$y(w)=\operatorname {Re}\left(f(w)-wf'(w)+{\frac {1+w^{2}}{2}}f''(w)\right)$

$z(w)=\operatorname {Re}\left(-i{\big (}f'(w)-wf''(w){\big )}\right)$

mit einer holomorphen Funktion f=f(w) , die der Voraussetzung $f'''\neq 0$ genügen muss. Ebenen entziehen sich somit dieser Darstellung. Um nun die Bedeutung der komplexen Veränderlichen für eine reelle Minimalfläche zu klären, liefert eine langwierige Rechnung

$w={\frac {n_{1}+in_{2}}{-1+n_{3}}}$ bzw. ${\frac 1w}={\frac {n_{1}+in_{2}}{-1+n_{3}}}$ ,

hierbei ist $\mathbf {n} =(n_{1},n_{2},n_{3})$ der Einheitsnormalenvektor der Minimalfläche. Wir fassen zusammen: Durch Angabe der komplexen Zahl bzw. $1/w$ ist der Einheitsnormalenvektor $\mathbf n$ der Minimalfläche festgelegt. Umgekehrt hängt bzw. $1/w$ lediglich von $\mathbf n$ ab. Die Aussagen dieses Abschnitts sind insbesondere dem Buch Elementare Differentialgeometrie von W. Blaschke und K. Leichtweiß zu entnehmen, siehe dazu auch Literatur.

Bemerkungen zum Flächeninhaltsfunktional

Wir werden dieses Funktional zunächst allgemein herleiten und die Invarianz unter positiv orientierten Parametertransformationen zeigen. Schließlich werden wir die ein- und zwei-dimensionalen Spezialfälle explizit ausrechnen.

Herleitung und Parameterinvarianz

Wir beachten, dass sich unsere Minimalfläche als m-dimensionale Mannigfaltigkeit im n-dimensionalen reellen Vektorraum auffassen lässt. Das ist aufgrund des Einbettungssatzes von Nash immer möglich. Wir erklären zunächst den metrischen Tensor

$g_{{ij}}(u):={\frac {\partial {\mathbf x}(u)}{\partial u_{i}}}{\frac {\partial {\mathbf x}(u)}{\partial u_{j}}}$

mit der Determinante

$g(u):=\operatorname {det} (g_{ij}(u))_{i,j=1,\dotsc ,m}$ .

Wir erinnern uns, dass sich ein Inhalt einer m-dimensionalen Fläche als m-dimensionales Integral über die charakteristische Funktion dieser Fläche ergibt. Eine charakteristische Funktion ist überall identisch eins auf der Menge und sonst identisch null. Damit müssen wir lediglich das Oberflächenelement geeignet ausdrücken. Wir erklären in einem festen Punkt u die Tangentialvektoren

${\frac {\partial {\mathbf x}(u)}{\partial u_{i}}}$ für $i,j=1,\dotsc ,m$

und wählen Vektoren $\xi _{m+1},\dotsc ,\xi _{n}$ , sodass das System

$(\mathbf {x} _{u_{1}},\dotsc ,\mathbf {x} _{u_{m}},\xi _{m+1},\dotsc ,\xi _{n})$

positiv orientiert ist und die beiden Bedingungen $(\mathbf {x} _{u_{i}},\xi _{j})=0$ und ${\big (}\xi _{i},\xi _{j})=\delta _{ij}$ für alle sinnvollen Werte von i und j erfüllt. Somit schreibt sich das Oberflächenelement:

${\begin{aligned}\mathrm {d} \sigma (u)&=\operatorname {det} (\mathbf {x} _{u_{1}},\dotsc ,\mathbf {x} _{u_{m}},\xi _{m+1},\dotsc ,\xi _{n})\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\\&={\sqrt {\operatorname {det} ((\mathbf {x} _{u_{1}},\dotsc ,\xi _{n})^{T}(\mathbf {x} _{u_{1}},\dotsc ,\xi _{n}))}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\\&={\sqrt {\operatorname {det} (g_{ij}(u))_{i,j=1,\dotsc ,m}}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\\&={\sqrt {g(u)}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\end{aligned}}$

Für die Determinante zweier $m\times n$ -Matrizen mit $m\leq n$ gilt:

$\operatorname {det} (A^{T}B)=\sum _{1\leq i_{1}<\dotsb <i_{m}\leq n}\operatorname {det} A_{i_{1}\dotso i_{m}}\operatorname {det} B_{i_{1}\dotso i_{m}}$

Dabei bezeichnet $A_{i_{1}\dotso i_{m}}$ diejenige Teilmatrix von , die nur aus den Zeilen $i_{1},\dotsc ,i_{m}$ besteht. Damit können wir das Oberflächenelement in der Form

$\mathrm {d} \sigma (u)={\sqrt {\sum _{1\leq i_{1}<\dotsb <i_{m}\leq n}\left({\frac {\partial {\big (}\mathbf {x} _{u_{i_{1}}},\dotsc ,\mathbf {x} _{u_{i_{m}}}{\big )}}{\partial {\big (}u_{1},\dotsc ,u_{m}{\big )}}}\right)^{2}}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}$

schreiben. Mit Hilfe der Transformationsformel stellen wir nun die Invarianz unter gleichsinnigen Parametertransformationen des Oberflächenelements und damit des Flächeninhaltsfunktionals fest.

Der ein- und zweidimensionale Inhalt

In einer Raumdimension reduziert sich dieses Funktional auf die gewöhnliche Weglänge:

$A({\mathbf x})=\int |{\mathbf x}'(u)|\,{\mathrm d}u$

Hat man eine zweidimensionale Fläche vorliegen, die in den dreidimensionalen Raum eingebettet ist, erhält man mit der Identität von Lagrange:

$EG-F^{2}=|{\mathbf x}_{u}\times {\mathbf x}_{v}|^{2}$

Damit gilt für das Flächeninhaltsfunktional:

$A({\mathbf x})=\iint |{\mathbf x}_{u}\times {\mathbf x}_{v}|\,{\mathrm d}u{\mathrm d}v$

Literatur

Wilhelm Blaschke, Kurt Leichtweiß: Elementare Differentialgeometrie (= Grundlehren der mathematischen Wissenschaften. Band 1). Springer-Verlag, 1973,
Johannes C. C. Nitsche: Vorlesungen über Minimalflächen (= Grundlehren der mathematischen Wissenschaften. Band 199). Springer-Verlag, 1975.
Friedrich Sauvigny: Partielle Differentialgleichungen der Geometrie und der Physik. Springer-Verlag, 2004 f., 2 Bände.

Basierend auf einem Artikel in:

Wikipedia.de