Scherung (Mechanik)

Der Umfang eines durch Torsion um den Winkel φ verwundenen Rundstabes erfährt die Schubverzerrung γ und Schubspannung τ.
Ein auf den Umfang aufgemaltes Quadrat würde durch die Torsion zu einem Parallelogramm verzerrt.

Eine Scherung resultiert in der Mechanik aus der Wirkung eines versetzt angeordneten Kräftepaars, der Scherkraft oder Schubkraft, auf einen Körper und führt zur Schubverzerrung des zwischen den Kräften liegenden Bereichs. Das heißt, ein zuvor rechteckiger Bereich würde sich in ein Parallelogramm verformen, siehe auch: Scherung (Geometrie).
Das Kräftepaar kann auch durch ein auf den Körper wirkendes Moment hervorgerufen werden. Ein Kräftepaar, welches auf einer Linie liegt, bewirkt statt der Schubverzerrung eine Dehnung des Körpers.

Zugleich mit der Schubverzerrung bewirkt das Kräftepaar eine Scherspannung im Material, die auch als Schubspannung bezeichnet wird. Der Schubmodul beschreibt die Größe der Verzerrung relativ zur anliegenden Schubspannung.

In der Kontinuumsmechanik wird Scherung und Schubverzerrung synonym benutzt, siehe Abschnitt Kinematik der Scherung.
In der technischen Mechanik wird unter Scherung auch Scherbelastung verstanden, siehe Abschnitt Dynamik der Scherung.

Von reiner Scherung wird gesprochen, wenn in der betrachteten Schnittebene keine Normaldehnungen oder keine Normalspannungen vorkommen.

Scherung tritt unter anderem bei der Torsion wie im Bild oder der Querkraftbeanspruchung von Trägern auf, ist aber auch in viskosen Fluiden (Flüssigkeiten oder Gase) bedeutsam.

Einführung

Die Scherung von Flüssigkeiten und Gasen wird in einem eigenen Abschnitt unten behandelt.

Makroskopische Betrachtung

Scherung eines Körpers (grau) durch zwei parallel zueinander in entgegengesetzter Richtung wirkende Kräfte (rot)

Zwei an einem Körper angreifende, parallel zueinander in entgegengesetzter Richtung wirkende Kräfte bewirken eine Scherung des Körpers und heißen daher Scherkräfte, siehe Bild. Bei einer Torsion werden parallel zueinander liegende Oberflächen gegeneinander verdreht, was auch eine Scherung darstellt, siehe einleitendes Bild oben. Die Länge des Gegenstands sowie sein Querschnitt bleiben dabei idealerweise unverändert. Die scherenden Kräfte wirken stets tangential zur Körperoberfläche. Typische Beispiele für Scherkräfte kommen in Niet- und Bolzenverbindung vor, siehe Abscherung (Statik). Die Schneidekanten von Scheren trennen das zu zerschneidende Material durch Scherung (Scherschneiden).

Mikroskopische Betrachtung

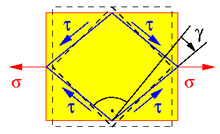
Hauptscherung τ bei einachsigem Zug σ

Die Festigkeitslehre und Kontinuumsmechanik interessieren sich für die lokalen Verhältnisse in einem Körper unter Scherung, denn dort entscheidet sich, ob sich der Körper beispielsweise elastisch oder plastisch verformt. Die lokalen Verhältnisse werden zugänglich, wenn der Körper gedanklich zerschnitten wird und so an der Schnittebene Schnittspannungen (Vektoren mit der Dimension Kraft pro Flächeninhalt) entstehen, die von der Orientierung der Schnittebene abhängen. Die Schnittebene kann in einem Punkt so gelegt werden, dass in ihr die Schubspannung, die definitionsgemäß parallel zur Schnittebene wirkt, maximal ist. Normalspannungen wirken im Gegensatz dazu senkrecht zur Schnittebene.

Die in der makroskopischen Betrachtung herangezogenen Belastungen führen zu Schubspannungen, die im Vergleich zu den Hauptnormalspannungen (kurz Hauptspannungen) maximal, nämlich betraglich gleich sind. Hier sind zwei Hauptspannungen entgegengesetzt gleich groß (siehe auch das Beispiel unten) und der Mittelpunkt des Mohr’schen Spannungskreises liegt im Spannungsraum im Ursprung, so dass die maximale Schubspannung betraglich genauso groß ist wie die Hauptspannungen. Am Mohr’schen Spannungskreis lässt sich auch ablesen, dass die maximalen Schubspannungen im 45°-Winkel zu den Hauptspannungsrichtungen auftreten, die wiederum senkrecht zu Schnittebenen sind, in denen keine Schubspannungen vorkommen, siehe Bild.

Sind zwei Hauptspannungen gleich, dann degeneriert der Mohr’sche Spannungskreis zu einem Punkt. Sind alle drei Hauptspannungen gleich, dann befindet sich der materielle Punkt unter allseitigem Druck/Zug und es treten in keiner Ebene Schubspannungen auf. In allen anderen Fällen gibt es Schnittebenen, in denen eine maximale und nicht verschwindende Scherbelastung stattfindet.

Die in der makroskopischen Betrachtung vorgestellten Fälle stellen aus Sicht der Schubspannungshypothese ungünstigste Belastungen dar, denn nach dieser Hypothese sind die Schubspannungen für das Versagen eines Werkstoffs verantwortlich. Demzufolge lohnt es sich, den Schubanteilen besondere Aufmerksamkeit zu schenken und das Bezugssystem entsprechend auszurichten.

Kinematik der Scherung

Streckung und Scherung der Tangenten (rot und blau) an materiellen Linien (schwarz) im Zuge einer Deformation

Zur Veranschaulichung einer Scherung kann man sich ein Buch vorstellen: verschiebt man die Buchdeckel parallel gegeneinander, bilden Buchrücken und Seitenstapel einen Winkel ungleich 90°. Die Abweichung vom rechten Winkel ist die Schubverzerrung oder Gleitung γ.

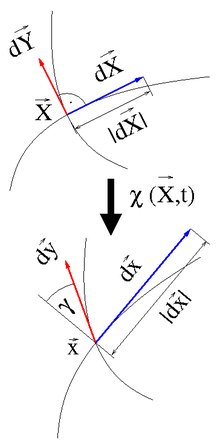
Mathematisch wird eine lokale Verformung wie im Bild rechts betrachtet. Zwei sich im Referenzzustand (oberer Bildteil) kreuzende materielle Linien (die man sich als oberflächig eingeritzte Linien vorstellen kann) schließen einen rechten Winkel ein, der zwischen ihren Tangentenvektoren $\mathrm{d}\vec X$ und $\mathrm{d}\vec Y$ gemessen wird. Wie üblich werden die x- und y-Koordinaten nach dem Schema x→1 und y→2 durchnummeriert. Im Zuge einer Deformation – beschrieben mit der Bewegungsfunktion $\vec\chi$ – ändert sich der Winkel γ zwischen den Tangentenvektoren gemäß

$\sin (\gamma ): =\frac{\mathrm{d}\vec{x}\cdot \mathrm{d}\vec{y}}{|\mathrm{d}\vec{x}||\mathrm{d}\vec{y}|} =\frac{2\hat{G}_{1}\cdot\mathbf{E}\cdot\hat{G}_{2}} {\sqrt{1+2\hat{G}_{1}\cdot \mathbf{E}\cdot\hat{G}_{1}} \sqrt{1+2\hat{G}_{2}\cdot \mathbf{E}\cdot\hat{G}_{2}}} =\frac{2 E_{12}}{\sqrt{1+2 E_{11}}\sqrt{1+2 E_{22}}}$ mit $\hat{G}_{1}=\frac{\mathrm{d}\vec{X}}{|\mathrm{d}\vec{X}|},\, \hat{G}_{2}=\frac{\mathrm{d}\vec{Y}}{|\mathrm{d}\vec{Y}|} \,.$

Der Tensor E ist der einheitenfreie Green-Lagrange’sche Verzerrungstensor, dessen Komponenten $E_{{ij}}$ sich auf das im Referenzzustand von den Vektoren $\hat{G}_{1,2}$ gebildete Basissystem beziehen, und „ $\cdot$ “ ist das Frobenius-Skalarprodukt von Vektoren. Die Komponente $E_{{12}}$ ist die Schubverzerrung in der 1-2-Ebene und $E_{{11}}$ sowie $E_{{22}}$ sind Normaldehnungen, die in der 1- und 2-Richtung auftreten.

Im Fall kleiner Verzerrungen geht der Green-Lagrange’sche Verzerrungstensor in den linearisierten Verzerrungstensor $\boldsymbol{\varepsilon}$ über, kann $\sin( \gamma) \approx \gamma$ und der Nenner im obigen Bruch gleich eins gesetzt werden mit dem Resultat

$\gamma\approx 2\hat{G}_{1}\cdot\boldsymbol{\varepsilon}\cdot\hat{G}_{2} =2\varepsilon_{12}=\frac{\partial u_1}{\partial X_2}+\frac{\partial u_2}{\partial X_1} \,.$

Die Komponenten beziehen sich auf ein kartesisches Koordinatensystem, das parallel zu den Vektoren $\hat{G}_{1,2}$ ausgerichtet ist, in dem X_1,2 die Koordinaten, u_1,2 die Verschiebungen und ε₁₂ die Schubverzerrung sind.

Die Schergeschwindigkeit berechnet sich im Zustand γ=0° mit dem Verzerrungsgeschwindigkeitstensor d aus^{[F
1]}

$\dot{\gamma}=2\hat{g}_1\cdot\mathbf{d}\cdot\hat{g}_2=2d_{12} =\frac{\partial v_1}{\partial x_2}+\frac{\partial v_2}{\partial x_1} \quad\text{mit}\quad \hat{g}_1=\frac{\mathrm{d}\vec{x}}{|\mathrm{d}\vec{x}|} \quad\text{und}\quad \hat{g}_2=\frac{\mathrm{d}\vec{y}}{|\mathrm{d}\vec{y}|} \,.$

Hier werden die zueinander orthogonalen Tangentenvektoren $\hat{g}_{1,2}$ also im deformierten Zustand ausgewählt. Die Komponenten beziehen sich auf ein kartesisches Koordinatensystem, das nun parallel zu den Vektoren $\hat{g}_{1,2}$ ausgerichtet ist, in dem x_1,2 die Koordinaten, v_1,2 die Geschwindigkeiten und d₁₂ die Schubverzerrungsgeschwindigkeit sind. Bei kleinen Verzerrungen ist $\mathbf{d}\approx\dot{\boldsymbol{\varepsilon}}$ und die Schergeschwindigkeit lautet:

$\dot{\gamma}\approx 2\hat{G}_1\cdot\dot{\boldsymbol{\varepsilon}}\cdot\hat{G}_2 =2\dot{\varepsilon}_{12} =\frac{\partial \dot{u}_1}{\partial X_2}+\frac{\partial \dot{u}_2}{\partial X_1} \approx\frac{\partial \dot{u}_1}{\partial x_2}+\frac{\partial \dot{u}_2}{\partial x_1} \,.$

Scherung in der Geologie

In der Geologie unterscheidet man zwischen den beiden Endgliedern reine Scherung (auch koaxiale Scherung oder reine Kompression) und einfache Scherung (auch nicht-koaxiale Scherung). Eine einfache Scherung beinhaltet im Vergleich zur reinen Scherung eine zusätzliche Rotationskomponente. Diese beiden Komponenten werden auch zur Diskussion von transpressiver (Kompression plus Lateralbewegung) und transtensiver (Extension plus Lateralbewegung) Tektonik gebraucht.

Dynamik der Scherung von Festkörpern

Eine Schubbelastung ist eine Kraft oder ein Moment, bei der der belastete Körper zumindest lokal eine Scherbewegung ausführt. Diese äußere Belastung setzt sich im Körper in Spannungen, insbesondere Schubspannungen, um. Scherbelastung tritt nicht nur bei äußerer Belastung auf, sondern zum Beispiel auch

bei thermischer Belastung von miteinander flächig verbundenen Körpern, die unterschiedliche Wärmeausdehnungskoeffizienten besitzen,
aufgrund latenter Spannungen bei inhomogener Erstarrung, zum Beispiel beim Schweißen, oder
bei Beschichtungen, die nach der Aufbringung anders schrumpfen als das Grundmaterial.

Bei der Scherung – oder allgemein bei einer Schubbelastung – steht die Schubspannung τ und die Schubverzerrung oder Gleitung γ im geometrisch linearen Bereich und bei linearer Elastizität in der Beziehung

$\tau = G\gamma\,.$

Die Proportionalitätskonstante G ist der Schubmodul (auch: Scher- oder Gleitmodul). Die Schubspannung wird bei der Scherung auch Scherspannung genannt und hat – wie der Schubmodul – die Dimension Kraft pro Fläche. Die SI-Einheit ist damit das Pascal (Pa), also N/m² – Newton pro Quadratmeter.

Lokal werden bei einer Scherung im elastischen Bereich im Körper materielle Flächen relativ zueinander, reversibel, parallel verschoben. Die Fläche kann sich dabei verwölben, wie es beispielsweise bei der Torsion eines nicht kreisrunden Stabes oder der Querkraftbelastung eines Trägers passiert. Bei Überschreitung der Scherfestigkeit wird das Werkstück abgeschert (siehe die Beispiele zum Torsionsbruch). Außerhalb des elastischen Bereichs bis zum Erreichen der Scherfestigkeit verformen sich duktile Materialien plastisch, worauf im Folgenden eingegangen wird.

Scherung kristalliner Werkstoffe

Übersteigt die Scherbelastung die Elastizitätsgrenze kommt es in duktilen kristallinen Werkstoffen – insbesondere Metallen – zu Versetzungsbewegungen. In einem kristallinen Werkstoff werden bei der Scherung Kristallteile gegeneinander verschoben. Die Ebene, die die Kristallteile voneinander trennt, ist die Gleitebene, die gemeinsam mit der Gleitrichtung das Gleitsystem bildet. Im Beispiel mit dem Buch wären die Gleitebenen die Buchseiten, die nun in der Gleitrichtung senkrecht zum Buchrücken in der Papierebene aufeinander abgleiten. Ist ${\vec {n}}$ der Normalenvektor der Gleitebene und ${\vec m}$ die Gleitrichtung in der Ebene, dann ist die Schubspannung im Gleitsystem (GS) durch den Spannungstensor ${\boldsymbol {\sigma }}$ gegeben:

$\tau^{(GS)}=\vec{n}\cdot\boldsymbol{\sigma}\cdot\vec{m} \quad\text{mit}\quad \vec m\cdot\vec n=0\,.$

Wird die kritische Schubspannung $\tau_\text{krit}$ von der Schubspannung $\tau^{(GS)}$ im Gleitsystem überschritten, gleiten die Atome beiderseits der Gleitebene aneinander ab und es kommt zu plastischer Verformung.

Scherung polykristalliner Werkstoffe

In polykristallinen, isotropen Werkstoffen wechselt die Kristallorientierung mit den Kristallkörnern, deren Verformungen sich gegenseitig behindern können, wodurch die Schubfließgrenze $\sigma _{F}$ ansteigt. Der Zusammenhang zwischen der Schubfließgrenze und der kritischen Schubspannung ist der Taylor-Faktor M:

$\sigma_F=M \tau_\text{krit}\,.$

Bei kubisch flächenzentriertem Gitter ist M=3,1 und bei kubisch raumzentriertem Gitter ist M=2,9. Der Taylor-Faktor berechnet sich aus den statistischen Eigenschaften der Kristallkörner im Polykristall.

Scherung von Thermoplasten

Thermoplaste können sich plastisch verformen, indem sich die Kettenmoleküle, aus denen sie bestehen, lokal strecken. Dadurch entstehen – insbesondere unter Druck – Scherbänder, die in einem Winkel von 45° bis 60° zur Belastungsrichtung orientiert sind, wo lokalisiert große plastische Verformungen von 100 % und mehr auftreten, abseits von denen die Verformungen aber gering sind.

Scherung von Fluiden

Ausbildung einer laminaren Grenzschicht zwischen der blauen Linie und einer flachen Oberfläche (untere Linie).

Scherung ist auch in Fluiden bedeutsam, und die Schergeschwindigkeiten in ihnen berechnen sich wie im Abschnitt zur Kinematik geschildert. In reibungsfreien Flüssigkeiten und Gasen führen die Schergeschwindigkeiten allerdings nicht zu Schubspannungen. Die in der Strömungsmechanik zumeist betrachteten Fluide, sind die Newton’schen Fluide, deren Geschwindigkeitsfeld den Navier-Stokes-Gleichungen gehorcht. Das Materialmodell für das Newton’sche Fluid lautet:

${\boldsymbol {\sigma }}=-p(\rho )\mathbf {1} +2\mu \mathbf {d} +\lambda \operatorname {Sp} (\mathbf {d} )\mathbf {1} \,.$

Darin sind p der im Allgemeinen von der Dichte ρ abhängige Druck, λ und μ die ersten und zweiten Lamé-Konstanten, Sp die Spur und 1 der Einheitstensor. Die Schubspannungen sind also mit $2\mu \mathbf{d}$ proportional zum oben genannten Verzerrungsgeschwindigkeitstensor, was sich makroskopisch als Viskosität bemerkbar macht.

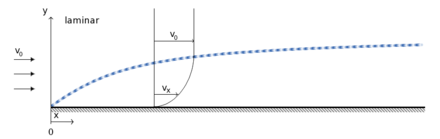
An Wänden, wo die Haftbedingung keine wandparallele Bewegung des Fluids an der Wand zulässt, führt die Schubspannung zur Ausbildung einer Grenzschicht, in der sich die Geschwindigkeit an die Geschwindigkeit im Hauptstrom angleicht, siehe Bild. Strömt das Fluid in x-Richtung parallel zur Wand und weist die Wandnormale in y-Richtung, dann lautet die Schubspannung im Abstand von einer ebenen Wand:

$\tau(y) =\mu\dot{\gamma}_{xy} =2\mu\hat{g}_x\cdot\mathbf{d}\cdot\hat{g}_y =\mu \left(\frac{\partial v_x}{\partial y}+\frac{\partial v_y}{\partial x}\right) =\mu \frac{\partial v_x}{\partial y} \,,$

denn der Term mit der Geschwindigkeit $v_{y}$ senkrecht zur Wand kann hier vernachlässigt werden. Insbesondere ist die Wandschubspannung definiert durch

$\tau_w:=\tau(y=0)=\left.\mu \frac{\partial v_x}{\partial y}\right|_{y=0}\,.$

Nicht-newtonsche Fluide zeigen eine nicht-lineare Abhängigkeit der Schubspannungen von den Schergeschwindigkeiten.

Beispiel

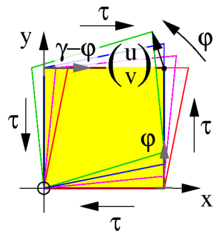
Scherung eines Quadrats (gelb) in Parallelogramme

In der x-y-Ebene erfahren die Punkte eines Einheitsquadrats mit $(x,y)\in[0,1]\times[0,1]$ die Verschiebung

$\vec u :=\begin{pmatrix} u\\v \end{pmatrix} :=\begin{pmatrix} \left(\gamma-\varphi\right) y \\ \varphi x \end{pmatrix}\,.$

Der Parameter γ ist die Gleitung und φ bewirkt eine Drehung. Aus Ableitungen nach dem Ort berechnet sich der linearisierte Verzerrungstensor

$\boldsymbol{\varepsilon} =\begin{pmatrix} \frac{\partial u}{\partial x} & \frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) \\ \frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) & \frac{\partial v}{\partial y} \end{pmatrix} =\frac{1}{2}\begin{pmatrix} 0 &\gamma-\varphi+\varphi\\ \gamma-\varphi+\varphi & 0 \end{pmatrix} =\frac{1}{2}\begin{pmatrix} 0 & \gamma \\ \gamma & 0 \end{pmatrix}$

der – anders als im Bild – nur zulässig ist bei $|\gamma|,\,|\varphi|\ll10^\circ\,.$ Mit dem Hooke’schen Gesetz ergibt sich der Spannungstensor

${\boldsymbol {\sigma }}=2G{\boldsymbol {\varepsilon }}+\lambda \operatorname {Sp} ({\boldsymbol {\varepsilon }})\mathbf {1} =2G{\boldsymbol {\varepsilon }}=G{\begin{pmatrix}0&\gamma \\\gamma &0\end{pmatrix}}={\begin{pmatrix}0&\tau \\\tau &0\end{pmatrix}}\,,$

in Abhängigkeit vom Schubmodul G und der ersten Lamé-Konstanten λ. Der Operator Sp bildet die Summe der Diagonalelemente (Spur) und $\mathbf{1}$ ist der Einheitstensor. Die Schubspannungen haben die Größe $\tau=G\gamma\,.$ Der Verzerrungs- und Spannungstensor besitzen hier – im Rahmen der geometrisch linearen Betrachtung – keine Normalkomponenten.

In Schnittebenen mit Normalenvektoren

$\hat{n}_{1,2}:=\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\\pm 1 \end{pmatrix}$

treten keine Schubspannungen auf, weil die Schnittspannungsvektoren $\vec{t}_{1,2}:=\boldsymbol{\sigma}\cdot\hat{n}_{1,2}=\pm\tau\hat{n}_{1,2}$ genau in Normalenrichtung weisen ( $\pm\tau$ sind Hauptspannungen und $\hat{n}_{1,2}$ sind die dazugehörenden Hauptspannungsrichtungen.)

Der linearisierte Verzerrungstensor ist der symmetrische Anteil des Verschiebungsgradienten

$\mathbf{H} :=\begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{pmatrix} =\begin{pmatrix} 0 & \gamma-\varphi \\ \varphi & 0 \end{pmatrix} \,.$

Durch Addition des nicht linearen Anteils

$\mathbf{H^\top\cdot H} = \begin{pmatrix} 0 & \varphi \\ \gamma-\varphi & 0 \end{pmatrix} \cdot\begin{pmatrix} 0 & \gamma-\varphi \\ \varphi & 0 \end{pmatrix} = \begin{pmatrix} \varphi^2 & 0 \\ 0 & (\gamma-\varphi)^2 \end{pmatrix}$

zum linearisierten Verzerrungstensor ergibt sich der Green-Lagrange’sche Verzerrungstensor

$\mathbf{E} =\frac{1}{2}(\mathbf{H+H^\top+H^\top\cdot H}) =\frac{1}{2}\begin{pmatrix} \varphi^2 & \gamma \\\gamma & (\gamma-\varphi)^2 \end{pmatrix} \,.$

Bei der Scherung eines Quadrats zu einem flächengleichen Parallelogramm treten deshalb bei großer Scherbewegung Normaldehnungen auf.

Anmerkungen

↑ Die Groß- und Kleinschreibung der Variablen ist zu beachten. Variablen in Großbuchstaben beziehen sich auf den Referenzzustand und solche in Kleinbuchstaben auf den aktuellen Zustand, der gegenüber dem Referenzzustand stark deformiert und verdreht sein kann.

Siehe auch

Festkörper:

Schmidsches Schubspannungsgesetz

Fluide:

Literatur

H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 3. Auflage. Springer-Vieweg, 2008, ISBN 978-3-642-40980-6.
H. Altenbach: Kontinuumsmechanik: Einführung in die materialunabhängigen und materialabhängigen Gleichungen. Springer, 2012, ISBN 3-642-24119-0.

Basierend auf einem Artikel in:

Wikipedia.de