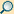Vergleichsspannung
Die Vergleichsspannung ist ein Begriff aus der Festigkeitslehre. Dieser bezeichnet eine fiktive einachsige Spannung, die aufgrund eines bestimmten werkstoffmechanischen bzw. mathematischen Kriteriums eine hypothetisch gleichwertige Materialbeanspruchung darstellt wie ein realer, mehrachsiger Spannungszustand.
Anhand der Vergleichsspannung kann der wirkliche, i. A. dreidimensionale Spannungszustand im Bauteil in der Festigkeits- oder in der Fließbedingung mit den Kennwerten aus dem einachsigen Zugversuch (Material-Kennwerte, z.B. Streckgrenze oder Zugfestigkeit) verglichen werden.
Grundlagen
Zur vollständigen Beschreibung des Spannungszustandes in einem Bauteil ist im Allgemeinen die Angabe des Spannungstensors (Tensor 2. Stufe) notwendig. Dieser enthält im allgemeinen Fall (Kräfte- und Momentengleichgewicht) sechs verschiedene Spannungswerte (da einander zugeordnete Schubspannungen gleich sind). Durch die Transformation des Spannungstensors in ein ausgezeichnetes Koordinatensystem (das Hauptachsensystem) werden die Schubspannungen zu Null und drei ausgezeichnete (Normal)Spannungen (die Hauptspannungen) beschreiben den Beanspruchungszustand des Systems äquivalent.
Die Elemente des Vektors der Hauptspannungen bzw. des Spannungstensors können nun in einen Skalar überführt werden, der zwei Bedingungen genügen soll:
- zum einen soll er den Spannungszustand möglichst umfassend beschreiben (Äquivalenz kann hier nicht mehr erreicht werden: es treten immer Informationsverluste beim Übergang vom Vektor der Hauptspannungen zur Vergleichsspannung auf)
- zum anderen soll er auf jeden Fall eine versagensrelevante Information darstellen.
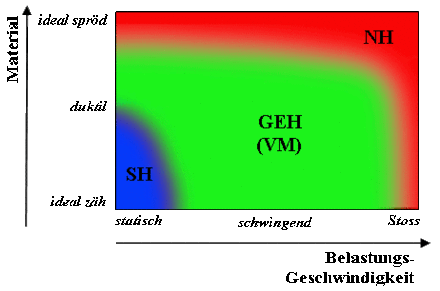
Die Rechenvorschrift zur Bildung dieser skalaren Vergleichsspannung bezeichnet man als Vergleichspannungshypothese bzw. als Versagensregel. Im Rahmen einer Tragfähigkeitsanalyse vergleicht man die Vergleichsspannung mit zulässigen Spannungen. Durch die Wahl der Hypothese enthält sie implizit den Versagensmechanismus und ist damit ein Wert, der die Gefährdung des Bauteils unter der gegebenen Beanspruchung ausdrückt. Die Wahl der jeweiligen Vergleichspannungshypothese hängt also immer vom Festigkeitsverhalten des nachzuweisenden Materials sowie vom Lastfall (statisch, schwingend, Stoß) ab.
Es gibt eine ganze Anzahl von Hypothesen zur Berechnung der Vergleichsspannung. Sie werden in der Technischen Mechanik häufig unter dem Begriff Festigkeitshypothesen zusammengefasst. Die Anwendung hängt vom Materialverhalten und teilweise auch vom Anwendungsgebiet (wenn etwa eine Norm die Anwendung einer bestimmten Hypothese fordert) ab.
Am häufigsten wird im Maschinenbau und im Bauwesen die Gestaltänderungsenergiehypothese nach Richard von Mises angewendet. Außer den hier genannten gibt es noch weitere Hypothesen.
Gestaltänderungshypothese (von Mises)
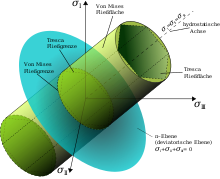
Nach der Gestaltänderungshypothese, auch Gestaltänderungsenergiehypothese (kurz: GEH) oder Mises-Vergleichsspannung nach Richard von Mises genannt, tritt Versagen des Bauteils dann auf, wenn die Gestaltänderungsenergie einen Grenzwert überschreitet (s. auch Verzerrungen bzw. Deformation). Verwendet wird diese Hypothese für zähe Werkstoffe (z.B. Stahl) unter ruhender und wechselnder Beanspruchung. Die Mises-Vergleichsspannung wird im Maschinenbau und im Bauwesen am häufigsten eingesetzt -- für die meisten gängigen Materialien (nicht allzu spröde) unter normaler Belastung (wechselnd, nicht stoßartig) ist die GEH einsetzbar. Wichtige Anwendungsgebiete sind die Berechnungen von Wellen, die sowohl auf Biegung als auch auf Torsion beansprucht werden, sowie der Stahlbau. Die GEH ist so konstruiert, dass sich bei hydrostatischen Spannungszuständen (gleich große Spannungen in allen drei Raumrichtungen), eine Vergleichsspannung von Null ergibt. Denn plastisches Fließen von Metallen ist isochor und selbst extreme hydrostatische Drücke haben keinen Einfluss auf den Fließbeginn (Experimente von Bridgman).
Beschreibung im allgemeinen Spannungszustand:
andere Schreibweise:
Beschreibung im Hauptspannungszustand:
,
und
sind die Hauptspannungen.
Beschreibung im ebenen Spannungszustand:
Beschreibung im ebenen Verzerrungszustand mit:
Beschreibung in Invariantendarstellung:
wobei
die zweite Invariante des Spannungsdeviators
ist:
Schubspannungshypothese (Tresca, Coulomb, Saint-Venant, Guest)
Es wird davon ausgegangen, dass für das Versagen des Werkstoffes die größte
Hauptspannungsdifferenz verantwortlich ist (Bezeichnung in einigen FE-Programmen:
Intensität). Diese Hauptspannungsdifferenz entspricht dem doppelten Wert der
maximalen Schubspannung
– dadurch wird sie bei zähem
Material unter statischer Belastung, welches durch Fließen (Gleitbruch)
versagt, angewandt. Im Mohr’schen
Spannungskreis ist die kritische Größe der Durchmesser des größten Kreises.
Die Schubspannungshypothese findet aber auch im Maschinenbau
ganz allgemein Anwendung, da der Formelapparat
im Vergleich zur GEH einfacher zu handhaben ist und man mit ihr im Vergleich zu
Von Mises (GEH) auf der sicheren Seite liegt (es kommen im Zweifelsfall etwas
größere Werte für die Vergleichsspannung und damit auch etwas mehr
Sicherheitsreserven heraus).
Räumlicher Spannungszustand:
,
und
sind die Hauptspannungen.
Ebener Spannungszustand (vorausgesetzt
und
haben unterschiedliche Vorzeichen):
Hauptnormalspannungshypothese (Rankine)
Es wird davon ausgegangen, dass das Bauteil aufgrund der größten Normalspannung versagt. Im Mohr'schen Spannungskreis ist der kritische Punkt die maximale Hauptspannung. Die Hypothese wird angewendet für Werkstoffe, welche mit Trennbruch, ohne Fließen, versagen:
- spröde Werkstoffe (z.B. Grauguss oder Schweißnähte) bei vorwiegend ruhender Zugbeanspruchung
- spröde und zähe Materialien bei stoßartiger Belastung.
Räumlicher Spannungszustand:
für
ansonsten
für
Ebener Spannungszustand:
Quadratisches rotationssymmetrisches Kriterium (Burzyński-Yagn)
Mit dem Ansatz
folgen die Kriterien:
- Konus von Drucker-Prager (Mirolyubov) mit ,
- Paraboloid von Balandin (Burzyński-Torre) mit ,
- Ellipsoid von Beltrami mit ,
- Ellipsoid von Schleicher mit ,
- Hyperboloid von Burzyński-Yagn mit ,
- einschaliges Hyperboloid.
Die quadratischen Kriterien lassen sich explizit nach
auflösen, was ihren praktischen Einsatz förderte.
Die Querkontraktionszahl bei Zug lässt sich mit
berechnen. Die Anwendung von rotationssymmetrischen Kriterien für sprödes Versagen
wurde nicht genügend untersucht.
Kombiniertes rotationssymmetrisches Kriterium (Huber)
Das Kriterium von Huber besteht aus dem Ellipsoid von Beltrami
für
und einem zu ihm im Schnitt
gekoppelten Zylinder
für
mit dem Parameter .
Der Übergang im Schnitt
ist stetig-differenzierbar. Die Querkontraktionszahlen bei Zug und Druck ergeben
sich zu
Das Kriterium wurde 1904 entwickelt. Es setzte sich jedoch zunächst nicht durch, da es von mehreren Wissenschaftler als unstetiges Modell verstanden wurde.
Unified Strength Theory (Mao-Hong Yu)
Die Unified Strength Theory (UST) die um 60° gegeneinander gedreht sind:
mit
und
.
Mit
ergibt sich das Kriterium von Mohr-Coulomb (Single-Shear Theorie von Yu), mit
das Pisarenko-Lebedev Kriterium und mit
folgt die Twin-Shear Theorie von Yu (vgl. Pyramide von Haythornthwaite).
Die Querkontraktionszahlen beim Zug und beim Druck folgen als
Cosinus Ansatz (Altenbach-Bolchoun-Kolupaev)
Oft werden die Festigkeitshypothesen unter Verwendung des Spannungswinkels
formuliert. Mehrere Kriterien isotropen Materialverhaltens werden im Ansatz
zusammengefasst.
Die Parameter
und
beschreiben die Geometrie der Fläche in der
-Ebene.
Sie müssen die Bedingungen
erfüllen, welche sich aus der Konvexitätsanforderung ergeben.
Die Parameter
und
beschreiben die Lage der Schnittpunkte der Fließfläche mit der hydrostatischen
Achse (Raumdiagonale im Hauptspannungsraum). Diese Schnittpunkte werden
hydrostatische Knoten genannt. Für die Materialien, die unter der gleichmäßigen
3D-Druckbelastung nicht versagen (Stahl, Messing usw.), ergibt sich
.
Für die Materialien, die unter dem gleichmäßigen 3D-Druck versagen (harte
Schäume, Keramiken, gesinterte Materialien), gilt
.
Die ganzzahligen Potenzen
und
,
beschreiben die Krümmung des Meridians. Der Meridian ist mit
eine Gerade und mit
eine Parabel.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.04. 2024