Streckgrenze
Die Streckgrenze
(englisch yield strength,
)
ist eine Werkstoffkenngröße
und bezeichnet diejenige mechanische
Spannung, bis zu der ein Werkstoff
elastisch
verformbar ist. Die
Streckgrenze bezeichnet den Spezialfall der Elastizitätsgrenze
bei einachsiger und momentenfreier
Zugbeanspruchung. Aufgrund
der leichteren Messbarkeit kommt der Streckgrenze die größere technische
Bedeutung zu.
- bei Unterschreiten der Streckgrenze kehrt das Material nach Entlastung elastisch in seine ursprüngliche Form zurück
- bei Überschreiten der Streckgrenze verbleibt eine plastische Formveränderung, bei einer Zugprobe also eine Dehnung.
Bei vielen Werkstoffen ist die Streckgrenze im Zugversuch nicht eindeutig identifizierbar bzw. nicht ausgeprägt, weshalb stattdessen z. B. die 0,2-%-Dehngrenze verwendet wird.
Messung
Die Streckgrenze ist mittels Zugversuch zu ermitteln.
Aus der Streckgrenze und der ebenfalls im Zugversuch ermittelten Zugfestigkeit
lässt sich das Streckgrenzenverhältnis errechnen:
Dieses gibt dem Konstrukteur Auskunft über den Abstand zwischen einsetzender plastischer Deformation und Versagen des Werkstoffes bei quasistatischer Beanspruchung. Der Wert spielt etwa bei Schraubverbindungen eine wichtige Rolle, wo im Allgemeinen ein höherer Wert erwünscht ist, da eine bleibende Dehnung nach einer Belastung ein Lösen der Schraube bedeuten würde.
Dehngrenze (= Ersatzstreckgrenze)
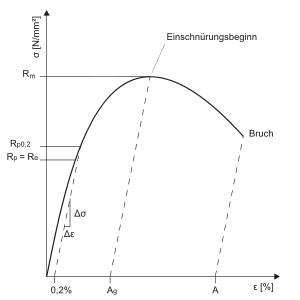
Bei technischen Werkstoffen wird statt der Streckgrenze in der Regel die
0,2-%-Dehngrenze
oder Elastizitätsgrenze
angegeben, da sie (im Gegensatz zur Streckgrenze) immer eindeutig aus dem Nennspannungs-Totaldehnungs-Diagramm
ermittelt werden kann (oft ist eigentlich die Dehngrenze gemeint, wenn die
Streckgrenze angegeben wird). Die 0,2-%-Dehngrenze ist diejenige (einachsige) mechanische
Spannung, bei der die auf die Anfangslänge der Probe bezogene bleibende Dehnung
(d.h. plastische Dehnung, daher der Index
)
nach Entlastung 0,2 % beträgt. Bei sehr duktilen Werkstoffen, wie
vielen Kunststoffen, kann aufgrund
von Viskoplastizität
eine 0,2-%-Dehngrenze nur ungenau bestimmt werden und es wird stattdessen eine
2-%-Dehngrenze angegeben.
Bei höherer Last kommt es entweder zu weiteren plastischen Verformungen, oder bei Werkstoffen mit hoher Sprödigkeit wird die Zugfestigkeit überschritten und es kommt zum Bruch.
| Werkstoffgruppe | Legierung | 0,2-%-Dehngrenze in MPa |
|---|---|---|
| Kupfer-Legierungen (ungefähre Werte) | E-Cu57 | 160 |
| CuZn37 | 250…340 | |
| CuZn39Pb3 | 250…340 | |
| CuNi1, 5Si | 540 | |
| Magnesium-Legierungen (ungefähre Werte) | CP Mg | 40 |
| AZ91 | 110 | |
| AM60 | 130 | |
| WE54 | 200 | |
| MgZn6Zr | 250 | |
| Aluminium-Legierungen (ungefähre Werte) | Al99.5 | 40 |
| AlMg1 | 100 | |
| AlMg3 | 120 | |
| AlMg4.5Mn | 150 | |
| AlMgSi0.5 | 190 | |
| AlCu4PbMgMn | 220…250 | |
| AlZnMgCu1.5 | 450 | |
| AA 7175 | 525 | |
| Titan-Legierungen (ungefähre Werte) | CP Ti | 220 |
| Ti-6Al-4V | 924 | |
| Ti-6Al-2Fe-0.1Si | 960 | |
| Ti-15Mo-3Nb-3Al-.2Si | 1400 | |
| Baustähle | S235JR | 235 |
| S275 | 275 | |
| S355 | 355 | |
| E360 | 360 | |
| Nichtrostende Stähle (typische Werte) | WNr. 1.4301 | 190 |
| WNr. 1.4307 | 175 | |
| Betonstähle | BSt 420 | 420 |
| BSt 500 | 500 | |
| BSt 550 | 550 | |
| Spannstähle | St 1370/1570 | 1370 |
| St 1570/1770 | 1570 | |
| Vergütungsstähle | C22 | 340 |
| C45 | 490 | |
| C60 | 580 | |
| 42CrMo4 | 900 | |
| 34CrNiMo6 | 1000 | |
| Einsatzstähle | C10E | 430 |
| 16MnCr5 | 630 | |
| 18CrNiMo7-6 | 685 |
Beispiel „Bergseil“
Wird beispielsweise ein Kletterseil aus Polyamid („Nylon“) auf Zug belastet, so dehnt es sich zuerst um etwa 10 %. Wird es entlastet, so verkürzt es sich wieder bis auf seine ursprüngliche Länge (elastische Dehnung unterhalb der Streckgrenze).
Wird das Seil stärker belastet und dehnt es sich über die Streckgrenze hinaus, dann verkürzt es sich auch nach Entlastung nicht mehr ganz.
Wird es noch stärker belastet, so wird irgendwann die Fließgrenze überschritten. Dann beginnt das Material trotz gleichbleibender Krafteinwirkung sich zu verändern, es fließt (= Umlagerung der Molekülketten).
Ausgeprägte Streckgrenze
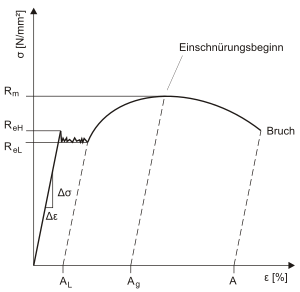
Durch Fremdatomwolken, auch Cottrellwolken, die sich bevorzugt in energetisch günstigen Verzerrungsfeldern um Versetzungen aufhalten, kann es zur Ausbildung ausgeprägter Streckgrenzen kommen. Vor allem folgende Streckgrenzeneffekte treten auf:
Obere Streckgrenze
Die obere Streckgrenze
(Index
= engl. high = hoch, oben) wird durch Losreißprozesse von Versetzungen
verursacht, die die interstitiellen
Fremdatomwolken verlassen. Im Anschluss daran fällt die Spannung im Werkstoff
auf die untere Streckgrenze, und die Verformung wird mit der Lüdersdehnung
fortgesetzt.
Dieser Effekt tritt ausschließlich bei unlegierten Stählen mit niedrigem Kohlenstoffgehalt auf.
Untere Streckgrenze
Die untere Streckgrenze
(Index
= engl. low = niedrig, unten) ist die Folge des Losreißens von
Versetzungen bei
von Cottrellwolken. Diese Versetzungen können nun mit deutlich geringerer
Energie bewegt werden, da sich die Fremdatomwolken nicht mehr im
Verzerrungsbereich der Versetzungen befinden. Dieser Effekt ist eine Folge des
Auftretens einer oberen Streckgrenze und gleichzeitig die Nennspannung, bei der
die Lüdersdehnung stattfindet.
Lüdersdehnung
Als Lüdersdehnung εL (nach Klaus Lüders) wird ein plastischer Dehnungsanteil bezeichnet, der durch die Bewegung einer Versetzungsfront durch ein Bauteil oder eine Probe bei konstanter Beanspruchung gekennzeichnet ist. Während der Lüdersverformung bleibt dabei die Nennspannung (und damit die anliegende Kraft) nahezu konstant bei der unteren Streckgrenze. Die Lüdersfront wird in der Regel an einer lokalen Spannungsüberhöhung (Kerbe, Oberflächenrauhigkeit, Querschnittsübergang) ausgelöst und bewegt sich dann durch die gesamte Probenmessstrecke bzw. bis zu einer deutlichen Querschnittsvergrößerung. Die an der Oberfläche eines Bauteils sichtbaren Verformungslinien werden als Lüdersbänder oder Fließfiguren bezeichnet.
Dieser Effekt tritt bei un- und niedriglegierten untereutektoiden Stählen auf, aber auch in Kupfer- und Aluminiumlegierungen, und ist unabhängig vom Auftreten einer oberen Streckgrenze.
Wird eine Probe einmal über den Bereich der Lüdersdehnung hinaus gestreckt, dann tritt bei einem zeitnahen Wiederholen der Probenverformung kein Streckgrenzeneffekt bzw. keine Lüdersdehnung mehr auf, da sich die Versetzungen von den Fremdatomwolken bereits losgerissen haben. Aus diesem Grund werden Tiefziehbleche im Vorfeld häufig kaltgewalzt, um die Bildung von Fließfiguren während des eigentlichen Tiefziehens zu verhindern.
Literatur
- Winfried Dahl: Mechanische Eigenschaften. In: Verein Deutscher Eisenhüttenleute (Hrsg.): Werkstoffkunde Stahl. Band 1: Grundlagen. Springer-Verlag, Berlin/ Heidelberg/ New York/ Tokyo; Verlag Stahleisen, Düsseldorf 1984.
- Klaus Lüders, Gebhard von Oppen: Bergmann Schaefer: Lehrbuch der Experimentalphysik. Band 1: Mechanik, Akustik, Wärme. 12., völlig neu bearb. Auflage. de Gruyter, 2008.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.04. 2024