Plastizität (Physik)

Die Plastizität oder plastische Verformbarkeit (in Kunst und Kunsthandwerk auch Bildsamkeit) beschreibt die Fähigkeit von Feststoffen, sich unter einer Krafteinwirkung nach Überschreiten einer Elastizitätsgrenze irreversibel zu verformen bzw. umzuformen (zu fließen) und diese Form nach der Einwirkung beizubehalten. Unterhalb der Fließgrenze treten keine oder nur elastische Deformationen auf. In der Praxis treten diese Effekte aber immer gemeinsam auf.

Duktilität wird auch synonym zu Plastizität gebraucht, womit diese Begriffe nicht immer eindeutig voneinander abgegrenzt werden können.

Materialverhalten

Siehe auch: „Ideale Plastizität“ im Artikel Rheologisches Modell

Ein ideal plastischer Körper verhält sich wie ein starrer, nicht deformierbarer Festkörper, solange die einwirkende Spannung $\sigma$ unterhalb der Fließgrenze $\sigma _{F}$ bleibt. Erreicht $\sigma$ den Wert $\sigma _{F}$ , beginnt er sich irreversibel und unbegrenzt zu verformen. Ideal plastisches Verhalten tritt in der Natur aber praktisch nicht auf, sondern stets gemeinsam mit elastischen oder viskosen Effekten. Beispielsweise verhält sich Stahl im Zugversuch elastoplastisch. Demgegenüber weisen die Bingham-Fluide ein viskoplastisches Verhalten auf. Sie verhalten sich unterhalb einer Fließgrenze wie ein Festkörper und darüber wie eine Flüssigkeit.

Fließt ein Stoff unter Krafteinwirkung sofort, nicht erst nach Überschreiten einer Fließgrenze, so handelt es sich nicht um einen Feststoff, sondern um eine viskose Flüssigkeit.

Im Gegensatz dazu würde ein elastischer Stoff seine ursprüngliche Form wieder einnehmen und ein spröder Stoff mit sofortigem Versagen reagieren – man spricht von Sprödbruch, der z.B. bei Keramiken und kubisch-raumzentrierten Metallen bei tiefen Temperaturen auftritt.

Beschreibung

St.-Venant-Element

Der Grad der Dehnung $\varepsilon$ kann als normierte Längenänderung des Körpers angegeben werden. Gebräuchlicher ist jedoch der Umformgrad $\varphi$ .

Häufig verwendete Modelle für die Berechnung und Simulation der Fließspannungen aus einem Spannungstensor wurden von Tresca oder von Mises formuliert.

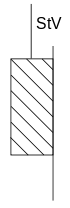
Das Verhalten eines ideal plastischer Körpers kann durch ein St.-Venant-Element modelliert werden, einem Reibklotz, der sich erst nach Überschreiten einer bestimmten Haftreibungskraft in Bewegung setzt.

Ein Modell zur mathematischen Beschreibung der Plastizität stammt von Eugene C. Bingham. Dieses wird vor allem bei Finite-Elemente-Berechnungen der Viskoplastizität von Materialien wie Ziegelrohmassen verwendet. In der Kontinuumsmechanik befasst sich die Plastizitätstheorie mit der irreversiblen Umformung von Materie.

Ursachen

Das plastische Verformungsverhalten hängt unter anderem vom Spannungszustand, der Temperatur, der Belastungsart und der Belastungsgeschwindigkeit ab. So kennt man neben der herkömmlichen Plastizität auch die Hochtemperaturplastizität, Kriechverformung und Superplastizität. Innerhalb des Materials ist die plastische Verformung eine Folge von Scherspannungen zwischen den Molekülen und Atomen.

Kristalline Festkörper

Mikroskopisch wird die plastische Verformung von kristallinen Festkörpern (Metallen) anhand der Versetzungstheorie beschrieben. Es ist eine geringere Scherkraft erforderlich, um eine plastische Verformung hervorzurufen, indem einzelne Defekte (Versetzungen) durch den Festkörper wandern, als sämtliche Atomreihen gleichzeitig zu bewegen. Als Analogie wird oft ein großer Teppich betrachtet, der nur um ein kleines Stück verschoben werden soll. Dies ist sehr kraftsparend möglich, indem eine kleine Falte durch den Teppich getrieben wird, statt den gesamten Teppich auf einmal zu verschieben. (Siehe auch Festigkeit)

Technische Bedeutung

Hinsichtlich der technischen Eigenschaften eines Materials kann die Plastizität je nach Kraftangriff unterteilt werden in

Duktilität (engl. ductility): das plastische Verhalten unter Zugspannung (Tension)
Schmiedbarkeit (engl. malleability): das plastische Verhalten unter Druckspannung (Kompression).

Die Plastizität bestimmt die Duktilität und Umformbarkeit eines Werkstoffes.

Beispiele

Hohe Plastizität:

Knete
feuchter Ton
Metalle und Metalllegierungen mit geeignetem Atomgitter:
- glühender Stahl beim Schmieden
- Kaltumformung von Blechen beim Treiben
- einen dünnen Metalldraht kann man in jede beliebige Form biegen
typische Bingham-Fluide wie Zahnpasta, Mayonnaise oder Butter kann man schon mit geringem Druck auf die Tube oder mit dem Messer erweichen und zum Fließen bringen.
Bei sehr hohem Druck wird Eis plastisch und kann als Gletscher fließen.
Bei noch höheren Drücken wird Halit (Steinsalz) ebenfalls plastisch und kann Salzstöcke und sogar Salzgletscher bilden.

Geringe Plastizität:

Ein Gummiband ist sehr elastisch und kehrt daher nach Lastrücknahme zu seiner ursprünglichen Form zurück.
Keramiken brechen meist spröde ohne plastische Verformung.

Literatur

E. C. Bingham, Fluidity and Plasticity. McGraw-Hill, New York 1922
W. F. Hosford, The mechanics of crystals and textured polycrystals. Oxford University Press, 1993
Gustav E. R. Schulze, Metallphysik – ein Lehrbuch. Akademie-Verlag, Berlin 1967

Basierend auf einem Artikel in:

Wikipedia.de