Technische Mechanik

Teilgebiete der Technischen Mechanik

Die Technische Mechanik ist ein Teil der Mechanik. Sie wendet die physikalischen Grundlagen auf technische Systeme an und behandelt vor allem die in der Technik wichtigen festen Körper. Ziel ist vor allem die Berechnung der in den Körpern wirkenden Kräfte. Vorlesungen in Technischer Mechanik sind fester Bestandteil in den Studiengängen des Maschinenbaus und des Bauingenieurwesens. Außerdem wird sie in weiteren Ingenieurwissenschaften behandelt wie der Elektrotechnik, dem Industriedesign oder dem Wirtschaftsingenieurwesen.

Das Aufgabengebiet der Technischen Mechanik ist die Bereitstellung der theoretischen Berechnungsverfahren beispielsweise für den Maschinenbau und die Baustatik. Die eigentliche Bemessung der Bauteile oder Tragwerke, die Auswahl der Werkstoffe und dergleichen wird dann von anwendungsnahen Disziplinen übernommen, in denen die Technische Mechanik Hilfswissenschaft ist, beispielsweise die Konstruktionslehre oder die Betriebsfestigkeit.

Gegenstände der Technischen Mechanik sind

die Gesetze der klassischen Mechanik,
mathematische Modelle der mechanischen Zusammenhänge physischer Körper,
spezifische und rationelle Methoden der rechnerischen Analyse mechanischer Systeme.

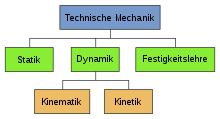
Die klassische Einteilung erfolgt in

die Statik, die sich mit Kräften auf ruhende (unbewegte) Körper (hauptsächlich mit eindimensionalen Stäben) befasst,
die Festigkeitslehre, die sich mit deformierbaren Körpern (bzw. hauptsächlich Querschnitten) befasst und Material- und Querschnittseigenschaften integriert,
die Dynamik mit den beiden Teilgebieten Kinetik und Kinematik, die sich mit bewegten Körpern befassen.

In der Physik wird dagegen die Mechanik in die Kinematik und die Dynamik eingeteilt, die dort die Statik und die Kinetik enthält.

In der Theoretischen Mechanik (auch Analytische Mechanik genannt) geht es dagegen darum, von Axiomen wie den Newtonschen Gesetzen ausgehend eine widerspruchsfreie mathematische Theorie zu entwickeln. In der Technischen Mechanik wird dagegen ein methodischer Aufbau gewählt, der die benötigten Kenntnisse für die Berechnung von Maschinen oder Bauwerken vermittelt.

Teilgebiete der Technischen Mechanik

Die Einteilung der Technischen Mechanik ist nicht überall einheitlich. Im Allgemeinen gelten als Teilgebiete der Technischen Mechanik die folgenden Gebiete.

Statik

Die Statik ist die Mechanik der ruhenden Festkörper. Sie beinhaltet die Statik starrer Körper, die sich nicht verformen, wenn Kräfte auf sie wirken. Alle auf einen ruhenden Körper wirkenden Kräfte sind im Gleichgewicht. Mit dieser Bedingung können aus einer Reihe bekannter Kräfte Gleichungen für unbekannte Kräfte aufgestellt werden. Bei einer Brücke beispielsweise sind die Gewichtskräfte zufolge Eigengewicht bis auf Bautoleranzen bekannt, andere Lasten werden angenommen oder berechnet, die Kräfte in den Lagern (Brückenpfeiler) können damit berechnet werden. In der statischen Berechnung geht es vor allem darum, die Kräfte zu berechnen, die in den zu bemessenden Bauteilen auftreten; im Falle einer Brücke beispielsweise in der Fahrbahnplatte. Der wichtigste Körper in der Statik ist der Balken, dessen Länge sehr viel größer ist als seine Breite und Höhe. Deformierbare Körper sind mit Hilfe der Baustatik berechenbar. Sowohl in der Festigkeitslehre als auch in der Dynamik werden die mit der Statik ermittelten Kräfte als bekannt vorausgesetzt; diese Gebiete bauen also auf der Statik auf.

Festigkeitslehre

Die Festigkeitslehre behandelt prinzipiell deformierbare Körper, also Körper, die sich verformen, aber wie in der Statik in Ruhe sind. In der Elastostatik wird ein Körper als elastisch angenommen, was eine häufige Annahme der Festigkeitslehre ist. Die Festigkeitslehre beinhaltet jedoch auch plastisches und viskoses Materialverhalten wie z.B. beim Kriechen. Die Festigkeitslehre beschäftigt sich auch mit Festigkeits- und Steifigkeitsgesetzen, um Materialeigenschaften beschreiben zu können und steht damit in engem Zusammenhang mit der Werkstofftechnik, die sich hingegen mit Materialien und deren materialspezifischen Eigenschaften selbst beschäftigt. Von großer Bedeutung ist der Begriff der mechanischen Spannung (Kraft pro Querschnittsfläche) und der Dehnung (Längenveränderung relativ zur Gesamtlänge). Unter Annahme des Hooke’schen Gesetzes sind im eindimensionalen Fall bei konstanter Temperatur die Dehnungen direkt proportional zu den wirkenden mechanischen Spannungen. Ein wichtiges Ziel der Festigkeitslehre ist die Berechnung der nötigen Querschnitte von Bauteilen bei gegebenen Kräften und Werkstoffen. Dabei soll sichergestellt werden, dass die auftretenden Spannungen und Verformungen kleiner sind als die zulässigen.

Dynamik

Die Dynamik befasst sich mit Bewegungen und zeitlich veränderlichen Belastungen, die zu Beschleunigungen und somit ebenfalls zu Bewegungen führen. Als Sonderfall der Bewegung gilt grundsätzlich auch der Zustand der Ruhe; da dieser jedoch schon ausführlich in der Statik behandelt wird, werden in diesem Gebiet der Technischen Mechanik Bewegungsvorgänge analysiert mit Geschwindigkeiten ungleich null. Eine wichtige Bewegungsform sind Schwingungen in der Baudynamik und in der Schwingungslehre. In der Technischen Mechanik wird die Dynamik meist eingeteilt in

die Kinematik, die keine Kräfte berücksichtigt, sondern nur die geometrischen Kurven der bewegten Körper beschreibt,
die Kinetik, die auch Kräfte berücksichtigt.

In der Physik, aber teilweise auch in der Technischen Mechanik, versteht man unter Dynamik (griechisch für Kraft) den Teil der Physik, der sich mit Kräften befasst, und teilt sie ein in die Statik (Beschleunigung gleich null) und die Kinetik (Beschleunigung ungleich null).

In der Dynamik geht es in der Regel um feste Körper, sie beinhaltet auch die Fluiddynamik und Aerodynamik. Diese Gebiete sind unter anderem auch in der Baudynamik enthalten, wo z.B. mit Wasserbecken eine Schwingungsdämpfung für Hochhäuser realisiert wird oder bei der Windanregung von Sendemasten.

Spezielle Gebiete

Diese werden teilweise auch als „Höhere Technische Mechanik“ bezeichnet.

Stabilitätstheorie: Die Untersuchung von dynamischer Bewegungsstabilität oder der Stabilität von belasteten Körpern gegen Bruch nach der Theorie II. Ordnung (wie etwa Knickungsvorgänge).
Rotordynamik und Maschinendynamik: Untersuchungen zur Wechselwirkung zwischen dynamischen Kräften und Bewegungsgrößen innerhalb von Maschinen, in denen es gilt, rotierende Baugruppen einer technisch beherrschbaren Rotationsbewegung zu unterwerfen.
Bodenmechanik: Beschreibt Verformungen und Spannungen in Kontinua (z.B. Halbräumen) mit Stoffgesetzen, die den realen Stoffgesetzen von Böden nahekommen.
Biomechanik: Die mechanische Untersuchung lebender Strukturen.
Viskoelastizitätstheorie: Ein Sondergebiet der Kontinuumsmechanik, das sich mit der Untersuchung viskoelastischer Medien befasst.
Kontaktmechanik: Untersuchungen zur statischen und dynamischen (wälzenden oder abrollenden) Berührung von Körpern, insbesondere Erstellung von Modellen zur Flächenpressung in der Berührzone.
Schwingungslehre: Wird auch als Teil der allgemeinen Dynamik verstanden.
Strömungsmechanik
Elastizitätstheorie
Strukturmechanik
Kontinuumsmechanik
Experimentelle Mechanik
Rissmechanik
Finite Elemente Methode
tw. Hydromechanik: Z. B. Staumauern und Wasserversorgung, Schiffe, Wasserturbinen oder Pumpen.
tw. Aerodynamik: Z. B. aerodynamische Effekte bei Hochhäusern, Flugzeugen oder Windrädern.

Im Wesentlichen kann man den Bereich der Technischen Mechanik auf die Ermittlung der Spannungen, Verformungen, Festigkeiten und Steifigkeiten fester Körper sowie der Bewegungen von Festkörpern eingrenzen. Die Ruhelage, ein wichtiger Grenzfall einer Bewegung, wird in der Technischen Mechanik mit Hilfe der Statik bestimmt. Neben der klassischen Technischen Mechanik, die eine geschlossene mathematische Beschreibung in Differentialgleichungen anstrebt, gewinnt die Erarbeitung numerischer Methoden zunehmende Bedeutung. Thermodynamik (z.B.: Wärmetransport oder Kreisprozesse in Motoren und Turbinen) und Strömungslehre (Hydraulik, Fluidmechanik) gelten gewöhnlich nicht als Bestandteile der Technischen Mechanik, sondern als eigenständige Teilgebiete der Ingenieurwissenschaften.

Weitere spezielle Teilgebiete der Technischen Mechanik sind die Lageberechnungen und -regelung der Satelliten und die Ballistik.

Geschichte der Technischen Mechanik

Den meisten Menschen ist es aus der eigenen Intuition heraus gegeben, elementare Probleme der Statik und der Dynamik zu lösen, ohne sich des eigentlichen Hintergrundes bewusst zu sein. Als ein ganz typisches Beispiel für diese Annahme gilt in der Statik der Träger, über dessen Belastbarkeit man schon aus der bloßen Anschauung heraus recht genaue Angaben machen kann.

Formal wurde die Technische Mechanik bereits von Archimedes betrieben, jedoch sind analytisch verwertbare Erkenntnisse erst aus der Zeit der ersten Hälfte des 17. Jahrhunderts überliefert. Die damaligen Mathematiker wurden von den anschaulichen Gesetzen der Mechanik zu ihren neuen Erkenntnissen inspiriert, gleichzeitig entdeckten sie eine Reihe neuer Erkenntnisse und mathematischer Gesetzmäßigkeiten der Technischen Mechanik. In den folgenden Jahrhunderten wurden ihre Theorien in die Technik eingeführt und praktisch umsetzbar gemacht, während weitere theoretische Erkenntnisse folgten. Zeitgleich berechneten die Praktiker den ballistischen Flug einer Kanonenkugel und suchten andererseits die Wirkung dieser Kanonenkugel auf die Mauern einer Festung durch eine geschickte Wahl der äußeren Abmessungen der Festung zu minimieren.

Illustration eines durch eine äußere Last belasteten Balkens in Galileis Discorsi

Der Grieche Archimedes war der erste Mathematiker, der sich eingehend mit mechanischen Problemen befasste. Er entdeckte die Gesetze der Hydrostatik, so wie sie heute noch Gültigkeit besitzen. Simon Stevin entwarf das Kräfteparallelogramm durch das nach ihm benannte Stevinsche Gedankenexperiment. Johannes Kepler beschrieb die Bewegungen der Planeten und Monde mit mathematischen Hilfsmitteln. Die dabei entdeckten Keplerschen Gesetze werden auch heute noch zur Bahnberechnung künstlicher Satelliten und Raumsonden verwendet.

Galileo Galilei kommt in der beginnenden Neuzeit das Verdienst zu, die gerade entstehende Wissenschaft der Technischen Mechanik auf eine formale mathematische Grundlage gestellt zu haben. Der zweite Tag seiner Discorsi befasst sich im Wesentlichen mit der Diskussion von Festigkeitsproblemen. Im gleichen Sinne wirkte Isaac Newton, der mit der Erfindung der Infinitesimalrechnung, basierend auf mechanischen Beobachtungen, Wissenschaftsgeschichte schrieb. Christiaan Huygens lieferte schon praktische Ergebnisse seiner Forschungen in Form der Pendeluhr und genaueren Erkenntnissen der Astronomie. Die Mitglieder der Familie Bernoulli bereiteten im 18. Jahrhundert neben weiteren theoretischen Erkenntnissen den Boden für eine noch heute gültige Technische Mechanik, welche die Grundlage für viele Disziplinen der Technik bildet. Leonhard Euler benannte die Theorien zur Knickung, zur Balkenbiegung und zum Verständnis der modernen Turbinen. Im gleichen Zeitraum begründete Charles Augustin de Coulomb die Grundlagen der Reibungslehre, die ein verbessertes Verständnis für das Funktionieren der gleichzeitig erfundenen Maschinen lieferte. Eine ebenfalls mehr auf die Belange der Praxis abgestimmte Technische Mechanik entwickelten im 19. Jahrhundert Karl Culmann, August Ritter, Giuseppe Cremona und Carlo Alberto Castigliano. Ihre Lösungen mechanischer Probleme basierten mangels leistungsfähiger Rechenmaschinen im Wesentlichen auf exakten geometrischen Zeichnungen. Ein weiterer, bedeutender Name aus der Zeit Ende des 19. und Anfang des 20. Jahrhunderts im Bereich der Technischen Mechanik ist Christian Otto Mohr, von dem die Untersuchungen zum Mohrschen Kreis stammen und der zur selben Zeit an der Technischen Universität Dresden lehrte wie Ludwig Burmester, der Erfinder der gleichnamigen Schablonen.

Im 20. Jahrhundert entstand für die Bedürfnisse der Luft- und Raumfahrt die Aerodynamik durch Nikolai Jegorowitsch Schukowski, Ludwig Prandtl und Theodore von Kármán. Gleichzeitig entwickelten John Argyris und andere Mathematiker die Finite-Elemente-Methode. Der in den dreißiger Jahren sich zur Blüte entwickelnde Hochbau verwendete iterative Verfahren für die statische Berechnung, wie sie von Gaspar Kani oder Hardy Cross veröffentlicht wurden. Alle diese Verfahren nutzen die Numerik als wesentlichen Ansatz.

Viele der genannten Personen haben auch auf anderen Gebieten große Verdienste erworben (z.B. in der Hydromechanik, Optik, Elektrotechnik, Relativitätstheorie und Quantenmechanik). Andererseits war die Technische Mechanik Namensgeberin für eine ganze Klasse mathematischer Objekte: Die Tensoren wurden nach dem Spannungstensor benannt, der im Zusammenhang mit der Elastizitätstheorie eingeführt wurde.

Basierend auf einem Artikel in:

Wikipedia.de