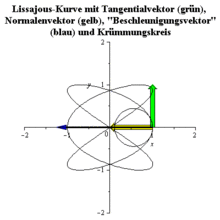
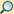Krümmungskreis

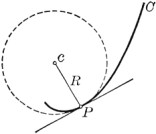
Kurve C (mit örtlich variabler Krümmung) und ihr Krümmungskreis zu Punkt P

Kurve C (mit örtlich gleichbleibender Krümmung) und ihr Krümmungskreis im Extremum P

Der Krümmungskreis (auch Schmiegekreis oder Schmiegkreis genannt) zu einem bestimmten Punkt einer ebenen Kurve ist der Kreis, der die Kurve in diesem Punkt am besten annähert. Den Mittelpunkt des Krümmungskreises nennt man Krümmungsmittelpunkt.

Sein Radius, der Krümmungsradius, ist der Betrag des Kehrwerts der Krümmung der Kurve in . Seine Tangente in diesem Punkt stimmt mit der Tangente der Kurve überein.

Da die Krümmung einer Kurve im Allgemeinen örtlich variiert, schmiegt sich der Krümmungskreis meist nur in einer infinitesimal kleinen Umgebung der vorgegebenen Kurve an. Er verläuft auf der einen Seite des Berührungspunktes innerhalb und auf der anderen Seite außerhalb der Kurve , er schneidet also die Kurve in einem gewissen Abstand von . Nur wenn die Krümmung der Kurve bei dem vorgegebenen Punkt ein Extremum hat, schmiegt sich der Kreis auf einer längeren Strecke der Kurve an die Kurve an und wechselt nicht die Kurvenseite; es gibt dann also keinen Schnittpunkt zwischen Kurve und Krümmungskreis.

Bestimmung

Der Mittelpunkt des Krümmungskreises ist die Grenzlage des Schnittpunktes der Normalen der Kurve, wenn die Kurvenpunkte der Normalen aufeinander zustreben:

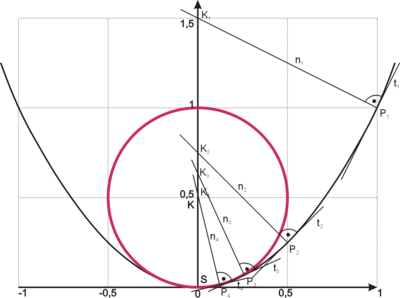
t₁, t₂,... sind die Tangenten, n₁, n₂,... sind die Normalen in den Punkten P₁, P₂,... Die Punkte P₁, P₂,... nähern sich dem Scheitelpunkt S. Die Schnittpunkte K₁, K₂,... nähern sich dem Krümmungsmittelpunkt K

Ist die Kurve in der Parameterdarstellung ${\vec x}(t)\,=\,{\begin{pmatrix}x_{1}(t)\\x_{2}(t)\end{pmatrix}}\,$ gegeben, so ist sein Radius, der Krümmungsradius, gegeben durch

(1) $\displaystyle r=\left|{\frac {{\Big (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\Big )}^{{{\frac {3}{2}}}}}{x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}}\right|$ .

Der Mittelpunkt $K=(K_{x}|K_{y})$ des Krümmungskreises hat dann die Koordinaten

${\vec {x}}(t)\,+\,r\cdot \|{\vec {x}}'(t)\|^{-1}{\begin{pmatrix}-x_{2}'(t)\\x_{1}'(t)\end{pmatrix}}\,$

Dabei muss der Betrag des Radius zur Bestimmung des Mittelpunktes weggelassen werden, damit der Krümmungskreis auf der richtigen Seite der Kurve liegt! Also

(2) $\displaystyle K_{x}=x_{1}(t)-{\frac {x_{2}'(t)\cdot {\Big (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\Big )}}{x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}}$ und

(3) $\displaystyle K_{y}=x_{2}(t)+{\frac {x_{1}'(t)\cdot {\Big (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\Big )}}{x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}}$ .

Der Weg, den die Krümmungskreismittelpunkte beschreiben, bezeichnet man als Evolute der Kurve.

Krümmungsradius eines Funktionsgraphen

Auch für den Graphen einer Funktion lässt sich ein Krümmungsradius angeben. Unter der Krümmung der Funktion an der Stelle $x_{1}=x_{P}$ versteht man die Krümmung des Graphen der Funktion im Punkte ${\Big (}x_{P}|f(x_{P}){\Big )}$ . Mit der Transformation $x_{1}\rightarrow t$ und $f(x_{1})\rightarrow f(t)$ wird die Funktion in eine Parameterdarstellung überführt und es ist:

${\vec x}(t)\,=\,{\begin{pmatrix}t\\f(t)\end{pmatrix}}\,$ .

Die Ableitungen lauten:

${\vec x}'(t)={\begin{pmatrix}1\\f'(t)\end{pmatrix}}$ und $\displaystyle {\vec x}''(t)={\begin{pmatrix}0\\f''(t)\end{pmatrix}}$ .

Damit gilt für den Krümmungsradius $r(x_{P})$ eines Funktionsgraphen an der Stelle $x_{P}$ nach Einsetzen in (1):

(4) $\displaystyle r(x_{P})=\left|{\frac {{\big (}1+f'(x_{P})^{2}{\big )}^{\frac {3}{2}}}{f''(x_{P})}}\right|$ .

Für den Mittelpunkt $(K_{x},K_{y})$ des Krümmungskreises ergibt sich:

(5) $\displaystyle K_{x}=x_{P}-{\frac {f'(x_{P})\,(1+f'(x_{P})^{2})}{f''(x_{P})}}$

(6) $\displaystyle K_{y}=y_{P}+{\frac {1+f'(x_{P})^{2}}{f''(x_{P})}}$

Beispiele

Kreis

Animation der Krümmung bei einem Kreis vom Radius 2, im Uhrzeigersinn durchlaufen

Die Parameterdarstellung eines Kreises lautet:

${\vec x}(t)\,=\,{\begin{pmatrix}\cos(t)\\\sin(t)\end{pmatrix}}$

Die Ableitungen betragen:

${\frac {{\mathrm d}}{{\mathrm d}t}}\cos(t)=-\sin(t)$ ; ${\frac {{\mathrm d}^{2}}{{\mathrm d}t^{2}}}\cos(t)=-\cos(t)$

${\frac {{\mathrm d}}{{\mathrm d}t}}\sin(t)=\cos(t)$ ; ${\frac {{\mathrm d}^{2}}{{\mathrm d}t^{2}}}\sin(t)=-\sin(t)$

Eingesetzt in (1) folgt für den Krümmungsradius eines Einheits-Kreises mit dem Radius von Eins:

Der Krümmungsradius eines Kreises ist konstant und ist so groß wie sein Radius, r=1.

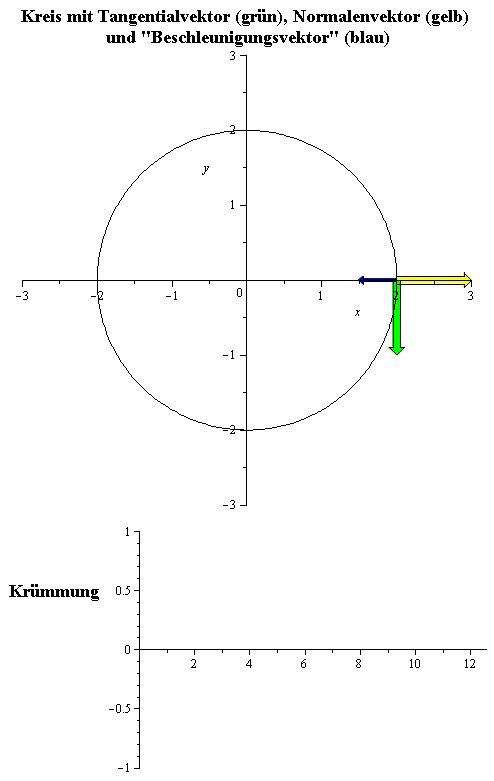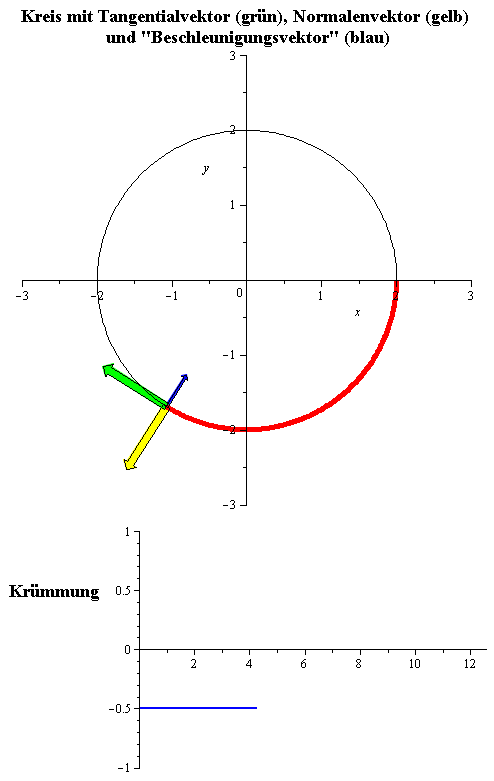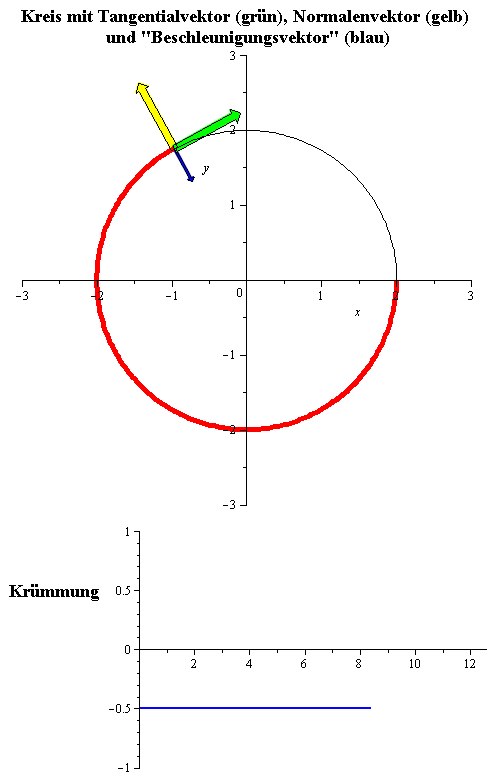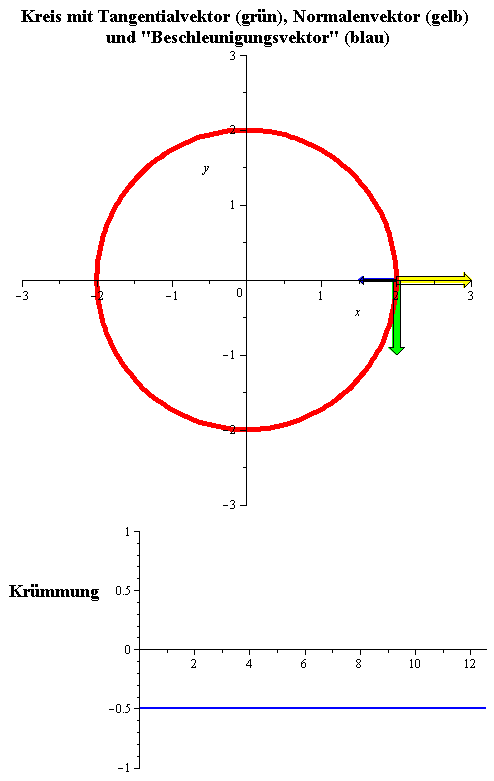
Die nebenstehende Animation zeigt den Kreis vom Radius 2, mit konstanter Geschwindigkeit 1 im Uhrzeigersinn durchlaufen. Er hat Parameterdarstellung

${\vec x}(t)\,=\,{\begin{pmatrix}2\cdot \cos(t/2)\\2\cdot \sin(-t/2)\end{pmatrix}}$

und konstante Krümmung gleich ${\tfrac {1}{2}}$ . Sein Krümmungsradius ist konstant gleich 2, das heißt gleich seinem Radius. (Der "Beschleunigungsvektor" in dieser Animation ist die zweite Ableitung ${\tfrac {{\mathrm {d}}^{2}{\vec {x}}}{{\mathrm {d}}t^{2}}}$ .)

Parabel

Der Krümmungskreis einer Normalparabel in ihrem Scheitelpunkt hat den Radius 0,5

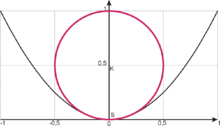
Für die Normalparabel $f(x)=x^{2}$ gilt:

$f'(x)=2\cdot x$

Setzt man in (4) ein, folgt für den Krümmungsradius:

$r(x)=\left|{\frac {\left(1+4\cdot x^{2}\right)^{{{\frac {3}{2}}}}}{2}}\right|$

An der Stelle x=0 beträgt der Krümmungsradius r=0,5 (siehe Abbildung). Für große x wächst der Krümmungsradius ~ x³, die Kurve wird immer gerader.

Lissajous-Kurve

Animation des Krümmungs- kreises bei einer Lissajous-Kurve

Die Parameterdarstellung einer Lissajous-Kurve mit Frequenzverhältnis 2:3 lautet

${\vec x}(t)\,=\,{\begin{pmatrix}\cos(3t)\\\sin(2t)\end{pmatrix}}$

Die ersten Ableitungen betragen:

${\frac {{\mathrm d}{\vec x}(t)}{{\mathrm d}t}}\,=\,{\begin{pmatrix}-3\sin(3t)\\2\cos(2t)\end{pmatrix}}\,$ /DD>

Die zweiten Ableitungen betragen:

${\frac {{\mathrm d}^{2}{\vec x}(t)}{{\mathrm d}t^{2}}}\,=\,{\begin{pmatrix}-9\cos(3t)\\-4\sin(2t)\end{pmatrix}}\,$

Setzt man dies in (1) ein und benutzt die Additionstheoreme für Sinus und Kosinus, so folgt für den Krümmungsradius dieser Lissajous-Kurve:

$r(t)\,=\,{\frac {(232\cos(t)^{4}-97\cos(t)^{2}+13-144\cos(t)^{6})^{{3/2}}}{6\cos(t)(8\cos(t)^{4}-10\cos(t)^{2}+5)}}\,\,.$

Die Abbildung zeigt eine Animation des Krümmungskreises. Der „Beschleunigungsvektor“ in dieser Abbildung ist die zweite Ableitung ${\tfrac {{\mathrm {d}}^{2}{\vec {x}}}{{\mathrm {d}}s^{2}}}$ von ${\vec {x}}$ nach der Bogenlänge .

Siehe auch

Klothoide, Krümmungsradius ist umgekehrt proportional zur Kurvenlänge
Schmiegkugel, eine Verallgemeinerung auf Raumkurven

Literatur

Christian Blatter: Analysis 2. Springer, 1974, S. 90–93

Basierend auf einem Artikel in:

Wikipedia.de