Schmiegkugel
Die Schmiegkugel, oder Schmiegekugel oder in älterer Literatur Schmiegungskugel, ist im mathematischen Teilgebiet der Differentialgeometrie eine Kugel, die sich einer regulären Kurve im dreidimensionalen Anschauungsraum in einem gegebenen Kurvenpunkt bestmöglich anschmiegt. Es handelt sich um die Verallgemeinerung des Krümmungskreises oder Schmiegkreises einer ebenen Kurve auf Raumkurven.
Definitionen
Es sei
eine Frenet-Kurve
und
sei ein Punkt aus dem Inneren
des Definitionsintervalls
.
Man sagt, eine Kugel mit Mittelpunkt
und Radius
schmiege sich der Kurve an der Stelle
bzw. in
optimal an, wenn möglichst viele Ableitungen
der Funktion
in
verschwinden. Verschwinden die ersten
Ableitungen, was entsprechende Differenzierbarkeitsvoraussetzungen
an
erfordert, so sagt man, die Kugel berühre
im Punkt
in
-ter
Ordnung.
Es sei weiter
das begleitende
Frenet-Dreibein und
und
seien Krümmung beziehungsweise
Torsion
der Kurve
.
Eindeutige Existenz der Schmiegkugel
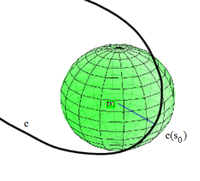
Die Frenet-Kurve
habe im Punkt
eine von 0 verschiedene Krümmung und Torsion.
Dann gibt es genau eine Kugel, die die Kurve im Punkt
in dritter Ordnung berührt und mit obigen Bezeichnungen gelten für Mittelpunkt
und Radius folgende Formeln:
Da
und da das Frenet-Dreibein ein Orthonormalsystem
ist, ergibt sich die Radiusformel direkt aus der Mittelpunktsformel.
Man beachte, dass
in dieser Formel nicht vorkommt, das heißt der Mittelpunkt der Schmiegkugel
liegt stets in der Normalebene, das ist die zum Tangentenvektor
orthogonale Ebene durch den Kurvenpunkt
.
Sphärische Kurven
Frenet-Kurven mit nicht-verschwindender Torsion, deren Bild in einer festen Kugeloberfläche liegt, zeichnen sich dadurch aus, dass ihre Schmiegkugeln in jedem Punkt mit dieser festen Kugel übereinstimmen, solche Kurven nennt man sphärisch. Insbesondere ist der Mittelpunkt
konstant. Es muss also
gelten. Wertet man diese Bedingung unter Hinzuziehung der frenetschen Formeln
aus, so erhält man:
Das Bild einer viermal differenzierbaren Frenet-Kurve mit
nicht-verschwindender Torsion liegt genau dann in einer festen Kugeloberfläche,
wenn Krümmung
und Torsion
der folgenden Differentialgleichung
genügen:
.
Für Kurven mit verschwindender Torsion kann eine solche Charakterisierung natürlich nicht gelten, Beispiele für solche Kurven sind in einer Kugeloberfläche enthaltene Kreise, denn diese haben als ebene Kurven die Torsion 0.
Schon wegen des Hauptsatzes der Kurventheorie können Krümmung und Torsion für sphärische Kurven nicht unabhängig sein. Da es sich um differentielle Größen handelt, muss man eine Beziehung in Form einer Differentialgleichung zwischen ihnen erwarten. Man beachte, dass die oben angegebene Differentialgleichung eine Überprüfung der sphärischen Eigenschaft erlaubt, ohne die Kugel dazu ermitteln zu müssen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.07. 2021