Kurve (Mathematik)
In der Mathematik ist eine Kurve (von lateinisch curvus „gebogen, gekrümmt“) ein eindimensionales Objekt. Im Gegensatz etwa zu einer Geraden muss eine Kurve grundsätzlich keinen geraden, sondern kann vielmehr jeden beliebigen Verlauf annehmen.
Eindimensional bedeutet dabei informell, dass man sich auf der Kurve nur in eine Richtung (bzw. in die Gegenrichtung) bewegen kann. Ob die Kurve in der zweidimensionalen Ebene liegt („ebene Kurve“) oder in einem höherdimensionalen Raum (siehe Raumkurve), ist in diesem begrifflichen Zusammenhang unerheblich.
Je nach Teilgebiet der Mathematik gibt es unterschiedliche Präzisierungen dieser Beschreibung.
Parameterdarstellungen
Eine Kurve kann als das Bild
eines Weges
definiert werden. Ein Weg ist (abweichend von der Umgangssprache) eine stetige
Abbildung von einem Intervall
in den betrachteten Raum, also z.B. in die euklidische Ebene .
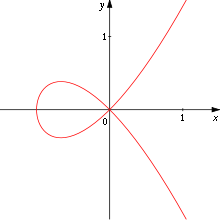
Beispiele:
- Die Abbildung
-
- beschreibt den Einheitskreis in der Ebene.
- Die Abbildung
-
- beschreibt eine Kurve mit einem einfachen Doppelpunkt bei
, entsprechend den Parameterwerten
und
.
Gelegentlich, insbesondere bei historischen Bezeichnungen, wird zwischen Weg und Kurve nicht unterschieden. So ist die interessante Struktur bei der Hilbert-Kurve der Weg; das Bild dieses Weges ist das Einheitsquadrat, besitzt also keinerlei fraktale Struktur mehr.
Durch die Parameterdarstellung erhält die Kurve einen Richtungssinn in der Richtung des wachsenden Parameters.>
Gleichungsdarstellungen
Eine Kurve kann auch durch eine oder mehrere Gleichungen in den Koordinaten beschrieben werden. Beispiele dafür sind wieder die Bilder der beiden durch die obigen Parameterdarstellungen gegebenen Kurven:
- Die Gleichung
-
- beschreibt den Einheitskreis in der Ebene.
- Die Gleichung
-
- beschreibt die oben in Parameterdarstellung angegebene Kurve mit Doppelpunkt.
Ist die Gleichung wie hier durch ein Polynom gegeben, nennt man die Kurve algebraisch.
Funktionsgraphen
Funktionsgraphen sind ein Spezialfall beider oben angegebenen Formen: Der Graph einer Funktion
kann entweder als Parameterdarstellung
oder als Gleichung
angegeben werden.
Wird in der Schulmathematik von Kurvendiskussion gesprochen, so meint man üblicherweise nur diesen Spezialfall.
Differenzierbare Kurven, Krümmung
Sei
ein Intervall und
eine reguläre Kurve, d.h.
für alle
.
Die Länge
der Kurve ist
Die Funktion
ist ein Diffeomorphismus
,
und die Verkettung von
mit dem inversen Diffeomorphismus liefert eine neue Kurve
mit
für alle
.
Man sagt:
ist nach der Bogenlänge parametrisiert.
Sei
ein Intervall und
eine nach der Bogenlänge parametrisierte Kurve. Die Krümmung
von
an der Stelle
ist definiert als
.
Für ebene Kurven kann man die Krümmung noch mit einem Vorzeichen versehen:
Ist
die Drehung um 90°, dann ist
festgelegt durch
.
Positive Krümmung entspricht Linkskurven, negative Rechtskurven.
Geschlossene Kurven
Sei
eine ebene Kurve. Sie heißt geschlossen, wenn
,
und einfach geschlossen, wenn zusätzlich
auf
injektiv ist. Der Jordansche
Kurvensatz besagt, dass eine einfach geschlossene Kurve die Ebene in einen
beschränkten
und einen unbeschränkten Teil zerlegt. Ist
eine geschlossene Kurve mit
für alle
,
kann man der Kurve eine Umlaufzahl
zuordnen, die angibt, wie oft die Kurve um den Nullpunkt herumläuft.
Glatten geschlossenen Kurven kann man eine weitere Zahl zuordnen, die Tangentenumlaufzahl,
die für eine nach der Bogenläge parametrisierte Kurve
durch
gegeben ist. Der Umlaufsatz
von Heinz
Hopf besagt, dass eine einfache geschlossene Kurve Tangentenumlaufzahl
oder
hat.
Sei allgemein
ein topologischer
Raum. Statt von geschlossenen Wegen
mit
spricht man auch von Schleifen mit Basispunkt
.
Weil der Quotientenraum
homöomorph
zum Einheitskreis
ist, identifiziert man Schleifen mit stetigen Abbildungen
.
Zwei Schleifen
mit Basispunkt
heißen homotop, wenn man sie unter
Beibehaltung des Basispunkts stetig ineinander deformieren kann, d.h. wenn
es eine stetige Abbildung
mit
,
für alle
und
für alle
gilt. Die Äquivalenzklassen homotoper Schleifen bilden eine Gruppe, die Fundamentalgruppe von
.
Ist
,
dann ist die Fundamentalgruppe über die Windungszahl isomorph zu
.
Raumkurven
Sei
ein Intervall und
eine nach der Bogenlänge parametrisierte Kurve. Die folgenden Bezeichnungen sind
Standard:
(definiert, wann immer ).
ist der Tangentialvektor,
der Normalenvektor und
der Binormalenvektor, das Tripel
heißt begleitendes
Dreibein. Die Krümmung ist
,
die Windung
definiert durch
.
Es gelten die frenetschen
Formeln:
Der Hauptsatz
der lokalen Kurventheorie besagt, dass man eine Kurve aus Krümmung und
Windung rekonstruieren kann: Sind glatte Funktionen
mit
für alle
(der Wert 0 ist für
also nicht erlaubt), so gibt es bis auf Bewegungen
genau eine entsprechende Kurve.
Die von je zwei der drei Vektoren ,
oder
aufgespannten Ebenen durch den Kurvenpunkt tragen besondere Namen:
- Die Oskulationsebene
oder Schmiegebene wird von
und
aufgespannt.
- Die Normalebene wird von
und
aufgespannt.
- Die rektifizierende Ebene oder Streckebene wird von
und
aufgespannt.
Kurven als eigenständige Objekte
Kurven ohne umgebenden Raum sind in der Differentialgeometrie
relativ uninteressant, weil jede eindimensionale Mannigfaltigkeit diffeomorph
zur reellen Geraden
oder zur Einheitskreislinie
ist. Auch Eigenschaften wie die Krümmung
einer Kurve sind intrinsisch nicht feststellbar.
In der algebraischen Geometrie und damit zusammenhängend in der komplexen Analysis versteht man unter „Kurven“ in der Regel eindimensionale komplexe Mannigfaltigkeiten, oft auch als Riemannsche Flächen bezeichnet. Diese Kurven sind eigenständige Studienobjekte, das prominenteste Beispiel sind die elliptischen Kurven. Siehe Kurve (algebraische Geometrie)
Historisches
Das erste Buch der Elemente von Euklid begann mit der Definition „Ein Punkt ist, was keine Teile hat. Eine Kurve ist eine Länge ohne Breite.“
Diese Definition lässt sich heute nicht mehr aufrechterhalten, denn es gibt
zum Beispiel Peano-Kurven,
d.h. stetige surjektive
Abbildungen ,
die die gesamte Ebene ausfüllen. Andererseits folgt aus dem Lemma
von Sard, dass jede differenzierbare Kurve den Flächeninhalt null, also
tatsächlich wie von Euklid gefordert „keine Breite“ hat.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.06. 2021