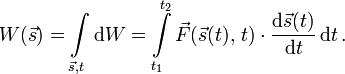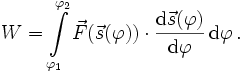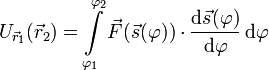Raumkurve
Eine Raumkurve ist eine Kurve im dreidimensionalen Raum.
Ihre theoretische Untersuchung ist ein Gegenstand der Differentialgeometrie. Angewandt spielen Raumkurven unter anderem in der klassischen Mechanik als Bahnkurven und in der Strömungslehre als charakteristische Linien eine wichtige Rolle.
In der (klassischen) Mechanik lässt sich die Bahn eines Massenpunktes im Raum mathematisch als Raumkurve beschreiben. Hier ist eigentlich die Bezeichnung Weg zutreffender, da Bahnkurven durch die Zeit parametrisiert sind. Weitere Anwendungen sind die charakteristischen Linien in Strömungen, wie z.B. Stromlinien und Bahnlinien. Die beiden Begriffe fallen für stationäre Strömungen zusammen. Dieser Artikel widmet sich vorwiegend der Anwendung in der klassischen Mechanik. Dabei werden die betrachteten mathematischen Funktionen stets als hinreichend oft differenzierbar vorausgesetzt.
Anwendungen in der Mechanik
Bahnkurven
Mathematisch lassen sich Raumkurven mit den Frenetschen Formeln
beschreiben. Dabei wird jedem Punkt der Kurve ein begleitendes Dreibein
aus Tangenteneinheitsvektor 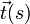 ,
Hauptnormaleneinheitsvektor
,
Hauptnormaleneinheitsvektor 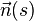 und Binormaleneinheitsvektor
und Binormaleneinheitsvektor 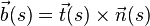 zugeordnet. Die genaue Definition und geometrische Bedeutung dieser Vektoren
wird im Artikel Frenetsche
Formeln erläutert.
zugeordnet. Die genaue Definition und geometrische Bedeutung dieser Vektoren
wird im Artikel Frenetsche
Formeln erläutert.
Beschreibt die Raumkurve den Ort eines Massenpunktes zum Zeitpunkt t, dann haben die dadurch gegebenen Richtungen folgende physikalische Bedeutung:
| Richtung des Dreibeinvektors | Richtung der vektoriellen Größe | ||
| Tangenteneinheitsvektor | 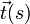 |
Momentangeschwindigkeit | 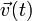 |
| Hauptnormaleneinheitsvektor | 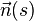 |
Zentralanteil der Momentanbeschleunigung | 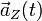 |
| Binormaleneinheitsvektor | 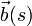 |
Momentaner Drehimpuls bezogen auf den Krümmungsmittelpunkt | 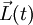 |
Arbeit und Potential
Die Definition des Arbeitsintegrals erfolgt über eine (gedachte) Raumkurve:
Dabei bewegt sich ein (gedachter) Massenpunkt zwischen den Zeitpunkten
t1 und t2 auf dem Weg 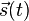 vom Anfangspunkt
vom Anfangspunkt 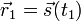 zum Endpunkt
zum Endpunkt 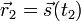 durch das vom Ort
durch das vom Ort 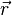 und der Zeit t abhängige Kraftfeld
und der Zeit t abhängige Kraftfeld 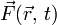 .
Das Differential
dW dieses Integrals ist die physikalische Arbeit, sein Wert
.
Das Differential
dW dieses Integrals ist die physikalische Arbeit, sein Wert 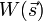 ist die von dem Massenpunkt aufgenommene Energie.
ist die von dem Massenpunkt aufgenommene Energie.
In einem stationären Kraftfeld (das sich zeitlich nicht ändert) sind Arbeit
und Arbeitsintegral zeitunabhängig, die Raumkurve 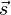 kann dann mit einer beliebigen Variablen
kann dann mit einer beliebigen Variablen 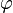 parametrisiert werden und das Arbeitsintegral vereinfacht sich zu
parametrisiert werden und das Arbeitsintegral vereinfacht sich zu
Wenn dieses Arbeitsintegral in einem Raumgebiet V allein vom Anfangs-
und Endpunkt und nicht von der Wahl des Weges 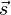 abhängig ist, dann kann es zur Definition eines Potentials
abhängig ist, dann kann es zur Definition eines Potentials
auf V verwendet werden. Die skalare Funktion 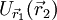 gibt bei festem Anfangspunkt
gibt bei festem Anfangspunkt 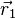 die potentielle
Energie des Ortes
die potentielle
Energie des Ortes 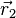 (bezogen auf
(bezogen auf 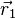 )
an.
)
an.
Beispiele für Bahnkurven
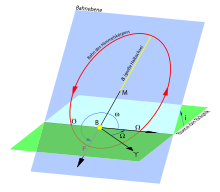
- Die Bahnen von künstlichen Satelliten um die Erde und der Planeten um die Sonne sind, wenn man von kleinen Bahnstörungen absieht, ebene Bahnkurven genauer Kepler-Ellipsen, in deren einem Brennpunkt die Erde bzw. Sonne steht.
- Allgemeiner ist in jedem Zentralfeld die Bahn eines Körpers eine ebene Kurve. Dies ist eine der Aussagen des Drehimpulserhaltungssatzes: Seine Richtung und damit die des Binormalenvektors ist konstant.
- In einem homogenen magnetischen Feld beschreiben geladene Teilchen spiralförmige Bahnen (Schraubenlinien) um die Magnetfeldlinien.
Sonstiges
- Bei Geschwindigkeiten, die gegenüber der Lichtgeschwindigkeit nicht vernachlässigbar klein sind, versagt das mathematische Modell der Raumkurve zur Beschreibung der Bahn eines Massenpunktes. An die Stelle der Raumkurve tritt dann die Weltlinie in der vierdimensionalen Raumzeit.
- Die Differenzierbarkeitsbedingungen, die herkömmlich an die Wege und Felder gestellt werden, können durch eine verallgemeinerte Interpretation des Ableitungsbegriffs (Ableitung im Distributionensinn) stark abgeschwächt werden. Dies ist in den Anwendungen vor allem für die Felder von Bedeutung, die von punktförmigen Zentren ausgehen.


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 24.07. 2021