Rotationsfläche

Rotation eines cos-Bogens (s.u.)

Torus als Rotationsfläche

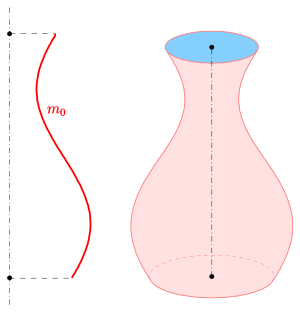
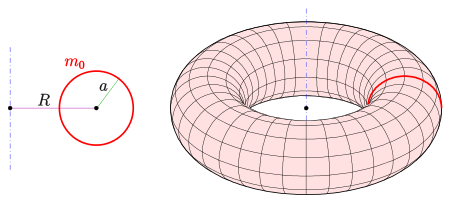
Eine Rotationsfläche oder Drehfläche ist in der Geometrie eine Fläche, die durch Rotation einer ebenen Kurve, des Hauptmeridians, um eine in derselben Ebene liegende Gerade, die Rotationsachse, entsteht. Ein einfaches Beispiel ist ein gerader Kreiskegel. Er entsteht durch Rotation einer Gerade um eine sie schneidende Rotationsachse. Weitere einfache Beispiele sind: gerader Kreiszylinder (Rotation einer Gerade um eine dazu parallele Achse), Kugel (Rotation eines Kreises um einen Durchmesser) und Torus (Rotation eines die Achse nicht schneidenden Kreises). Rotationsflächen haben gegenüber anderen Flächen besondere Eigenschaften:

Rotationsflächen sind rotationssymmetrisch, d. h. die wesentlichen geometrischen Informationen sind schon im Hauptmeridian enthalten. Sie haben deswegen relativ einfache analytische Beschreibungen.
Ein Schnitt mit einer beliebigen Ebene, die die Rotationsachse enthält, heißt Meridian und ist immer kongruent zum Hauptmeridian.
Ein Querschnitt, d.h. ein ebener Schnitt mit einer Ebene senkrecht zur Rotationsachse, ist immer ein Kreis und heißt Breitenkreis.
Die Meridiane und Breitenkreise sind die Krümmumgslinien der Rotationsfläche. (Sie schneiden sich senkrecht und geben in jedem Punkt die Richtungen maximaler und minimaler Normalkrümmungen an (siehe Torus).)

Weitere Beispiele: Rotationsellipsoid, Rotationsparaboloid, Rotationshyperboloid.

Bemerkung:

Eine Rotationsfläche lässt sich auch durch die Rotation einer geeigneten anderen Kurve, die nicht mit der Rotationsachse in einer Ebene liegt, erzeugen. Ein einfaches Beispiel ist das Rotationshyperboloid. Es lässt sich durch Rotation einer auf ihr liegenden (zur Rotationsachse windschiefen) Gerade erzeugen. Die erzeugende Gerade ist kein Meridian.
Der Umriss einer Rotationsfläche ist im Allgemeinen kein Meridian oder ein anderer ebener Schnitt.

Analytische Beschreibungen

Rotation eines Punktes

Die analytische Beschreibung einer Rotationsfläche hängt direkt von der analytischen Beschreibung der rotierten ebenen Kurve, des Hauptmeridians, ab. Im Folgenden wird immer vorausgesetzt, dass die z-Achse die Rotationsachse ist.

Lässt man den Punkt $(r_{0},0,z_{0}),\ r_{0}\geq 0$ der x-z-Ebene um die z-Achse rotieren, so erhält man den Kreis $(r_{0}\cos \varphi ,r_{0}\sin \varphi ,z_{0}),\ 0\leq \varphi <2\pi \ ,$ mit Radius $r_{0}$ .

Meridian in Parameterform

Kegel als Rotationsfläche

Ellipsoid als Rotationsfläche

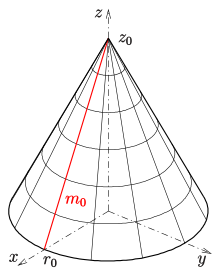
In diesem Fall wird vorausgesetzt, dass

der Hauptmeridian $m_{0}$ die Kurve $(r(t),0,z(t)),\ t_{1}\leq t\leq t_{2}$ mit $r(t)\geq 0$ ist.

Die Parameterform der zugehörigen Rotationsfläche ist dann

$(r(t)\cos \varphi ,r(t)\sin \varphi ,z(t)),\ \ t_{1}\leq t\leq t_{2},0\leq \varphi <2\pi \ .$

Für geometrische Betrachtungen ist es meist wichtig eine Flächennormale zur Verfügung zu haben. Unter entsprechenden Differenzierbarkeitsvoraussetzungen ergibt sich für eine Normale in einem Flächenpunkt $(r\cos \varphi ,r\sin \varphi ,z)\ :$

${\vec {n}}=({\dot {z}}\cos \varphi ,{\dot {z}}\sin \varphi ,-{\dot {r}})\ .$

Für den Oberflächeninhalt ergibt sich (ohne mögliche Boden- und Deckelkreise !)

$A=2\pi \int _{t_{1}}^{t_{2}}r\ {\sqrt {{\dot {r}}^{2}+{\dot {z}}^{2}}}\,dt,$ .

Beispiele:

1) $m_{0}:(r_{0}t,0,z_{0}(1-t)),\ 0\leq t\leq 1$ (Strecke) ergibt den Kegel

$(r_{0}t\cos \varphi ,r_{0}t\sin \varphi ,z_{0}(1-t),\ \ 0\leq t\leq 1,0\leq \varphi <2\pi \ ,$

mit Grundkreisradius $r_{0}$ und der Höhe $z_{0}$ .

2) $m_{0}:(R+a\cos t,0,a\sin t),\ 0\leq t\leq 2\pi ,\ R>a$ (Kreis) ergibt den Torus (s. Bild)

$((R+a\cos t)\cos \varphi ,(R+a\cos t)\sin \varphi ,a\sin t),\ 0\leq t\leq 1,0\leq \varphi <2\pi \ .$

3) $m_{0}:(a\cos t,0,b\sin t),\ 0\leq t\leq \pi ,\$ (Halbellipse) ergibt das Rotationsellipsoid

$(a\cos t\cos \varphi ,a\cos t\sin \varphi ,b\sin t)\ 0\leq t\leq \pi ,\ 0\leq \varphi <2\pi \ .$

4) $m_{0}:(a\cos 2\pi {\tfrac {t-b}{l}}+c,0,t),\ 0\leq t\leq h,\$ (Kosinuskurve) ergibt

$\left((a\cos 2\pi {\tfrac {t-b}{l}}+c)\cos \varphi ,(a\cos 2\pi {\tfrac {t-b}{l}}+c)\sin \varphi ,t\right)\ 0\leq t\leq h,\ 0\leq \varphi <2\pi \ .$

Für das erste Bild (Vase) wurden folgende Parameter verwendet:

Meridian in impliziter Form

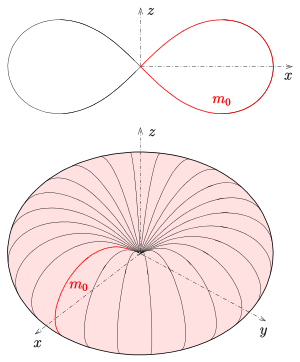
Rotationsfläche, Meridian=Cassini-Kurve

In diesem Fall wird vorausgesetzt, dass

der Hauptmeridian $m_{0}$ die in der r-z-Ebene durch die Gleichung mit $r\geq 0$ implizit gegebene Kurve ist.

Die implizite Darstellung der zugehörigen Rotationsfläche ergibt sich durch die Ersetzung $r={\sqrt {x^{2}+y^{2}}}\ :$

$f({\sqrt {x^{2}+y^{2}}},z)=0\ .$

Eine Flächennormale in einem Flächenpunkt $(x,y,z)=(r\cos \varphi ,r\sin \varphi ,z)$ ist:

${\vec {n}}=(f_{r}\cos \varphi ,f_{r}\sin \varphi ,f_{z})\ .$

Beispiele:

1) $m_{0}:z_{0}r+r_{0}z-r_{0}z_{0}=0,\ r_{0},z_{0}>0,\ 0\leq r\leq r_{0}\ ,$ (Strecke) ergibt den Kegel mit der Gleichung

$z_{0}^{2}(x^{2}+y^{2})=r_{0}^{2}(z_{0}-z)^{2}\ ,$ dem Grundkreisradius $r_{0}$ und der Höhe $z_{0}$ .

2) $m_{0}:(r-R)^{2}+z^{2}-a^{2}=0,R>a>0\ ,$ (Kreis) ergibt den Torus mit der Gleichung

$(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0\ .$

3) $m_{0}:(r^{2}+z^{2})^{2}-2c^{2}(r^{2}-z^{2})-(a^{4}-c^{4})=0,a>0,c>0\ ,$ (Cassini-Kurve) ergibt die Fläche mit der Gleichung

$(x^{2}+y^{2}+z^{2})^{2}-2c^{2}(x^{2}+y^{2}-z^{2})-(a^{4}-c^{4})=0$

Für das Bild wurde a=c=1

(Lemniskate) gewählt.

Guldinsche Regeln

Die erste guldinsche Regel, benannt nach dem Schweizer Mathematiker Paul Guldin, verkürzt die Berechnungen von Rotationsflächen enorm, falls sich die Linien- oder Flächenschwerpunkte der rotierenden Objekte unter Ausnutzen der Symmetrien der jeweiligen Aufgabe einfach erkennen lassen.

Bezeichnungen:

= Flächeninhalt

= Länge der erzeugenden Linie (Profillinie)

= Radius des Schwerpunktkreises

= Radius des rotierenden Kreises (Torus-Beispiele)

Der Flächeninhalt einer Rotationsfläche, dessen Rotationsachse die erzeugende Linie nicht schneidet, ist gleich dem Produkt aus der Länge der erzeugenden Linie (Profillinie) und dem Umfang des Kreises (Schwerpunktkreis), der durch die Rotation des Schwerpunktes der Profillinie erzeugt wird:

$A=L\cdot 2\pi R$

Ausgedrückt in Abhängigkeit von der Funktion der erzeugenden Linie ergibt sich der Flächeninhalt als:

Bei Rotation um die x-Achse

$A=2\pi \int _{a}^{b}f(x){\sqrt {1+\left[f'(x)\right]^{2}}}\mathrm {d} x$

Mit $\textstyle R=y_{s}={\frac {1}{L}}\int _{L}y\mathrm {d} L$ als >-Koordinate des Linienschwerpunktes der Linie und ihrem Linienelement $\mathrm {d} L$ findet man

$A=L\cdot 2\pi R=L\cdot 2\pi \cdot {\frac {1}{L}}\int _{L}f(x)\mathrm {d} L=2\pi \int _{L}f(x)\mathrm {d} L$ ,

was das obige Ergebnis darstellt, wenn noch $\textstyle \mathrm {d} L={\sqrt {(\mathrm {d} x)^{2}+(\mathrm {d} y)^{2}}}={\sqrt {1+\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}}}\mathrm {d} x$ mit den -Intervallgrenzen [a,b] eingesetzt wird.

Bei Rotation um die y-Achse

$A=2\pi \int _{\min(f(a),f(b))}^{\max(f(a),f(b))}f^{-1}(y){\sqrt {1+\left[\left(f^{-1}(y)\right)'\right]^{2}}}\mathrm {d} y$

Wie oben bei der Volumenberechnung muss auch hier gegebenenfalls die Rechnung für die stetigen und streng monotonen Abschnitte von f(x) , in denen die Umkehrfunktion existiert, separat durchführt werden.

Beispiel: Oberfläche eines Rotationstorus:

$A=2\pi r\cdot 2\pi R=4\pi ^{2}rR$

Parameterform

Wenn eine Kurve durch ihre Parameterform $(x(t),y(t))$ in einem Intervall [a,b] definiert wird, sind die Flächeninhalte der Rotationsflächen, die durch Drehen der Kurve um die x-Achse oder die y-Achse erzeugt werden, gegeben durch

$A_{x}=\int _{a}^{b}2\pi y\,{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t$

$A_{y}=\int _{a}^{b}2\pi x\,{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t$

Typen

Rotationsflächen konstanter gaußscher Krümmung wurden von Carl Friedrich Gauß und Ferdinand Minding klassifiziert. Rotationsflächen mit verschwindender gaußscher Krümmung sind die Ebene, der Zylinder und der Kegel. Rotationsflächen mit positiver gaußscher Krümmung sind die Kugeloberfläche, die Flächen vom Spindeltyp und die Flächen vom Wulsttyp. Rotationsflächen mit negativer gaußscher Krümmung sind die Pseudosphäre, die auch als mindingsche Fläche bekannt ist, die Flächen vom Kegeltyp und die Flächen vom Kehltyp. Die Kugeloberfläche und die Pseudosphäre haben konstante Gaußsche Krümmung.

Siehe auch

Literatur

W. Kühnel: Differentialgeometrie, Vieweg-Verlag, Braunschweig/Wiesbaden, 2003, ISBN 3-528-17289-4, S. 52
>Karl Strubecker: Differentialgeometrie (Band III), Sammlung Göschen, Band 1180, De Gruyter, Berlin, 1959

Basierend auf einem Artikel in:

Wikipedia.de