Mantelfläche

Als Mantelfläche oder kurz Mantel bezeichnet man in der Geometrie einen Teil der Oberfläche bestimmter Körper. In diesem Artikel wird die Mantelfläche von Rotationskörpern behandelt, zu denen unter anderem der Zylinder, der Kegel und der Kegelstumpf zählen. Zur Mantelfläche bei Nicht-Rotationskörpern wird auf die jeweiligen Artikel verwiesen (siehe z.B. Pyramide und Prisma). „Boden“ (Grundfläche) und „Deckel“ (Deckfläche) des Körpers werden, falls vorhanden, in der Regel nicht zum „Mantel“ (Mantelfläche) gezählt und gelegentlich als „Stirnflächen“ bezeichnet.

Die Mantelfläche von Zylinder, Kegel und Kegelstumpf kann durch „Abrollen“ oder „Abwickeln“ zweidimensional dargestellt werden. Zur Berechnung der Fläche genügen in diesen Fällen einfache geometrische Formeln. Allgemein gilt für Rotationskörper, dass ihre Mantelfläche durch Rotation eines Graphen einer Funktion um eine Koordinatenachse entsteht. Bei diesem Ansatz wird die Integralrechnung zur Berechnung der Fläche benötigt.

Mantelfläche des Kreiszylinders

Gerader Kreiszylinder mit abgerollter Mantelfläche

Die blaue Fläche im nebenstehenden Bild entspricht der Mantelfläche des gezeigten Kreiszylinders. Dieser könnte etwa durch Rotation einer konstanten Funktion um eine Koordinatenachse entstehen.

Interessant ist, dass die Mantelfläche eines Zylinders, der gerade eine Kugel in sich aufnehmen kann (Zylinderradius = Kugelradius und Zylinderhöhe $h=2r$ ), mit der Oberfläche der Kugel übereinstimmt.

Mantelfläche des Kegels

Siehe dazu Kegel (Geometrie)#Mantelfläche.

Mantelfläche des Kegelstumpfs

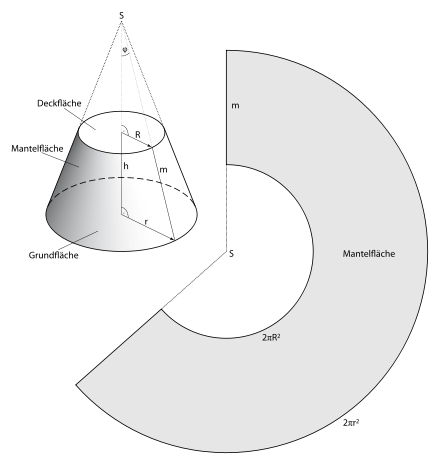
Kegelstumpf und seine abgewickelte Mantelfläche

Die punktierte Fläche im nebenstehenden Bild entspricht der Mantelfläche des gezeigten Kegelstumpfs, betrachtet in der Draufsicht. Dieser könnte etwa durch Rotation einer Geraden um eine Koordinatenachse entstehen.

Herleitung

Es sei $M_{{\mathrm {G}}}\$ die Mantelfläche des ganzen Kegels, $M_{{\mathrm {H}}}\$ die Mantelfläche vom kleinen Kegel und $M_{{\mathrm {KS}}}\$ die Mantelfläche vom Kegelstumpf, dann errechnet sich die Mantelfläche $M_{{\mathrm {KS}}}\$ des Kegelstumpfes durch $M_{{\mathrm {KS}}}=M_{{\mathrm {G}}}-M_{{\mathrm {H}}}\$

Nun bezeichnet man zusätzlich zu den in der Skizze bereits festgelegten Variablen die Verlängerung der Höhe zur Spitze mit und die Verlängerung der Seitenlänge $m\$ zur Spitze des Kegels mit $s_{{\mathrm {x}}}\$ .

Mit Hilfe dieser Notation verifiziere man anschließend

$(1)~~M_{\mathrm {KS} }=M_{\mathrm {G} }-M_{\mathrm {H} }=\pi r(m+s_{\mathrm {x} })-\pi Rs_{\mathrm {x} }$

(Hinweis zu den Formeln für $M_{{\mathrm {G}}}\$ und $M_{{\mathrm {H}}}\$ : Für die Fläche eines Kreissegments gilt $A=\pi r^{2}{\alpha \over 360^{\circ }}\$ und für den Segmentbogen $b=2\pi r{\alpha \over 360^{\circ }}=\pi r{\alpha \over 180^{\circ }}\$ woraus $A={1 \over 2}br\$ folgt. Angepasst an die gegebenen Variablen des Kegels ergeben sich die Formeln für $M_{{\mathrm {G}}}\$ und $M_{{\mathrm {H}}}\$ (siehe Zeichnung Kegelstumpf rechts, abgewickelte Mantelfläche).)

Mit Hilfe der Strahlensätze leitet man folgenden Zusammenhang innerhalb des Kegels für $s_{{\mathrm {x}}}\$ her: ${(m+s_{\mathrm {x} }) \over s_{\mathrm {x} }}={r \over R}\Leftrightarrow R(m+s_{\mathrm {x} })=rs_{\mathrm {x} }\Rightarrow s_{\mathrm {x} }={Rm \over r-R}\$ .

Durch Einsetzen von $s_{{\mathrm {x}}}\$ in $(1)\$ erhält man schließlich

${\begin{matrix}M_{\mathrm {KS} }&=&\pi (rm+r({Rm \over r-R})-R({Rm \over r-R}))\\&=&\pi (rm+{rRm \over r-R}-{{R}^{2}m \over r-R})\\&=&\pi m(r+{R(r-R) \over r-R})\\&=&\pi (r+R)m\end{matrix}}\$

Flächenberechnung mit guldinscher Regel

Mithilfe der ersten guldinschen Regel $M=L\cdot 2\pi R$ lässt sich die Fläche ebenfalls leicht ausrechnen:

ist die Länge der erzeugenden Linie (Mantellinie) und ist die Position ihres Schwerpunkts ${\frac {r_{{\mathrm {1}}}+r_{{\mathrm {2}}}}{2}}.$

Einsetzen ergibt die Mantelfläche des Kegelstumpfes $M=\pi \cdot m\cdot (r_{{\mathrm {1}}}+r_{{\mathrm {2}}}).$

Berechnung der Mantelfläche eines Rotationskörpers

Der Graph einer Funktion $f\colon [a,b]\to \mathbb{R} _{0}^{+}$ , die Mantellinie, rotiere um die x-Achse. Nun sei die Mantelfläche dieser Mantellinie im Bereich von $x_{1}=a$ bis $x_{2}=b$ gesucht.

Rotation um die x-Achse

$M=2\pi \cdot \int _{a}^{b}f(x){\sqrt {1+f'(x)^{2}}}\,{\mathrm d}x$

Erklärung:

Man stellt sich den Rotationskörper vor als zusammengesetzt aus auf der x-Achse aufgereihten Scheiben, die jede einen Kegelstumpf der Seitenlänge $\Delta L$ und den Radien $r_{1}$ und $r_{2}$ darstellen. Die Summe über die Mantelflächen der Kegelstümpfe (s.o.) bildet dann die gesamte Mantelfläche

$M=\sum _{i}\pi \cdot \Delta L_{i}\cdot (r_{{1i}}+r_{{2i}}).$

Das Linienelement $\Delta L_{i}$ der rotierenden Funktion f(x) ist über den Satz des Pythagoras gegeben als

$\Delta L_{i}={\sqrt {(\Delta x_{i})^{2}+(\Delta y_{i})^{2}}}={\sqrt {1+\left({\frac {\Delta y_{i}}{\Delta x_{i}}}\right)^{2}}}\Delta x_{i}.$

Beim Grenzübergang zum Integral (immer mehr und gleichzeitig entsprechend dünnere Kegelstumpfscheiben) werden $r_{{1i}}=r_{{2i}}=f(x_{i})$ und man kann schreiben

$M=\pi \sum _{i}2\cdot f(x_{i})\cdot {\sqrt {1+\left({\frac {\Delta y_{i}}{\Delta x_{i}}}\right)^{2}}}\Delta x_{i}\rightarrow 2\pi \cdot \int _{a}^{b}f(x){\sqrt {1+f'(x)^{2}}}\,{\mathrm d}x.$

Rotation um die y-Achse

Hier gilt demnach:

$M=2\pi \cdot \int _{{\min(f(a),f(b))}}^{{\max(f(a),f(b))}}x{\sqrt {1+(x')^{2}}}\,{\mathrm d}y$

mit $x=f^{{-1}}(y)$ , d.h. nach aufgelöst und $x'={\frac {dx}{dy}}$ .

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de