
Kugelsegment
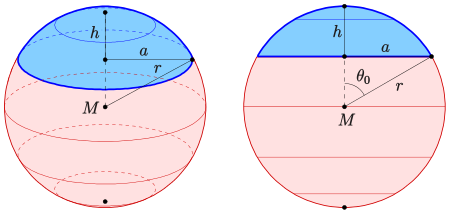
Ein Kugelsegment oder Kugelabschnitt ist ein Teil eines Kugelkörpers, der durch den Schnitt mit einer Ebene gebildet wird. Ein Kugelsegment hat die Form einer Kuppel und besitzt als Grundfläche eine Kreisscheibe. Eine Halbkugel ist ein Sonderfall eines Kugelsegments, bei der die Schnittebene den Kugelmittelpunkt enthält. Der gekrümmte Teil der Oberfläche eines Kugelsegments wird Kugelkalotte, auch Kugelkappe oder Kugelhaube genannt.
Formeln
Für die Berechnung von Volumen, Mantelfläche und Oberfläche eines
Kugelsegments gelten die folgenden Formeln. Dabei bezeichnet
den Radius der Kugel,
den Radius des Basiskreises des Kugelsegments und
die Höhe des Kugelsegments.
Diese drei Größen sind nicht unabhängig voneinander. Das Kugelsegment ist durch zwei beliebige dieser drei Größen bestimmt. Aus zwei der drei Größen lässt sich die dritte berechnen. In allen Formeln ist − bei ± zu nehmen, wenn das Kugelsegment weniger als die halbe Kugel groß ist, sonst + bei ±.
Statt
und
reicht auch die Angabe des Winkels
des Basiskreises (siehe Bild). Es gilt:
Es gibt deshalb jeweils mehrere Formeln, je nachdem, welche der Größen gegeben sind.
Volumen
Mantelfläche (Kugelkappe)
Oberfläche (inkl. Basiskreis)
Sonderfälle
Für
ist
und das Kugelsegment eine Halbkugel:
Für
ergeben sich die Formeln für die ganze Kugel:
Herleitung der Formeln
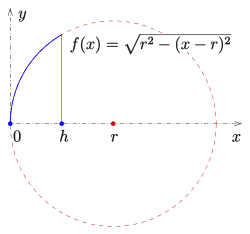
Aufgrund des Satzes von Pythagoras gilt: .
Auflösen der Klammer liefert:
.
Das Volumen eines Kugelsegments ergibt sich aus dem Volumenintegral
für Rotationskörper
für den Kreisbogen :
.
Entsprechend ergibt sich die Mantelfläche eines Kugelsegments (ohne Basiskreis) aus der Flächenformel für Rotationsflächen
.
Und mit Basiskreis: .
Ähnliche geometrische Objekte
Weitere Kugelteile sind Kugelschicht, Kugelausschnitt, Kugelring und Kugelkeil. Das zweidimensionale Analogon ist das Kreissegment.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.09. 2022