Kegel (Geometrie)

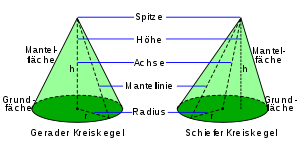
Ein Kegel oder Konus ist ein geometrischer Körper, der entsteht, wenn man alle Punkte eines in einer Ebene liegenden, begrenzten und zusammenhängenden Flächenstücks geradlinig mit einem Punkt (Spitze bzw. Apex) außerhalb der Ebene verbindet. Ist das Flächenstück eine Kreisscheibe, wird der Körper Kreiskegel genannt. Das Flächenstück nennt man Grundfläche, deren Begrenzungslinie die Leitkurve, den Punkt nennt man die Spitze oder den Scheitel des Kegels und die Fläche an der Seite wird Mantelfläche genannt. Ein Kegel hat also eine Spitze (den Scheitelpunkt), eine Kante (die Leitkurve) und zwei Flächen (die Mantel- und die Grundfläche).
Unter der Höhe des Kegels versteht man einerseits das Lot von der Spitze auf die Grundfläche (die Höhe steht also immer senkrecht zur Grundfläche), andererseits aber auch die Länge dieses Lotes (also den Abstand der Spitze von der Grundfläche).
Die Verbindungsstrecken der Spitze mit der Leitkurve heißen Mantellinien, ihre Vereinigung bildet den Kegelmantel oder die Mantelfläche.
Gerader und schiefer Kegel
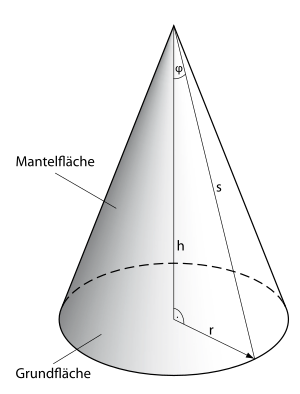
Wenn in der Geometrie von einem Kegel gesprochen wird, ist häufig der Spezialfall des geraden Kreiskegels gemeint. Unter einem Kreiskegel versteht man einen Körper, der durch einen Kreis (Grundkreis oder Basiskreis) und einen Punkt außerhalb der Ebene des Kreises (Spitze des Kegels) festgelegt ist.
Die Ebene, in welcher der Basiskreis liegt, heißt Basis(kreis)ebene. Unter
dem Radius
des Kegels versteht man normalerweise den Radius
des Basiskreises. Die Gerade
durch den Mittelpunkt des Grundkreises und die Spitze nennt man die Achse des Kegels. Die Höhe
des Kegels ist der Abstand
der Spitze von der Basisebene; dieser Abstand muss senkrecht zur
Basisebene gemessen werden.
Steht die Achse senkrecht zur Basisebene, so liegt ein gerader Kreiskegel oder Drehkegel vor. Andernfalls spricht man von einem schiefen Kreiskegel oder elliptischen Kegel. Jeder elliptische Kegel hat zwei Richtungen, in denen sein Schnitt mit einer Ebene ein Kreis ist; diese Tatsache macht sich die stereografische Projektion als Kreistreue zunutze.
Die Bezeichnung „Drehkegel“ deutet darauf hin, dass es sich um einen Rotationskörper
handelt. Er entsteht durch Rotation
eines rechtwinkligen
Dreiecks um eine seiner beiden Katheten.
In diesem Fall werden die Mantellinien (also die Verbindungsstrecken der
(Rand-)Punkte des Basiskreises mit der Spitze) auch Erzeugende genannt (),
da sie den Mantel
„erzeugen“. Der Öffnungswinkel beträgt das Doppelte des Winkels
zwischen den Mantellinien und der Achse eines Drehkegels. Der Winkel
zwischen den Mantellinien und der Achse heißt halber Öffnungswinkel.
Ein Drehkegel mit Öffnungswinkel 60° heißt gleichseitiger Kegel. Diese Bezeichnung erklärt sich wie folgt: Schneidet man einen solchen Kegel mit einer Ebene, die die Achse enthält, so erhält man ein gleichseitiges Dreieck.
Vor allem in der Technik wird für den Drehkegel auch das Wort Konus (von lat. conus) verwendet. Das zugehörige Eigenschaftswort konisch bezeichnet Objekte mit der Form eines Drehkegels oder eines (Dreh-)Kegelstumpfs.
Insbesondere im Zusammenhang mit Kegelschnitten wird das Wort „Kegel“ auch im Sinn des unten erwähnten Doppelkegels gebraucht.
Größen und Formeln
| Größen und Formeln | ||
|---|---|---|
| Radius eines geraden Kreiskegels |
||
| Höhe eines geraden Kreiskegels |
||
| Mantellinie eines geraden Kreiskegels |
||
| Halber Öffnungswinkel eines geraden Kreiskegels |
||
| Durchmesser
der Grundfläche eines geraden Kreiskegels |
||
| Grundfläche eines Kreiskegels |
||
| Flächeninhalt
der Mantelfläche eines geraden Kreiskegels |
||
| Oberfläche eines geraden Kreiskegels |
||
| Volumen eines beliebigen Kreiskegels |
||
| Trägheitsmoment eines geraden Kreiskegels (Drehung um die Symmetrieachse) |
massiver Kegel: Kegelmantel: wobei | |
Beweise
Volumen
Bereits im Jahr 1781 beschreibt Johann
Friedrich Lorenz in seiner Übersetzung Euklids Elemente Euklids Feststellung: Jeder
Kegel ist der dritte Theil eines Cylinders, welcher mit ihm einerley
Grundfläche, ABCD, und gleiche Höhe hat.
In der Elementargeometrie
wird die Volumenformel oft mit dem Prinzip
von Cavalieri begründet. Man vergleicht den gegebenen Kreiskegel mit einer
Pyramide
von gleicher Grundfläche und Höhe. Für Parallelebenen zur
Grundfläche in beliebigem Abstand
folgt aus den Gesetzen der Ähnlichkeit
bzw. der zentrischen
Streckung, dass die entsprechenden Schnittflächen gleichen Flächeninhalt
besitzen. Daher müssen die beiden Körper im Volumen übereinstimmen. Die für
Pyramiden der Grundfläche
und Höhe
gültige Volumenformel
kann daher auf den Kegel übertragen werden. Zusammen mit der Formel für die Kreisfläche erhält man
.
Es ist auch möglich, den Kegel durch eine Pyramide mit
regelmäßigem n-Eck als Grundfläche (für )
anzunähern.
Ein anderer Beweis (hier speziell für den geraden Kreiskegel dargestellt)
setzt die Integralrechnung
als Hilfsmittel ein. Es wird ein kartesisches
Koordinatensystem verwendet, wobei die Kegelspitze im Ursprung (0|0) und der
Mittelpunkt des Grundkreises im Punkt (|0)
liegen. Man kann sich nun den Kegel zusammengesetzt denken aus unendlich vielen
zylindrischen
Scheiben infinitesimaler (unendlich kleiner) Höhe (Dicke)
.
Da der Abstand einer solchen Zylinderscheibe von der Kegelspitze durch die
Koordinate
gegeben ist, gilt nach dem Strahlensatz:
- Radius eines infinitesimalen Zylinders:
- Volumen eines infinitesimalen Zylinders:
Das gesamte Volumen des Drehkegels entspricht der Gesamtheit all dieser
unendlich kleinen Zylinder. Zur Berechnung bildet man das bestimmte Integral mit
den Integrationsgrenzen 0 und :
Damit kommt man zur bekannten Formel
.
Mantelfläche
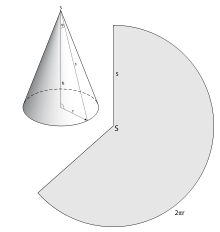
Die Mantelfläche eines geraden Kreiskegels ist gekrümmt, aber zu einem
Kreissektor abwickelbar.
Der Radius dieses Sektors stimmt mit der Länge einer Mantellinie des Kegels
()
überein. Den Mittelpunktswinkel
des Kreissektors kann man durch eine Verhältnisgleichung ermitteln. Er verhält
sich zum 360°-Winkel wie die Kreisbogenlänge
(Umfang des Basiskreises) zum gesamten Umfang eines Kreises mit Radius
:
Der gesuchte Flächeninhalt der Mantelfläche ergibt sich nun aus der Formel für den Flächeninhalt eines Kreissektors:
Die Abwicklung der Mantelfläche eines geraden Kreiskegels wird in der Darstellenden Geometrie näherungsweise mit Zirkel und Lineal durchgeführt: s. Abwicklung (Darstellende Geometrie).
Mittelpunktswinkel α
Der Mittelpunktswinkel
kann ausgehend von der Formel
berechnet werden:
ebenso
mit
= Grundflächendurchmesser,
= Mantellinie = Zeichenradius.
Doppelkegel
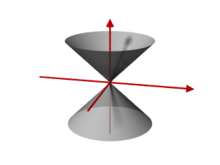
Ein Doppelkegel entsteht als Rotationsfläche einer Geraden um eine sie nicht rechtwinkelig schneidende Achse. Es entstehen zwei Drehkegel mit dem gleichen Öffnungswinkel und einer gemeinsamen Achse, die sich in der Spitze berühren. Schneidet man einen solchen unendlichen Doppelkegel mit einer Ebene, entstehen die Kegelschnitte: Kreis, Ellipse, Parabel, Hyperbel.
Analytische Beschreibung
Ein senkrechter Kreiskegel (Doppelkegel) mit der Spitze im Ursprung und der z-Achse als Symmetrieachse lässt sich durch eine Gleichung
beschreiben. Die Zahl
ist der Radius der Höhenkreise der Höhen
.
Ist
,
so vereinfacht sich die Gleichung zu
und man nennt in diesem Fall den Kegel Einheitskegel (analog zum Einheitskreis).
So, wie eine beliebige Ellipse das affine Bild des Einheitskreises ist, ist ein beliebiger Kegel (als Quadrik) das affine Bild des Einheitskegels. Die einfachsten affinen Abbildungen sind Skalierungen der Koordinaten. Skaliert man die x- und y-Achse, so ergeben sich Kegel mit Gleichungen
Die Höhenschnitte solcher Kegel sind Ellipsen. Der Schnitt mit der Höhenebene
ist die Ellipse
.
Der Kegel ist gleich der Vereinigung aller Geraden (Erzeugenden) durch die
Spitze und die Ellipsenpunkte. Beschreibt man die Ellipse
durch die Parameterdarstellung
und stellt die Erzeugenden in Parameterform dar, erhält man die folgende
Parameterdarstellung des Kegels
:
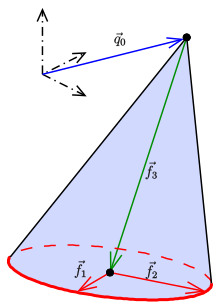
Die Gleichung eines im Raum beliebig gelagerten Kegels ist schwierig anzugeben. Die Parameterdarstellung eines beliebigen Kegels dagegen relativ einfach:
Dabei ist
die Spitze des Kegels und
sind drei linear
unabhängige Vektoren.
zeigt in Richtung der Kegelachse (s. Bild).
Für jeden konstanten Parameter
ergibt sich eine Ellipse, mit der man sich (zusammen mit der Spitze) den Kegel
erzeugt denken kann.
Sind die drei Vektoren
paarweise orthogonal und ist
,
so wird durch die Parameterdarstellung ein senkrechter Kreiskegel beschrieben.
Dass ein beliebiger elliptischer Kegel auch immer Kreise enthält, wird in Kreisschnittebene gezeigt.
Kegelkoordinaten (Koordinaten-Transformation)
Parameterdarstellung
Die Parameterdarstellung des Kegels kann man wie folgt beschreiben. Mit der
Abbildung
lassen sich die Kegelkoordinaten in kartesische Koordinaten umrechnen. Mit der
Abbildung
lassen sich die kartesischen Koordinaten in Kegelkoordinaten umrechnen.
Umrechnung eines gegebenen Kegelsegments in Kegelkoordinaten
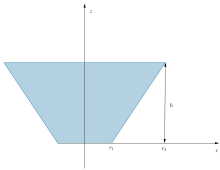
Die Parameter eines Kegelsegments seien gegeben durch (siehe nebenstehende Abbildung):
,
Dann lassen sich die Grenzen in Kegelparametern wie folgt ausdrücken:
.
Die Parameter eines soliden Kegelsegmentes bewegen sich also im Bereich:
.
Für die entsprechende Mantelfläche dieses Kegelsegmentes gilt folgende Parameterdarstellung:
.
Flächennormalenvektor
Der Flächennormalenvektor ist orthogonal zur Mantelfläche des Kegels. Er wird benötigt um z.B. Flussberechnungen durch die Mantelfläche durchzuführen. Den Flächeninhalt der Mantelfläche lässt sich als Doppelintegral über die Norm des Flächennormalenvektors berechnen.
Einheitsvektoren der Kegelkoordinaten in kartesischen Komponenten
Die Einheitsvektoren in kartesischen Komponenten erhält man durch Normierung der Tangentenvektoren der Parametrisierung. Der Tangentenvektor ergibt sich durch die erste partielle Ableitung nach der jeweiligen Variablen. Diese drei Einheitsvektoren bilden eine Normalbasis. Es handelt sich hierbei nicht um eine Orthonormalbasis, da nicht alle Einheitsvektoren orthogonal zueinander sind.
Transformationsmatrizen
Jacobi-Matrix (Funktionalmatrix)
Die Funktionalmatrix und ihre Inverse werden benötigt, um später die partiellen Ableitungen zu transformieren.
Transformationsmatrix S
Die Transformationsmatrix wird benötigt um die Einheitsvektoren und Vektorfelder zu transformieren. Die Matrix setzt sich aus den Einheitsvektoren der Parametrisierung als Spaltenvektoren zusammen. Genaueres findet man unter dem Artikel Basiswechsel.
Transformation der partiellen Ableitungen
Die partiellen Ableitungen lassen sich mit der inversen Jacobi-Matrix transformieren.
Als Ergebnis erhält man:
Transformation der Einheitsvektoren
Die Einheitsvektoren lassen sich mit der inversen Transformationsmatrix transformieren.
Als Ergebnis erhält man:
Transformation von Vektorfeldern
Vektorfelder lassen sich durch Matrixmultiplikation mit der Transformationsmatrix transformieren.
Als Ergebnis erhält man:
Oberflächen- und Volumendifferential
Das Volumendifferential lässt sich über die Determinante der Jacobi-Matrix angeben. Dies bietet die Möglichkeit z.B. das Volumen eines Kegels per Dreifachintegral zu berechnen.
Das Oberflächendifferential lässt sich mit der Norm des Flächennormalenvektors angeben. Damit kann man z.B. per Doppelintegral den Flächeninhalt der Mantelfläche bestimmen.
Transformierte Vektor-Differentialoperatoren
Nabla-Operator
Eine Darstellung des Nabla-Operators in Kegelkoordinaten erhält man, indem man die transformierten Einheitsvektoren und partielle Ableitungen in den kartesischen Nabla-Operator einsetzt:
Gradient
Den Gradienten in Kegelkoordinaten erhält man, indem man den transformieren Nabla-Operator auf ein Skalarfeld in Kegelkoordinaten anwendet.
Divergenz
Den Operator für die Divergenz eines Vektorfeldes erhält man, indem man den Nabla-Operator auf das Vektorfeld in Kegelkoordinaten anwendet:
Laplace-Operator
Der Laplace-Operator
ist die Divergenz eines Gradienten. In Kegelkoordinaten ergibt dies den
folgenden Operator:
Rotation
Die Rotation eines Vektorfeldes lässt sich als Kreuzprodukt des Nabla-Operators mit den Elementen des Vektorfelds auffassen:
Verallgemeinerungen
- Konvexe Mengen
Man verallgemeinert die Eigenschaft des (unendlichen) Kegels, aus Strahlen mit gemeinsamem Anfangspunkt zu bestehen, zu kegelförmigen Mengen, zu denen dann z.B. auch eine unendlich hohe Pyramide gehört. Besonderes Interesse gilt dabei den konvexen Kegeln, die in der linearen Optimierung eine Rolle spielen.
Dabei ist der Begriff des Ordnungskegels
wichtig: Definiert man eine Halbordnung
mittels ,
wobei
ein konvexer und abgeschlossener Kegel ist, so ist diese reflexiv,
antisymmetrisch, transitiv und multiplikativ sowie additiv verträglich. Damit
ist eine solche Halbordnung eine Verallgemeinerung der (komponentenweisen)
arithmetischen Halbordnung, der der positive Orthant
zugrunde liegt. Eine mögliche Definition eines solchen Kegels lautet:
Sei
ein reeller Banachraum und
eine nichtleere Teilmenge von
.
heißt Kegel, wenn folgende Bedingungen erfüllt sind:
ist abgeschlossen,
,
,
.
Wird die vierte Bedingung weggelassen, so erhält man eine mögliche Definition eines Keils.
Allgemeinere Grundflächen
- Als weitere Verallgemeinerung des Kegels kann man beliebige Grundflächen zulassen. Der Kegel entsteht dann als konvexe Hülle der Grundfläche und eines weiteren Punktes außerhalb der Fläche (der Kegelspitze). In diesem Sinne ist eine Pyramide ein Kegel über einem Vieleck.
- In der synthetischen Geometrie wird der Begriff Kegel für bestimmte quadratische Mengen in projektiven Geometrien beliebiger Dimension definiert. Siehe dazu Quadratische Menge#Kegel.
- Topologie
In der Topologie
versteht man unter dem Kegel über einem topologischen
Raum
den Raum, den man aus dem Produkt
durch Identifikation
aller Punkte in
(der „Kegelspitze“) erhält.
Den entsprechenden „Doppelkegel“ (durch zusätzliche Identifikation von )
bezeichnet man auch als Einhängung
oder Suspension.
Anwendungsbeispiele
Trinkglas
Einige Trinkgläser, zum Beispiel ein Martiniglas, haben annähernd die Form eines Kegels.
Ein Martiniglas mit dem Durchmesser 103 Millimeter und der Füllhöhe 59 Millimeter wird bis zum Rand mit Orangensaft gefüllt. Daraus ergeben sich das Volumen und die Mantelfläche:
- Volumen:
- Mantelfläche:
Das Martiniglas kann also mit etwa 164 Millilitern Orangensaft gefüllt werden. Die äußere Oberfläche beträgt etwa 127 Quadratzentimeter.
Weitere Beispiele
-
 Leitkegel
Leitkegel -
 Glastrichter mit eingelegtem Rundfilter
Glastrichter mit eingelegtem Rundfilter -
 Apollo-Dockingsystem
Apollo-Dockingsystem
Siehe auch
Literatur
- Rolf Baumann: Geometrie für die 9./10. Klasse. Zentrische Streckung, Satz des Pythagoras, Kreis- und Körperberechnungen. 4. Auflage. Mentor-Verlag, München 2003, ISBN 3-580-63635-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.04. 2023