Kegelstumpf
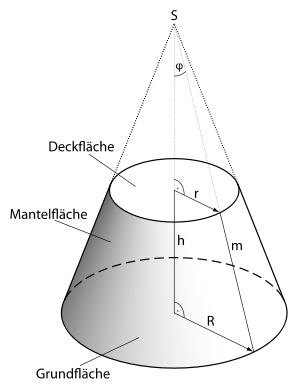
Kegelstumpf ist in der Geometrie die Bezeichnung für einen speziellen Rotationskörper. Ein Kegelstumpf entsteht dadurch, dass man von einem geraden Kreiskegel parallel zur Grundfläche einen kleineren Kegel abschneidet. Dieser kleinere Kegel wird als Ergänzungskegel des Kegelstumpfs bezeichnet.
Die größere der beiden parallelen Kreisflächen ist die
Grundfläche ,
die kleinere die Deckfläche
.
Die dritte der begrenzenden Flächen wird als Mantelfläche
bezeichnet. Diese Bezeichnungen sind zugleich für die Flächeninhalte
dieser Flächen üblich. Unter der Höhe
des Kegelstumpfs versteht man den Abstand
von Grund- und Deckfläche.
Nahe verwandt mit dem Kegelstumpf ist der Pyramidenstumpf.
Formeln
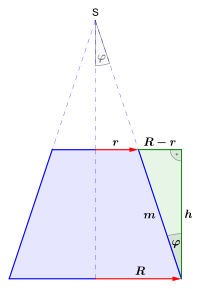
Mit
werde der Radius der Deckfläche, mit
der Radius der Grundfläche bezeichnet.
sei der Winkel zwischen einer Mantellinie und der Kegelachse.
| Formeln zum Kegelstumpf | ||
|---|---|---|
| Volumen |
 | |
| Länge einer Mantellinie | ||
| Mantelfläche | ||
| Deckfläche | ||
| Grundfläche | ||
| Oberfläche | ||
| Höhe des Kegelstumpfs | ||
Beweise
Volumen
Für die Berechnung des Volumens des Kegelstumpfs wird die Höhe des
Ergänzungskegels mit
bezeichnet. Das Volumen des Kegelstumpfs ergibt sich dann als Differenz zwischen
dem Volumen des ganzen Kreiskegels (Radius
und Höhe
)
und dem Volumen des Ergänzungskegels (Radius
und Höhe
).
Mit Hilfe des Strahlensatzes
(Vierstreckensatz) folgt, dass
.
Nennt man diesen Quotienten
,
so gilt
und
Die Höhe ist somit
Das Volumen des großen Kegels ist
das Volumen des kleinen Kegels ist
das Volumen des Kegelstumpfs ist die Differenz
Alternativ kann das Volumen eines Kegelstumpfes mithilfe eines Integrals
berechnet werden, da ein solcher Körper als ein um die x-Achse rotierter
Rotationskörper betrachtet werden kann. Die Formel zur Volumenberechnung dieser
Rotationskörper lautet: .
Setzt man hier für
ein und errechnet das Integral in den Grenzen von
und
,
so erhält man das Volumen eines Kegelstumpfes mit den entsprechenden Parametern.
Dass diese Formel der obigen Formel gleicht, ergibt sich durch folgende
Rechnung:
Mantelfläche
Für die Berechnung der Mantelfläche des Kegelstumpfs werde die Mantellinie
des abgeschnittenen kleinen Kegels mit
bezeichnet. Laut Strahlensatz gilt
,
also
.
Die Mantelfläche berechnet sich nun aus der Differenz der Mantelfläche
des großen Kegels (Radius
und Mantellinie
)
und der Mantelfläche
des kleinen weggeschnittenen Kegels (Radius
und Mantellinie
):
Oberfläche
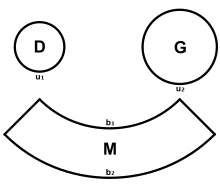
Die Oberfläche des Kegelstumpfs berechnet sich aus der Summe aus Deckfläche, Grundfläche und Mantelfläche:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.07. 2022