Pyramidenstumpf
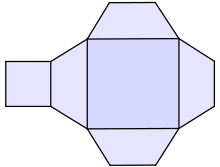
Ein Pyramidenstumpf ist ein Begriff aus der Geometrie, der einen speziellen Typ von Polyedern (Vielflächnern) beschreibt. Ein Pyramidenstumpf entsteht dadurch, dass man von einer Pyramide (Ausgangspyramide) parallel zur Grundfläche an den Mantelflächen eine kleinere, ähnliche Pyramide (Ergänzungspyramide) abschneidet.
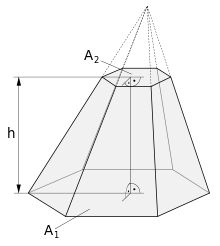
Die beiden parallelen Flächen eines Pyramidenstumpfes sind zueinander ähnlich. Die größere dieser beiden Flächen bezeichnet man als Grundfläche, die kleinere als Deckfläche. Den Abstand zwischen Grund- und Deckfläche nennt man die Höhe des Pyramidenstumpfes.
Das Volumen eines Pyramidenstumpfes kann mit Hilfe der folgenden Formel berechnet werden:
Dabei stehen A1 für die Grundfläche, A2 für die Deckfläche und h für die Höhe des Pyramidenstumpfes.
Für die aus Trapezen zusammengesetzte Mantelfläche gibt es keine einfache Formel. Je schiefer die Pyramide, bzw. der Pyramidenstumpf ist, desto größer ist die jeweils zugehörige Mantelfläche.
Beweise
Volumen
Für die Berechnung des Volumens des Pyramidenstumpfes werden
als Höhe der Ausgangspyramide und
als Höhe der Ergänzungspyramide definiert. Aus der zentrischen
Streckung folgt, dass
und daher auch
.
Dabei ist
der Streckfaktor der zentrischen Streckung.
Das Volumen des Pyramidenstumpfes ergibt sich aus der Differenz zwischen dem Volumen der Ausgangspyramide und dem Volumen der Ergänzungspyramide:
.
Aus
und
folgt
.
Die Substitution
ergibt
und
.
Damit kann man das Volumen umschreiben:
.
Mit Hilfe der Formel
angewendet auf
und
ist das Volumen
oder einfacher
.
Der Faktor
ist die Höhe
:
.
Daraus ergibt sich
.
Entartungen
- Streben Grundfläche und Deckfläche gegen einen Kreis, erhält man einen Kegelstumpf, für den dieselbe Volumenformel gilt.
- Strebt A2 gegen A1, erhält man ein Prisma, dessen Volumenformel sich durch A1 = A2 = A entsprechend vereinfacht.
- Strebt A2 gegen 0, erhält man eine Pyramide.
Literatur
- Rolf Baumann: Geometrie für die 9./10. Klasse. Zentrische Streckung, Satz des Pythagoras, Kreis- und Körperberechnungen. 4. Auflage. Mentor-Verlag, München 2003, ISBN 3-580-63635-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.05. 2021