
Divergenz eines Vektorfeldes
Die Divergenz eines Vektorfeldes ist ein Skalarfeld, das an jedem Punkt angibt, wie sehr die Vektoren in einer kleinen Umgebung des Punktes auseinanderstreben (divergere). Interpretiert man das Vektorfeld als Strömungsfeld einer Größe, für die die Kontinuitätsgleichung gilt, dann ist die Divergenz die Quelldichte. Senken haben negative Divergenz. Ist die Divergenz überall gleich null, so bezeichnet man das Feld als quellenfrei.
Die Divergenz ergibt sich aus dem Vektorfeld durch Anwendung eines Differentialoperators. Verwandte Differentialoperatoren liefern die Rotation eines Vektorfeldes und den Gradienten eines Skalarfeldes. Das mathematische Gebiet ist die Vektoranalysis.
In der Physik wird die Divergenz zum Beispiel bei der Formulierung der Maxwell-Gleichungen
oder der verschiedenen Kontinuitätsgleichungen
verwendet. Im Ricci-Kalkül
wird die mit Hilfe der kovarianten
Ableitung gebildete Größe
manchmal etwas ungenau als Divergenz eines Tensors
bezeichnet (für diese Größe gilt auf gekrümmten Mannigfaltigkeiten zum Beispiel
nicht der Gaußsche
Integralsatz).
Beispiel aus der Physik
Man betrachtet zum Beispiel eine ruhige Wasseroberfläche, auf die ein dünner Strahl Öl trifft. Die Bewegung des Öls auf der Oberfläche kann durch ein zweidimensionales (zeitabhängiges) Vektorfeld beschrieben werden: An jedem Punkt ist zu jedem beliebigen Zeitpunkt die Fließgeschwindigkeit des Öls in Form eines Vektors gegeben. Die Stelle, an der der Strahl auf die Wasseroberfläche trifft, ist eine „Ölquelle“, da von dort Öl wegfließt, ohne dass es einen Zufluss auf der Oberfläche geben würde. Die Divergenz an dieser Stelle ist positiv. Im Gegensatz dazu bezeichnet man eine Stelle, an der das Öl beispielsweise am Rand aus dem Wasserbecken abfließt, als Senke. Die Divergenz an dieser Stelle ist negativ.
Definition
Sei
ein differenzierbares Vektorfeld. Dann ist die Divergenz von
definiert als
Die Divergenz ist das Skalarprodukt
des Nabla-Operators
mit dem Vektorfeld
.
Bei der Divergenz handelt es sich um einen Operator auf einem Vektorfeld, der in einem skalaren Feld resultiert:
Für den Fall eines dreidimensionalen Vektorfeldes
ist die Divergenz in kartesischen Koordinaten definiert als
.
Bei der Schreibweise
ist es wichtig, den Multiplikationspunkt zwischen
und dem Vektorfeld
zu schreiben, da der
-Operator
sonst als Gradient
der Vektorkomponenten (geschrieben
) zu verstehen wäre.
Die Divergenz als „Quellendichte“
Interpretiert man ein Vektorfeld
als Strömungsfeld, so beschreibt dessen totales
Differenzial
ein Beschleunigungsfeld. Ist in einem Punkt
die Beschleunigungsmatrix
diagonalisierbar,
so beschreibt jeder Eigenwert
die Beschleunigung in Richtung des zugehörigen Eigenvektors
.
Jeder positive Eigenwert beschreibt also die Intensität einer gerichteten Quelle
und jeder negative Eigenwert die gerichtete Intensität einer Senke. Addiert man
diese Eigenwerte, so erhält man die resultierende Intensität einer Quelle bzw.
Senke. Da die Summe der Eigenwerte
gerade die Spur
der Beschleunigungsmatrix
ist, wird die Quellenintensität durch
gemessen.
Die Divergenz kann in diesem Sinne als „Quellendichte“ interpretiert werden.
Koordinatenfreie Darstellung
Für die Interpretation der Divergenz als „Quellendichte“ ist die folgende koordinatenfreie Definition in der Form einer Volumenableitung wichtig (hier für den Fall n=3)
Dabei ist
ein beliebiges Volumen, zum Beispiel eine Kugel oder ein Parallelepiped;
ist sein Inhalt. Es wird über den Rand
dieses Volumenelements integriert,
ist die nach außen gerichtete Normale und
das zugehörige Flächenelement. Man findet hierzu auch die Schreibweise mit
.
Für n > 3 kann diese Aussage leicht verallgemeinert werden, indem man n-dimensionale Volumina und ihre (n-1)-dimensionalen Randflächen betrachtet. Bei Spezialisierung auf infinitesimale Würfel oder Quader erhält man die bekannte Darstellung in kartesischen Koordinaten
In orthogonalen krummlinigen
Koordinaten, zum Beispiel Kugelkoordinaten
oder elliptischen
Koordinaten, (also für ,
mit
),
wobei
ist, wobei also nicht die
,
sondern die
die physikalische Dimension einer „Länge“ haben, gilt dagegen etwas allgemeiner
wobei die Punkte am Ende weitere Terme beinhalten, die durch fortgesetzte zyklische
Permutationen, erzeugt nach dem Schema
usw., aus dem angeschriebenen folgen.
Herleitung der kartesischen Darstellung
Zur Herleitung der kartesischen Darstellung der Divergenz aus der
koordinatenfreien Darstellung betrachte man einen infinitesimalen Würfel .
Nun wendet man den Mittelwertsatz
der Integralrechnung an, wobei die gestrichenen Größen
aus dem Intervall
sind.
Somit bleibt nur die Summe der Differenzenquotienten übrig
,
die im Grenzübergang
zu partiellen Ableitungen werden:
Kovariantes Verhalten bei Drehungen und Verschiebungen
Der Divergenz-Operator vertauscht mit räumlichen Drehungen und Verschiebungen eines Vektorfeldes, d.h. die Reihenfolge dieser Operationen macht keinen Unterschied.
Begründung: Wenn das Vektorfeld
im Raum gedreht oder (parallel)verschoben wird, braucht man in der oben
gegebenen koordinatenunabhängigen Darstellung nur die Flächen- und
Volumenelemente in derselben Weise zu drehen, um wieder auf denselben skalaren
Ausdruck zu kommen. Das Skalarfeld
dreht und verschiebt sich also in gleicher Weise wie das Vektorfeld
.
Ein „Zerlegungs-Theorem“
Für n=3-dimensionale Vektorfelder ,
die im ganzen Raum mindestens zweimal stetig differenzierbar sind und im
Unendlichen hinreichend rasch gegen null gehen, gilt, dass sie in einen
wirbelfreien Teil
und einen quellenfreien Teil
zerfallen,
.
Für den wirbelfreien Teil gilt, dass er durch seine Quellendichte wie folgt
dargestellt werden kann:
, mit
.
Für den quellenfreien Teil, ,
gilt analoges, wenn man das skalare Potential
durch ein sog. Vektorpotential
ersetzt und zugleich die Ausdrücke
bzw.
(=Quellendichte von
)
durch die Operationen
bzw.
(=Wirbeldichte von
)
substituiert.
Dieses Verfahren ist Bestandteil des Helmholtz-Theorems.
Eigenschaften
Im n-dimensionalen Raum
Sei
eine Konstante,
eine offene Teilmenge,
ein skalares Feld und
zwei Vektorfelder. Dann gelten folgende Regeln:
- Die Divergenz ist linear, das heißt, es gilt
und
- Für die Divergenz gilt die Produktregel
- Die Divergenz des Vektorfeldes
entspricht in beliebigen Koordinaten der Spur der kovarianten Ableitung
von
, das heißt, es gilt
.
Diese Darstellung ist koordinateninvariant, da die Spur einer linearen Abbildung invariant gegenüber einem Basiswechsel ist.
Im dreidimensionalen Raum
Ist ,
so gibt es auch eine Produktregel für das Kreuzprodukt
,
diese lautet
wobei mit
die Rotation gemeint ist. Wegen
für alle differenzierbaren
folgt daraus
für beliebige differenzierbare .
Beispiele
In kartesischen Koordinaten findet man unmittelbar
Für das Coulomb-Feld
findet man, wenn in der ersten Produktregel ,
und
gesetzt wird
Mit der Formel für die Divergenz in Kugelkoordinaten ist dieses Ergebnis ebenfalls zu erhalten.
Nach dem Korollar sind Felder
des folgenden Typs quellenfrei:
Gaußscher Integralsatz
Aussage
Eine wichtige Rolle spielt die Divergenz in der Aussage des Gaußschen Integralsatzes. Er besagt, dass der Durchfluss durch eine geschlossene Oberfläche gleich dem Integral über die Divergenz des Vektorfeldes im Inneren dieses Volumens ist, und erlaubt damit die Umwandlung eines Volumenintegrals in ein Oberflächenintegral:
wobei
der Normalenvektor der Oberfläche
ist. Anschaulich beschreibt er damit für den Fall einer Strömung den
Zusammenhang zwischen dem Durchfluss durch diese Fläche und den Strömungsquellen
und -senken innerhalb des zugehörigen Volumens.
Punktförmige Quelle
Setzt man im Gaußschen Integralsatz das coulombartige
Feld
ein und wählt man als Integrationsfläche
eine Kugelfläche mit Radius
um den Ursprung, so ist
und der Integrand wird konstant gleich
.
Weil die Oberfläche der Kugel
ist, folgt
Somit liefert der Integralsatz eine Information über ,
die im Gegensatz zu den Ableitungsausdrücken (Produktregel oder
Kugelkoordinaten) auch den Punkt
einschließt: Das Volumenintegral von
ist
.
Dies lässt sich mit dem Ergebnis der Ableitungsrechnung zu einer Distributionsgleichung
zusammenfassen:
Zylinder- und Kugelkoordinaten
In Zylinderkoordinaten
gilt für die Divergenz eines Vektorfeldes :
In Kugelkoordinaten
gilt für die Divergenz eines Vektorfeldes :
Letztere Formel kann ohne Differentiation von Basisvektoren hergeleitet
werden: Man führt eine Testfunktion
ein und schreibt ein Volumenintegral einmal in kartesischen und einmal in
Kugelkoordinaten. Mit bekannten Ausdrücken für Gradient und Volumenelement
ergibt das nach Ausmultiplizieren der Basisvektoren
Die Ableitungen von
werden partiell integriert, wobei Randterme verschwinden. Auf der rechten Seite
muss das Volumenelement mitdifferenziert und danach in zwei Termen
wiederhergestellt werden (Erweitern). Das ergibt
Aus der Gleichheit der Integrale für alle Testfunktionen folgt, dass die Ausdrücke für die Divergenz gleich sind.
Inverse
Nach dem Poincaré-Lemma existiert zu jedem Skalarfeld ein Vektorfeld, dessen Divergenz es ist. Dieses Vektorfeld ist nicht eindeutig bestimmt, denn es kann ein örtlich konstanter Vektor hinzuaddiert werden, ohne die Divergenz und damit das Skalarfeld zu verändern.
Unter gewissen Voraussetzungen existiert ein Rechts- oder Linksinverses der
Divergenz. So gibt es für ein offenes und beschränktes Gebiet
mit lipschitzstetigem
Rand einen Operator
,
so dass für jedes
mit
gilt, wobei
den entsprechenden Sobolew-Raum
für
und
bezeichnet.
heißt Bogowskii-Operator.
Divergenz auf riemannschen Mannigfaltigkeiten
Im Abschnitt Eigenschaften wurde bereits gesagt, dass die Divergenz mit Hilfe der Spur der Jacobimatrix ausgedrückt werden kann und dass diese Darstellung koordinateninvariant ist. Aus diesem Grund verwendet man diese Eigenschaft, um die Divergenz auf riemannschen Mannigfaltigkeiten zu definieren. Mit Hilfe dieser Definition kann man zum Beispiel den Laplace-Operator auf riemannschen Mannigfaltigkeiten koordinatenfrei definieren. Dieser heißt dann Laplace-Beltrami-Operator.
Definition
Sei
eine riemannsche Mannigfaltigkeit und
ein
-Vektorfeld mit
.
Dann ist die Divergenz durch
definiert. Dabei ist
ein Vektorfeld und der Operator
ist der Levi-Civita-Zusammenhang,
der den Nabla-Operator verallgemeinert. Wertet man
an
aus, so ist
und man kann für alle
die aus der linearen Algebra bekannte Spur bilden.
Transportsatz und geometrische Interpretation
Für den Fluss
eines Vektorfeldes
gilt der Transportsatz
Dabei ist
das Riemann-Lebesguesche
Volumenmaß auf der Mannigfaltigkeit,
eine relativ-kompakte
messbare
Teilmenge und
eine glatte
Funktion. Interpretiert man
als Dichte
einer Erhaltungsgröße,
dann folgt daraus die Kontinuitätsgleichung.
Für
erhält man
Die Divergenz ist also die Dichte der Volumenänderungsrate bezüglich des Flusses. Die Divergenz in einem Punkt gibt an, wie schnell sich der Inhalt eines infinitesimalen Volumenelements in diesem Punkt ändert, wenn es sich mit dem Fluss bewegt. Als Folgerung ergibt sich, dass ein Vektorfeld genau dann divergenzfrei ist, wenn der erzeugte Fluss volumenerhaltend ist.
Divergenz von Tensoren zweiter Stufe
In den Ingenieurwissenschaften wird die Divergenz auch für Tensoren zweiter Stufe eingeführt und liefert dann Vektorfelder. Zum Beispiel geht die Divergenz des Spannungstensors in die lokale Impulsbilanz der Kontinuumsmechanik, das erste Cauchy-Eulersche Bewegungsgesetz, ein.
Definition
Tensoren zweiter Stufe bilden Vektoren auf Vektoren ab. Indem die vektorielle Divergenz mit der Divergenz des Tensors in Zusammenhang gebracht wird, kann die Divergenz auf Tensoren T verallgemeinert werden:
Darin bildet das Superskript ⊤ den transponierten Tensor. Mit dem Nabla-Operator berechnet sich diese Divergenz mittels
In der Literatur insbesondere der Strömungsmechanik
wird auch die transponierte Version
benutzt.
Komponenten der Divergenz eines Tensors
Divergenz eines Tensors in kartesischen Koordinaten
Für einen Tensor
ergibt sich bezüglich der Standardbasis
ê1,2,3 eines kartesischen
Koordinatensystems mit x-, y- und z-Koordinaten, die gemäß dem Schema
x → 1, y → 2 und z → 3 nummeriert werden:
Die transponierte Version
ergibt sich hieraus duch Vertauschen von Tab durch
Tba.
Divergenz eines Tensors in Zylinderkoordinaten
In Zylinderkoordinaten mit Basisvektoren
ergibt sich die Divergenz für Tensoren zweiter Stufe zu
Ein Index hinter einem Komma bezeichnet hier die Ableitung nach der
Koordinate: .
Die transponierte Version
ergibt sich hieraus durch Vertauschen von Tab durch
Tba.
Divergenz eines Tensors in Kugelkoordinaten
In Kugelkoordinaten mit Basisvektoren
ergibt sich die Divergenz für Tensoren zweiter Stufe zu
Ein Index hinter einem Komma bezeichnet hier die Ableitung nach der
Koordinate: .
Die transponierte Version
ergibt sich hieraus durch Vertauschen von Tab durch
Tba.
Eigenschaften
Im n-dimensionalen Raum
Sei
eine Konstante,
eine offene Teilmenge,
ein skalares Feld,
zwei Vektorfelder und T ein tensorielles Feld. Dann gelten folgende
Regeln:
Darin ist
das Frobenius-Skalarprodukt
für Vektoren bzw. Tensoren und eine Ableitung nach der Koordinate xi
in einem kartesischen Koordinatensystem mit Basisvektoren
wird mit einem Index ,i abgekürzt, über den des Weiteren oben von
eins bis drei zu summieren ist (Einsteinsche
Summenkonvention).
Im dreidimensionalen Raum
Für die Herleitung des zweiten Cauchy-Euler’schen Bewegungsgesetzes, das die Erhaltung des Drehimpulses in einem Kontinuum sicherstellt, wird die Produktregel
gebraucht. Darin sind
ein vektorielles und T ein tensorielles, differenzierbares Feld und
bildet die Vektorinvariante.
Gaußscher Integralsatz
Dieser Integralsatz wird in der Kontinuumsmechanik auch für Tensorfelder,
z.B. von Spannungstensoren
,
benötigt:
Der vom symmetrischen
Spannungstensor transformierte Normalenvektor
an die Fläche ist nach dem Cauchy’schen
Fundamentaltheorem der auf der Fläche wirkende Spannungsvektor
(ein Vektor mit der Dimension Kraft pro Fläche). Diese Gleichung ist im Fall
ihres Verschwindens bereits die Impulsbilanz deformierbarer Körper im statischen
Fall in Abwesenheit einer Volumenkraft.
Expansionsrate
Die Divergenz eines Vektorfeldes
lautet in diesem Formalismus:
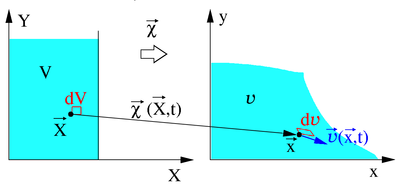
Ist speziell
das Geschwindigkeitsfeld einer Bewegung
(Bildraum) von Punkten
aus einem zeitunabhängigen Volumen V (Urbildraum), siehe Bild, dann ist der
Gradient des Vektorfeldes der Geschwindigkeitsgradient
l
der mit der Zeitableitung des Deformationsgradienten F und seiner Inversen zusammenhängt. Die Determinante des Deformationsgradienten transformiert die Volumenformen (rot im Bild) ineinander:
Zeitableitung dieser Gleichung ergibt mit dem Frobenius-Skalarprodukt „:“ (siehe Ableitungen der Hauptinvarianten)
denn die Volumenform im Urbildraum ist nicht von der Zeit abhängig. Wenn die Divergenz verschwindet, dann ist die Bewegung lokal volumenerhaltend. Eine positive Divergenz bedeutet Expansion, was in der Realität mit einer Abnahme der Dichte einhergeht.
Literatur
- Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
- H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.01. 2021