Cauchy-eulersche Bewegungsgesetze
Die Cauchy-Euler’schen Bewegungsgesetze von Augustin-Louis Cauchy und Leonhard Euler sind die lokalen Formen der Impuls- und Drehimpulsbilanz in der Kontinuumsmechanik. Es sind Bewegungsgleichungen, die, wenn sie in jedem Punkt eines Körpers erfüllt sind, sicherstellen, dass die Bewegung des Körpers als Ganzes – inklusive Verformungen – der Impuls- bzw. Drehimpulsbilanz gehorcht.
Das erste Cauchy-Euler’sche Bewegungsgesetz korrespondiert mit der Impulsbilanz und lautet im geometrisch linearen Fall an einem materiellen Punkt des Körpers:
Hier ist ρ die Dichte,
die Beschleunigung
des materiellen Punktes,
die Schwerebeschleunigung,
der Cauchy’sche Spannungstensor
und div der Divergenzoperator.
Die spezifische Impulsänderung bestimmt sich demnach aus der spezifischen
Schwerkraft und dem Antrieb durch die Spannungen. Alle Variablen in der
Gleichung sind im Allgemeinen sowohl vom Ort als auch von der Zeit abhängig.
Das zweite Cauchy-Euler’sche Bewegungsgesetz entspricht der lokalen Drehimpulsbilanz, die sich auf die Forderung nach der Symmetrie des Cauchy’schen Spannungstensors reduziert:
Das Superskript „┬“ markiert die Transposition. Die Symmetrie bedeutet, dass die Scherspannungen in einer Ebene genauso groß sind wie in dazu senkrechten Ebenen.
Bei großen Verschiebungen können beide Bewegungsgesetze in lagrangescher Betrachtungsweise materiell oder eulerscher Betrachtungsweise räumlich formuliert werden. Die Struktur der Gleichungen bleibt dabei erhalten aber es kommt zu Modifikationen in den Abhängigkeiten oder im Spannungstensor. Für Begriffsklärung empfiehlt sich die Lektüre des Artikels zur Kontinuumsmechanik.
Die Cauchy-Euler’schen Bewegungsgesetze sind die Basis für die Euler’schen Gleichungen der Strömungsmechanik, der Navier-Stokes-Gleichungen und der Navier-Cauchy-Gleichungen. Eine der Grundgleichungen der Verschiebungsmethode in der Finite-Elemente-Methode ist das Prinzip von d’Alembert in der Lagrange’schen Fassung, das eine zum ersten Cauchy-Euler’schen Gesetz äquivalente Aussage ist.
Erstes Cauchy-Euler’sches Bewegungsgesetz
Das erste Cauchy-Euler’sche Bewegungsgesetz folgt aus dem 1687 von Isaac Newton formulierten und nach ihm benannten zweiten Newton’schen Gesetz, das der Impulsbilanz entspricht, dergemäß die Änderung des Impulses mit der Zeit gleich der auf einen Körper wirkenden äußeren Kräfte ist:
Der Vektor
stellt den Impuls
dar, dessen zeitliche Änderung sich aus volumenverteilten und oberflächig
eingeleiteten Kräften
bzw.
ergibt. In dem die Kontinuumsmechanik den Körper als Punktmenge idealisiert,
wird aus der obigen Gleichung eine Integralgleichung
in der der spezifische Impuls, die spezifische Schwerebeschleunigung und die
oberflächig wirkenden Kräfte über das Volumen bzw. über die Oberfläche
integriert werden. Bei kleinen Verformungen kann das erste Cauchy-Euler’sche
Bewegungsgesetz am Volumenelement hergeleitet werden.
Impulsbilanz am Volumenelement
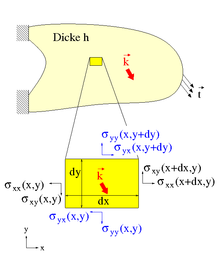
Der zweidimensionalen Fall im ebenen Spannungszustand
lässt sich leichter
veranschaulichen und soll daher vorangestellt werden. Dazu wird eine ebene
Scheibe der Dicke h betrachtet, die durch in der Ebene wirkende Kräfte belastet
wird, siehe oberen Bildteil. Aus dieser Scheibe wird gedanklich ein rechteckiges
Stück (gelb) herausgeschnitten, parallel zu dessen Kanten ein kartesisches
Koordinatensystem definiert wird in dem es die Breite dx und Höhe dy hat. Nach
dem Schnittprinzip entstehen an den Schnittflächen Schnittspannungen, die an die
Stelle des weggeschnittenen Teils treten. Bei einem (infinitesimal) kleinen
Scheibenelement können die Schnittspannungen als über die Fläche konstant
angenommen werden. Die Schnittspannungen
treten auf der Oberfläche mit der Normalen in x-Richtung auf und entsprechend
operiert
auf der Oberfläche mit der Normalen in y-Richtung. In der Komponente
bezieht sich der erste Index also auf die Flächennormale und der zweite Index
auf die Wirkrichtung. Nach Voraussetzung gibt es keine Spannungen senkrecht zur
Scheibenebene. An den Flächen, deren Normalen in positive Koordinatenrichtung
weisen, ist das positive Schnittufer und die Spannungen wirken in
positiver Richtung. An den Flächen, deren Normalen in negative
Koordinatenrichtung weisen, ist das negative Schnittufer und die
Spannungen wirken in negativer Richtung, siehe Bild.
Das zweite Newton’sche Gesetz besagt, dass die an dem Scheibenelement angreifenden Spannungen – multipliziert mit ihrer Wirkfläche – das Scheibenelement beschleunigen. An dem Scheibenelement führt das unter Berücksichtigung der Schwerebeschleunigung in x- und y-Richtung auf
Die Masse dm=ρ h dx dy des Scheibenelements ergibt sich aus der Dichte ρ des
Materials und dem Volumen h dx dy. Division durch dieses Volumen liefert im
Grenzwert
und
die lokale Impulsbilanz in x- bzw. y-Richtung:
wenn – wie üblich – die Koordinaten nach dem Schema x→1, y→2, z→3 durchnummeriert werden. In drei Dimensionen resultieren die gleichen Differentialgleichungen analog, nur wird von eins bis drei summiert:
Multiplikation dieser Gleichungen mit dem Basisvektor
der Standardbasis und
Addition der resultierenden drei Gleichungen mündet in der Vektorgleichung
Der Nabla-Operator
„“
liefert im Skalarprodukt
die Divergenz div des Cauchy’schen Spannungstensors
,
der eine Summe von Dyaden ist, die mit dem dyadischen
Produkt „
“
der Basisvektoren und seinen Komponenten
gebildet werden. Die Vektorgleichung ist die koordinatenfreie Version der
lokalen Impulsbilanz, die in beliebigen Koordinatensystemen gilt.
Der Schnittspannungsvektor
in der Schnittfläche mit Normalenvektor in x-Richtung ist im Cauchy’schen Spannungstensor zeilenweise eingetragen, was sinngemäß auch für Schnittspannungsvektoren in y- und z-Richtung gilt.
Impulsbilanz in lagrangescher Fassung
In der lagrangeschen Fassung lautet die globale Impulsbilanz
die den materiellen Punkten (Partikel) zugeordnete physikalische Größen
benutzt, siehe Impulsbilanz.
Die Partikel werden durch ihre materiellen Koordinaten
in dem Volumen V des Körpers zu einer festgelegten Zeit t0 im
Referenzzustand identifiziert. Die einem materiellen Punkt zugeordnete
Dichte ρ0 ist auf Grund der Massenbilanz
keine Funktion der Zeit. Der aufgesetzte
Punkt steht hier wie im Folgenden für die substantielle
Ableitung, also für die Zeitableitung bei festgehaltenem Partikel, was auch
den Operator
definiert:
Bei dem Integral oben soll die substantielle Ableitung bedeuten, dass das Integrationsgebiet bei der Zeitableitung als materielles behandelt wird, sich also mit dem Körper mitbewegt, ohne dass neue Partikel zum Gebiet hinzukommen oder wegfallen.
Weil das Referenzvolumen V somit nicht von der Zeit abhängt, kann die Zeitableitung des Integrals in den Integranden verschoben werden:
Die von außen angreifenden, flächenverteilten Kräfte (Spannungen)
sind die mit dem Nominalspannungstensor N transformierten
Normalenvektoren
an der Oberfläche A des Körpers:
.
Das Oberflächenintegral dieser Oberflächenspannungen wird mit dem Gauß’schen
Integralsatz in ein Volumenintegral umgewandelt:[F 1]
Der Divergenzoperator DIV wird hier groß geschrieben, weil er die materiellen
Ableitungen nach den materiellen Koordinaten
beinhaltet und vom räumlichen Operator div zu unterscheiden ist, der die
räumlichen Ableitungen nach den räumlichen Koordinaten
ausführt und der in der eulerschen Fassung benötigt wird. Mit den vorliegenden
Ergebnissen kann die Impulsbilanz als verschwindendes Volumenintegral
ausgedrückt werden:
Diese Gleichung gilt für jeden Körper und jeden seiner Teilkörper, so dass – Stetigkeit des Integranden vorausgesetzt – auf das erste Cauchy-Euler’sche Bewegungsgesetz in der lagrangeschen Fassung
geschlossen werden kann. Das Vorkommen der materiellen Koordinaten und des
Nominalspannungstensors N an Stelle des Cauchy’schen Spannungstensors
berücksichtigt die Formänderung des bei der Betrachtung am Volumenelement oben
herausgeschnitten Teilkörpers bei großen Deformationen. Bei kleinen
Verschiebungen ist
und zwischen den materiellen und räumlichen Koordinaten braucht nicht
unterschieden zu werden, wodurch das eingangs angegebene Bewegungsgesetz
entsteht.
Impulsbilanz in eulerscher Fassung
In der eulerschen Fassung lautet die globale Impulsbilanz
Die räumlichen Punkte werden durch ihre räumlichen Koordinaten
in dem momentanen Volumen v zur Zeit t identifiziert, siehe Impulsbilanz.
Anders als in der lagrangeschen Fassung sind die Integrationsgrenzen als
Oberflächen des Körpers von der Zeit abhängig, was bei der Berechnung der
Impulsänderung zu berücksichtigen ist. Nach dem Reynolds’schen
Transportsatz gilt:
Der aufgesetzte Punkt steht für die substantielle Ableitung und der
unterklammerte Term trägt auf Grund der lokalen Massenbilanz
in der eulerschen Fassung nichts bei. Das Oberflächenintegral der von außen
angreifenden Spannungen wird wie in der lagrangschen Fassung mit dem Gauß’schen
Integralsatz in ein Volumenintegral überführt:
Mit den vorliegenden Ergebnissen kann die Impulsbilanz als verschwindendes Volumenintegral ausgedrückt werden:
Diese Gleichung gilt für jedes Volumen, so dass – Stetigkeit des Integranden vorausgesetzt – das erste Cauchy-Euler’sche Bewegungsgesetz in der eulerschen Fassung
abgeleitet werden kann. Hier ist die substantielle Zeitableitung der
Geschwindigkeit bei festgehaltenem Partikel ,
das sich zur Zeit t am Ort
befindet und die Geschwindigkeit
besitzt, zu bilden:[F 2]
Der räumliche Operator grad berechnet den räumlichen Geschwindigkeitsgradienten
mit Ableitungen nach den räumlichen Koordinaten x1,2,3. Der konvektive Anteil
in der substantiellen Beschleunigung berücksichtigt das Hindurchfließen des
Materials durch das bei der Betrachtung am Volumenelement oben festgehaltene
Volumen v bei großen Verschiebungen. Bei kleinen Verschiebungen kann dieser
quadratische konvektive Anteil vernachlässigt werden, so dass mit
das eingangs angegebene Bewegungsgesetz entsteht.
Einfluss von Sprungstellen in der Impulsbilanz
Die verlangte örtliche Stetigkeit der Integranden wird unter realen
Verhältnissen verletzt, wenn beispielsweise Dichtesprünge
an Materialgrenzen oder Stoßwellen
auftreten. Solche flächigen Sprungstellen können jedoch berücksichtigt werden,
wenn die Fläche selbst örtlich stetig differenzierbar ist und so in jedem ihrer
Punkte einen Normalenvektor
besitzt. Die Fläche – im Folgenden Sprungstelle genannt – muss keine materielle
Fläche sein, kann sich also mit einer anderen Geschwindigkeit bewegen als die
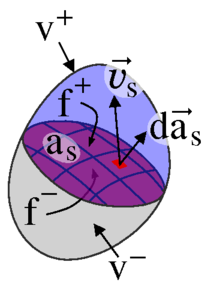
Masse selbst. Durch diese Fläche wird die Masse in zwei Stücke v+ und
v− geteilt und es wird vereinbart, dass der Normalenvektor der
Sprungstelle as in Richtung der Sprungstellengeschwindigkeit
und das Volumen v+ weise, siehe Bild rechts.
Dann lautet das Reynolds-Transport-Theorem mit Sprungstelle:
Der zweite Term mit der Sprungklammer [[...]] kommt neu hinzu. Die Integrale über die von außen angreifenden Kräfte werden getrennt für die Volumina v+ und v− berechnet:
Die Normale soll immer nach außen gerichtet sein und geht daher auf der Sprungstelle einmal mit positivem und einmal mit negativem Vorzeichen ein. Die Vereinigung der Oberflächen a+ und a− ergibt die Oberfläche a des gesamten Volumens v, zu dessen Oberfläche die innere Fläche as nicht gehört. Die Summe der drei Gleichungen führt nach Umformungen, wie sie oben bereits angegeben wurden, auf
Jenseits der Sprungstelle verschwindet die rechte Seite und die lokale Impulsbilanz ohne Sprungstelle folgt. An der (flächigen) Sprungstelle ist dv=0 und die linke Seite kann vernachlässigt werden, so dass bei Stetigkeit des Integranden mit der Sprungklammer in der Fläche
abgeleitet werden kann. Wenn die Sprungstelle eine materielle Fläche ist, wie
beispielsweise zwischen zwei aneinander grenzenden Materialien unterschiedlicher
Dichte, dann ist
und es folgt:
Die Schnittspannungen auf beiden Seiten einer materiellen Sprungstelle müssen gleich sein.
Zweites Cauchy-Euler’sches Bewegungsgesetz
Das zweite Cauchy-Euler’sche Bewegungsgesetz folgt aus dem 1754 von Leonhard
Euler aufgestellten und nach ihm benannten eulerschen
Drehimpulssatz, nach dem die zeitliche Änderung des Drehimpulses
gleich der von außen angreifenden Drehmomente
ist:
Der Vektor
steht für das von volumenverteilten Kräften ausgehende Drehmoment und der Vektor
für das oberflächig eingeleitete Moment.
Drehimpulsbilanz am Volumenelement
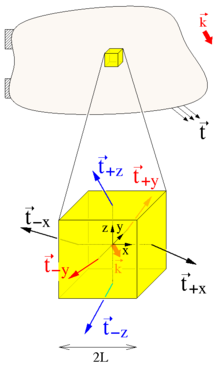
Es wird ein belasteter Körper betrachtet, aus dem gedanklich ein
würfelförmiger Teilkörper (im Bild gelb) herausgeschnitten wird, der die
Kantenlänge 2L hat und in dessen Schwerpunkt ein zu den Würfelkanten parallel
ausgerichtetes kartesisches Koordinatensystem gelegt wird. An den Würfelflächen
entstehen dem Schnittprinzip zufolge Schnittspannungen ,
die an die Stelle des weggeschnittenen Teilkörpers treten und die nach dem
Cauchy’schen
Fundamentaltheorem die mit dem Cauchy’schen Spannungstensor transformierten
Normalenvektoren an die Schnittfläche sind. Bei infinitesimal kleinem Würfel
können die Schnittspannungen als über die Fläche konstant angenommen werden und
zu einer Resultierenden aufintegriert werden, die den Würfel aus
Symmetriegründen in den Flächenmitten belasten. Für die in der Würfelmitte
angreifenden Momente gilt:
- Vom Schwerpunkt des Würfels weist der Vektor
zur Mitte der Schnittfläche am positiven Schnittufer mit Normale in +x-Richtung und die Schnittspannung
wirkt dort auf der Fläche 4L².
- Das Moment der Schnittspannung am positiven Schnittufer lautet damit:
. Das Rechenzeichen „ד bildet das Kreuzprodukt.
- Am negativen Schnittufer ist der Hebelarm
und die Schnittspannung
operiert auf der gleichen Fläche 4L²:
.
- Die Momente der Schnittspannungen summieren sich zu
.
- In den anderen beiden Raumrichtungen ergibt sich entsprechend
und
.
- Im infinitesimal kleinen Würfel kann von ortunabhängiger Dichte ρ und ortsunabhängigem Schwerefeld ausgegangen werden, das daher in der Würfelmitte kein Moment verursacht.
Die konstante Dichte hat den Trägheitstensor
zur Folge, der proportional zum Einheitstensor
I ist und die Winkelbeschleunigung
in die Änderung des Drehimpulses transformiert:
.
Diese Rate ist gemäß der eulerschen
Gleichungen der Kreiseltheorie gleich der Summe der Momente:
Division durch das Volumen L³ führt im Grenzwert L → 0 auf
und somit
Die Summe kann mit dem Skalarkreuzprodukt „“
von Tensoren[F 3] koordinatenfrei ausgedrückt werden:
Bei einem nicht würfelförmigen Quader mit unterschiedlichen Dimensionen in
x-, y- und z-Richtung resultiert ebenfalls ,
so dass die Symmetrie
des Cauchy’schen Spannungstensors folgt:
Diese Tensorgleichung ist die koordinatenfreie Version der lokalen Drehimpulsbilanz, die in beliebigen Koordinatensystemen gilt.
Drehimpulsbilanz in lagrangescher Fassung
Der Drehimpulssatz lautet in globaler lagrangescher Formulierung:
Der Vektor
ist ein beliebiger, zeitlich fixierter Ortsvektor, siehe Drehimpulsbilanz.
Die Zeitableitung des ersten Integrals kann wie bei der Impulsbilanz in den
Integranden verschoben werden:
wobei die Argumentenliste der Funktionen der Übersichtlichkeit halber weggelassen wurde. Das Oberflächenintegral wird wie gehabt mit dem Gauß’schen Integralsatz in ein Volumenintegral umgeschrieben:
Hier wurde die Produktregel
und die Definition des Deformationsgradienten
eingesetzt. Der Operator GRAD bildet den materiellen Gradienten mit
Ableitungen nach den materiellen Koordinaten X1,2,3, weshalb der
Operator hier in Abgrenzung zum räumlichen Gradienten grad groß geschrieben
wird.
Mit den vorliegenden Ergebnissen kann die Drehimpulsbilanz als verschwindendes Volumenintegral ausgedrückt werden:
Der unterklammerte Term trägt wegen der lokalen Impulsbilanz nichts bei. Das
letzte Integral gilt für jeden beliebigen Teilkörper, so dass bei stetigem
Integrand
und – wie bei der Herleitung am Volumenelement – die Symmetrie von
abgeleitet werden kann. Die lokale Drehimpulsbilanz in der lagrangeschen Fassung
reduziert sich demnach auf die Forderung
Multiplikation von links mit
und von rechts mit
ergibt gleichbedeutend:
Der Tensor
ist der zweite Piola-Kirchhoff’sche Spannungstensor, dessen Symmetrie gemäß
die Erfüllung der Drehimpulsbilanz sicherstellt. Bei kleinen Verschiebungen
stimmen der zweite Piola- Kirchhoff’sche und der Cauchy’sche Spannungstensor
näherungsweise überein: .
Drehimpulsbilanz in eulerscher Fassung
In globaler eulerscher Formulierung lautet der Drehimpulssatz:
Wie in der lagrangeschen Fassung ist
ist ein beliebiger, zeitlich fixierter Ortsvektor, siehe Drehimpulsbilanz.
Die räumlichen Koordinaten
stellen Integrationsvariable dar, die daher nicht von der Zeit abhängen. Das
erste Integral wird wie bei der Impulsbilanz mit dem Reynolds’schen
Transportsatz berechnet:
Der unterklammerte Term trägt auf Grund der Massenbilanz nichts bei. Das Oberflächenintegral in der Drehimpulsbilanz wird analog zur lagrangeschen Fassung mit dem Gauß’schen Integralsatz in ein Volumenintegral umgeschrieben:
Abweichend von der lagrangeschen Fassung tritt hier der Cauchy’sche
Spannungstensor an die Stelle des Nominalspannungstensors und wegen
der Einheitstensor an die Stelle des Deformationsgradienten.
Mit den vorliegenden Ergebnissen kann die Drehimpulsbilanz als verschwindendes Volumenintegral ausgedrückt werden:
Der unterklammerte Term trägt wegen der lokalen Impulsbilanz nichts bei und
das letzte Integral gilt für jedes beliebige Volumen, so dass bei stetigem
Integrand auf
geschlossen werden kann. Analog zur lagrangeschen Fassung reduziert sich die
Drehimpulsbilanz in eulerscher Fassung auf die Forderung nach der Symmetrie des
Cauchy’schen Spannungstensors:
Einfluss von Sprungstellen in der Drehimpulsbilanz
Analog zum ersten Cauchy-Euler’schen Bewegungsgesetz lautet das Reynolds-Transport-Theorem mit Sprungstelle hier:
Der zweite Term mit der Sprungklammer [[...]] kommt neu hinzu. Die Integrale über die von außen angreifenden Kräfte werden getrennt für v+ und v− berechnet:
Die Summe der drei Gleichungen führt nach Umformungen, wie sie oben bereits angegeben wurden, auf
Jenseits der Sprungstelle verschwindet die rechte Seite und die Symmetrie des Spannungstensors folgt wie oben. An der (flächigen) Sprungstelle ist dv=0 und die linke Seite kann vernachlässigt werden, so dass bei Stetigkeit des Integranden mit der Sprungklammer in der Fläche
abgeleitet werden kann, was wegen der Sprungbedingung im ersten Cauchy-Euler’schen Bewegungsgesetz identisch erfüllt ist.
Folgerungen aus den Bewegungsgesetzen
Aus den Bewegungsgesetzen können weitere, materialunabhängige, zu Prinzipien äquivalente Gleichungen gefolgert werden. Das erste Cauchy-Euler’sche Bewegungsgesetz lautet:
Diese Gleichungen werden mit einem Vektorfeld
skalar multipliziert und über das Volumen des Körpers integriert. Es
entsteht:
Je nach Vektorfeld
ergeben sich verschiedene Aussagen.
| Beweis |
| Skalare Multiplikation des ersten Cauchy-Euler’schen Bewegungsgesetzes
mit dem Vektorfeld
Im letzten Schritt wurde ausgenutzt, dass im Skalarprodukt mit einem
symmetrischen Tensor
|
Prinzip von d’Alembert
Das Prinzip von d’Alembert hat eine grundlegende Bedeutung für die Lösung von
Anfangsrandwertaufgaben der Kontinuumsmechanik, insbesondere der
Verschiebungsmethode
in der Finite-Elemente-Methode.
Für das Vektorfeld
werden virtuelle Verschiebungen
eingesetzt, die vom Verschiebungsfeld
unabhängige, gedachte, weitgehend beliebige, differenzielle Verschiebungen sind
und die mit den geometrischen Bindungen des Körpers verträglich sind. Die
virtuellen Verschiebungen müssen verschwinden, wo immer
Verschiebungsrandbedingungen des Körpers vorgegeben sind. Sei
der Teil der Oberfläche
des Körpers, auf dem Verschiebungsrandbedingungen erklärt sind. Für ein
Vektorfeld der virtuellen Verschiebungen
ist dann
zu fordern. Auf
können dann keine Oberflächenspannungen vorgegeben werden. Deshalb bezeichnet
den Teil der Oberfläche des Körpers, auf dem Oberflächenspannungen wirken
(können) was entsprechend auch in der räumlichen Formulierung definiert wird. So
entsteht:
Die Menge
enthält alle zulässigen, materiellen bzw. räumlichen, virtuellen
Verschiebungsfelder. Auf der linken Seite steht die virtuelle Arbeit der
Trägheitskräfte und die virtuelle Deformationsarbeit und auf der rechten Seite
die virtuelle Arbeit der äußeren Kräfte (volumen- und oberflächenverteilt.)
In der materiellen Fassung stehen die virtuelle Verzerrungen
für die Variation des Green-Lagrange’schen Verzerrungstensors:
Darin ist
der virtuelle Deformationsgradient. In der räumlichen Fassung bildet sich der
virtuelle Verzerrungstensor
aus dem virtuellen Verschiebungsgradient
:
Bilanz der mechanischen Energie
Wenn für
das Geschwindigkeitsfeld eingesetzt wird, folgt die Bilanz der mechanischen
Energie:
Auf der linken Seite steht die zeitliche Änderung der kinetischen Energie und auf der rechten Seite steht die Leistung der äußeren Kräfte (volumen- und flächenverteilt) abzüglich der Verformungsleistung. Dieser Satz wird auch Arbeitssatz genannt.
| Beweis |
| Die Zeitableitung der kinetischen Energie ist gleich der Leistung der
Trägheitskräfte
Die Leistungen der äußeren Kräfte ergeben sich durch Ersetzung des
Vektors |
Energieerhaltungssatz
In einem konservativen System gibt es eine skalarwertige Funktion Wa, die potentielle Energie, deren negative Zeitableitung gemäß
die Leistung der äußeren Kräfte ist, und eine Formänderungsenergie Wi, deren Zeitableitung
die Verformungsleistung ist. Mit der Abkürzung
für die kinetische Energie schreibt sich die Bilanz der mechanischen Energie:
Die mechanische Gesamtenergie E, bestehend aus der kinetischen Energie, der Formänderungsenergie und der potentiellen Energie, ist mithin in einem konservativen System zeitlich konstant, was als Energieerhaltungssatz bekannt ist.
Satz von Clapeyron
Wird bei kleinen Verformungen, linearer Elastizität und im statischen Fall
für das Vektorfeld
das Verschiebungsfeld
eingesetzt, dann ist
der Verschiebungsgradient
und
so dass alle Terme, die
in höherer Ordnung als eins enthalten, vernachlässigt werden können. Es
folgt:
Der symmetrische Anteil des Verschiebungsgradienten ist der linearisierte Verzerrungstensor. Der zweite Piola-Kirchhoff’sche Spannungstensor geht bei kleinen Verformungen in den Cauchy’schen Spannungstensor über und es resultiert der Arbeitssatz
Der Integrand auf der linken Seite ist das doppelte der Formänderungsenergie
und es entsteht der Satz von Clapeyron
Anmerkungen
- ↑
In der Literatur wird auch der erste
Piola-Kirchhoff’sche Spannungstensor
und eine abweichende Definition der Divergenz eines Tensors benutzt:
Dann ist.
- ↑
Die Fréchet-Ableitung
einer Funktion
nach
ist der beschränkte lineare Operator
der – sofern er existiert – in alle Richtungen
dem Gâteaux-Differential entspricht, also
gilt. Darin istskalar-, vektor- oder tensorwertig aber
und
gleichartig. Dann wird auch
geschrieben. - ↑
Das Skalarkreuzprodukt von Tensoren ist mit
Vektoren
und dem dyadischen Produkt „
“ definiert über
Das Skalarkreuzprodukt des Einheitstensors mit einer Dyade vertauscht das dyadische Produkt durch das Kreuzprodukt:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.02. 2021