Bewegungsgleichung

Unter einer Bewegungsgleichung versteht man eine mathematische Gleichung (oder auch ein Gleichungssystem), die die räumliche und zeitliche Entwicklung eines mechanischen Systems unter Einwirkung äußerer Einflüsse vollständig beschreibt. In der Regel handelt es sich um Systeme von Differentialgleichungen zweiter Ordnung.

Diese Differentialgleichungen sind für viele Systeme nicht analytisch lösbar, sodass man bei der Lösung geeignete Näherungsverfahren anwenden muss.

Prinzipien

Zum Aufstellen von Bewegungsgleichungen in der klassischen Physik wird

verwendet. Darauf basierend ergibt sich die Bewegungsgleichung der Quantenmechanik, die Schrödingergleichung.

In der Technischen Mechanik werden

das Prinzip der virtuellen Arbeit (D’Alembertsches Prinzip)
das Prinzip der virtuellen Leistung (Prinzip von Jourdain)
das Prinzip des kleinsten Zwanges

verwendet.

Lösung

Die Lösung der Bewegungsgleichung ist die Trajektorie, auf der sich das System bewegt. Sie ist, abgesehen von einigen einfachen Fällen (siehe Beispiele unten), meist nicht in analytisch geschlossener Form darstellbar und muss über numerische Methoden gewonnen werden. Dies ist z.B. zur Ermittlung der Trajektorien dreier Himmelskörper, die sich gegenseitig gravitativ anziehen, erforderlich (siehe Dreikörperproblem). Zur Lösung eines N-Teilchensystems lässt sich die discrete element method anwenden. In einfachen Fällen wird die geschlossene Lösung als „Bahngleichung“ bezeichnet.

Beispiele

Eine allgemeine Form der Bewegungsgleichung in der klassischen Physik lautet beispielsweise

${\frac {d{\vec {p}}}{dt}}=\sum _{i}{\vec {F}}_{i}$ .

Oder bekannter:

${\frac {d{\vec {p}}}{dt}}=m\cdot {\vec {a}}=\sum _{i}{\vec {F}}_{i}$

Auf der linken Seite steht der Trägheitsterm für das Teilchen der Masse , auf der rechten Seite werden alle auf das Teilchen wirkenden Kräfte ${\vec F}_{i}$ aufsummiert.

Bewegungsgleichung eines kräftefreien Masseteilchens

Die Bewegungsgleichung lautet in diesem Fall

$m\cdot {\frac {d^{2}{\vec r}(t)}{dt^{2}}}={\vec F}={\vec 0}$

mit:

${\vec F}~$ : Kraft auf Teilchen (= 0),
: Masse des Teilchens, und
${\vec {r}}(t)$ : (zeitabhängiger) Ort des Teilchens

Die Bahn erhält man durch zweimaliges Integrieren der Differentialgleichung:

${\vec r}(t)={\vec v}_{0}\cdot t+{\vec r}_{0}$

mit den Integrationskonstanten:

${\vec v}_{0}$ : Geschwindigkeit des Teilchens zu ,
${\vec r}_{0}$ : Ort des Teilchens zu

Das Teilchen bewegt sich also geradlinig mit konstanter Geschwindigkeit. Die Masse spielt keine Rolle.

Bewegungsgleichung eines Teilchens unter Einfluss einer konstanten Kraft

Ein Körper der Masse sei der Schwerkraft $m{\vec g}$ ausgesetzt:

$m\cdot {\frac {d^{2}{\vec r}(t)}{dt^{2}}}=m\cdot {\vec g}$ .

Die Bahngleichung lautet

${\vec r}(t)={\frac {1}{2}}\cdot {\vec g}\cdot t^{2}+{\vec v}_{0}\cdot t+{\vec r}_{0}$

und stellt den ballistischen Parabelwurf dar. Für ${\vec v}_{0}=0$ erhält man den freien Fall. Im Fall der Schwerkraft spielt die Masse des Körpers also keine Rolle.

Bewegungsgleichung der Speziellen Relativitätstheorie

In der speziellen Relativitätstheorie wird die Viererkraft definiert als die Ableitung des relativistischen Impulses p nach der Eigenzeit $\tau$ , mit

$F^{\mu }={\frac {{\mathrm d}p^{\mu }}{{\mathrm d}\tau }}=\gamma {\frac {{\mathrm d}p^{\mu }}{{\mathrm d}t}}$ ,

wobei zwischen Eigenzeit und der Zeit t der Zusammenhang

$\mathrm d \tau = \frac{1}{\gamma} \mathrm d t$

gilt und $\gamma$ den Lorentzfaktor bezeichnet.

Aus dieser Bewegungsgleichung folgt, dass zwischen den klassischen Größen der räumlichen Kraft $\mathbf F$ und Beschleunigung ${\mathbf a}$ zwar ein linearer Zusammenhang besteht, aber keine einfache Proportionalität mehr: Für Anteile von $\mathbf F$ parallel zur Bewegungsrichtung gilt ${\mathbf F}_{{\|}}=\gamma ^{3}m{\mathbf a}$ , für senkrechte Anteile hingegen ${\mathbf F}_{{\perp }}=\gamma m{\mathbf a}$ .

Bewegungsgleichung der Allgemeinen Relativitätstheorie

Die Bewegung eines Körpers wird durch die Geodätengleichung der gekrümmten Raumzeit beschrieben, sofern nur gravitative Kräfte auf ihn einwirken. Dann bewegt sich der Körper entlang einer Geodäten der Raumzeit. Die Geodätengleichung lautet

${\ddot {x}}^{{\mu }}+\Gamma _{{\lambda \nu }}^{{\mu }}{\dot {x}}^{{\lambda }}{\dot {x}}^{{\nu }}={\ddot {x}}^{{\mu }}+{\frac {g^{{\mu \rho }}}{2}}\left(\partial _{{\lambda }}g_{{\nu \rho }}+\partial _{{\nu }}g_{{\lambda \rho }}-\partial _{{\rho }}g_{{\lambda \nu }}\right){\dot {x}}^{{\lambda }}{\dot {x}}^{{\nu }}=0$

wobei $\Gamma _{{\lambda \nu }}^{{\mu }}$ ein Christoffelsymbol 2. Art ist, welches die Abhängigkeit des metrischen Tensors vom Raumzeitpunkt (Ereignis), d.h. der Krümmung der Raumzeit, charakterisiert.

Bewegungsgleichung in der Strukturdynamik

In der Strukturdynamik ist die Bewegungsgleichung eines dynamisch belasteten Tragwerks die Grundlage der Berechnung:

$M\cdot {\ddot x}(t)+D\cdot {\dot x}(t)+K\cdot x(t)=f(t)$

Hierbei ist f(t) der Lastvektor des Systems. M,D und sind die Masse-, Dämpfungs- und Steifigkeitsmatrizen des Tragwerks. Der Vektor x(t) enthält die Verschiebungsgrößen. Die matrizielle Aufbereitung entsprechend den Freiheitsgraden einer Struktur eignet sich sehr gut für eine Computerberechnung, zum Beispiel nach der Finite-Elemente-Methode.

Quantenmechanisches Kastenpotential

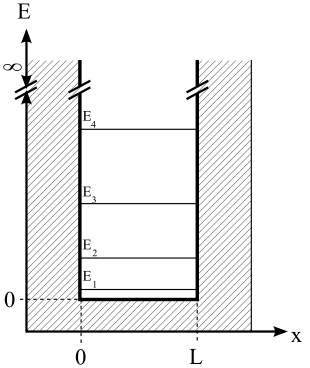
Eindimensionaler Quantentopf der Länge L mit unendlich hohen Wänden. Es sind nur diskrete Energieeigenwerte E_n erlaubt (hier sind lediglich die untersten vier Niveaus E₁ bis E₄ dargestellt).

In der Quantenmechanik tritt die Schrödingergleichung als Bewegungsgleichung auf. Für das einfache Problem des Teilchens im eindimensionalen Kastenpotential der Länge mit unendlich hohen Wänden lautet die zeitunabhängige Schrödingergleichung:

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi (x)+V(x)\psi (x)=E\psi (x)$

mit

$\psi (x)$ : Wellenfunktion des Teilchens
: Kastenpotential $={\begin{cases}0,&{\text{wenn }}0<x<L\\\infty ,&{\text{sonst }}\end{cases}}$ .

Die Energieeigenwerte $E_{n}$ sowie die zugehörigen Eigenfunktionen $\psi _{{n}}(x)$ , $n=1,2,3,\dots ,\infty$ , lauten:

$E_{{n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\cdot n^{2}$

$\psi _{{n}}={\sqrt {{\frac {2}{L}}}}\cdot \sin \left({\frac {n\pi x}{L}}\right)$

Basierend auf einem Artikel in:

Wikipedia.de